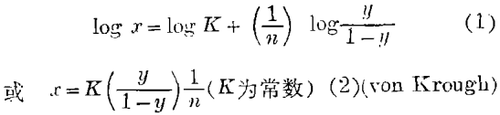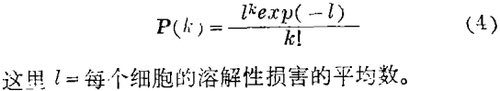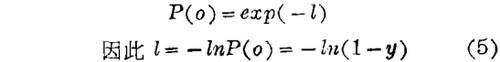古代的人们已经知道了天花的免疫现象,甚至进行着危险的免疫操作。约1800年琴纳成功地发展了种痘技术。然而,琴纳的发现在将近100年的长时间内对了解和治疗其他疾病并未发生影响。这正如埃尔利希指出的:“琴纳的发现所以是孤立的,原因是关于传染病的原因和本质的理论概念未发展的缘故。”
本世纪以来,免疫学发展起来了,各种理论的论争主宰了免疫学领域。本文将对主要的非数学性学说、对免疫测定、免疫系统的数学模型作简短的历史性评述。
主要的非数学性学说
一、抗体形成的指令学说和选择学说
可以把众多的免疫学说分成选择学说和指令学说两大类。选择学说认为抗体选择性地刺激预先存在的互补的抗体。指令学说认为抗体指令动物怎样去产生原先不存在的互补抗体。
早期的选择学说模型提出者——埃尔利希,认为每个应答细胞都有多样的表面受体(用现代术语表述)可与各种抗原互补。应答细胞与抗体的接触刺激了细胞大量合成特殊的与抗原互补的受体,并释入循环成为抗体。1920年以后,免疫学家们开始放弃埃尔利希的模型,因为预先存在着这种多样性,尤其在单个细胞上,是难以理解的。尽管埃尔利希模型已被认为是不正确的,但是在抗原刺激之前预先存在着多样性,现今却得到了普遍的承认。
三十年代时期,许多免疫学家相信抗原必然是教导抗体形成机制怎样去产生互补的抗体。鲍林(1940)提出了明确的指令模型。他指出,一切抗体都有共同的氨基酸链,但它们的三维构型的末端则由直接接触的抗原模板来规定它们的合成。而且,抗体与抗原分子分离以后,抗体的构型仍然能保持稳定。鲍林的学说虽然可以解释无限多的抗体构型,但是未能深入免疫记忆的本质。况且,进一步发现抗体的构型像其他蛋白一样是由抗体本身的氨基酸链来决定的。
杰恩(Jerne,N. K.)(1955)重新提出选择学说,他认为:在发育过程中,即使无抗原存在,也产生多种多样的自然抗体。抗原有选择地与循环着的互补抗体结合。抗原 - 抗体的复合物被免疫吞噬细胞吞噬后,即刺激吞噬细胞或其他细胞大量地产生相同特异性的抗体。
1957年伯奈特(Burnet,F. M. )及塔尔玛杰(Talmage,D. W. )作出了关键性的假设:每一种应答细胞只在它的表面上制造和表现出一种抗体分子,选择性事件只是抗原对那些互补抗体的制造进行刺激,从而引起这些细胞的增殖并分泌抗体。这便是伯奈特的无性系细胞选择学说。
二、抗体多样性的根源:体细胞突变学说与胚系学说,自我与非自我识别
抗体分子的多样性来自其氨基酸链的多样性。现在知道抗体分子由二条200多个氨基酸的轻肽链和二条400多个氨基酸的重肽链组成。在分子的一端各条链的末段是由约100个氨基酸组成的高度可变性的终端,其可变性集中于3 ~ 4个高度可变性区,在这里形成抗原的结合位。
解释抗原产生的多样性可有两种对立的学说。胚系学说认为,对于每一种可变的氨基酸序列,在胚系中均有相应的DNA序列。这些“基因”是进化和自然选择产生的。另一种体细胞突变学说认为,多样性来自个体细胞发生或淋巴细胞分化时的体细胞突变(或其他随机过程)。
然而,不论哪种学说均必须解释抗体不对抗自体成分这个问题。
伯奈特在他的无性系细胞选择学说中假设:抗体产生的多样性来自胎儿时期体细胞突变的随机过程,因此出生后抗体与抗原的结合部位便是固定数量的了。他还进一步假设任何淋巴细胞处于产生多样性的敏感时期时,一旦再认了自体(或异体)抗原,其自身即死亡消除。莱得勃格(Lederberg,J. )(1959)对伯奈特的无性系细胞选择学说进行修正,认为体细胞突变在动物一生中不断地产生新的无性系细胞,每一株无性系细胞均经过一敏感阶段,这时若接触自体抗原即被消灭。总之,正常成体动物不应发现自体反应性无性系细胞。
1971杰恩假设能够识别自体的无性系细胞在原始淋巴样器官,如胸腺中增生和突变,未突变的肉体反应性细胞在接触自体抗原后即被杀灭,突变的细胞则存留了下来。后来,杰恩进一步考虑抗体分子本身的自体抗原对生成多样性和调节免疫反应的影响后,提出了网络学说。
六十年代,免疫学家发现动物对抗原暴露后,根据抗原给予的具体情况的不同或者无反应(耐受)或者免疫,这提示成熟淋巴细胞接触抗原后或受刺激或被麻痹。据这些,伯莱切尔(Bretcher,P)和科恩(Cohn,M)(1970)提出了“两次信号学说”,他们认为当暴露于互补的抗原后,自体反应性细胞被麻痹,无自体反应性细胞则受刺激。抗原与淋巴细胞的接触总是给淋巴细胞麻痹性信号,刺激或诱导则'品要第二次信号。第二次信号必须是抗原特异性的,而且是来自第二个细胞或来自第二个抗原识别细胞的可扩散性因子。这个模型认为抗原反应性细胞不停地生成,自体与非自体抗原的区别则是因为自体抗原是始终存在着的(至少在反应细胞生成时存在着),而非自体抗原只是第一次出现的。当具有自体抗原实体的细胞生成时,它们是一个一个与抗原接触的,这时没存任何助因子或细胞给出第二次信号,于是这些细胞将全部被麻痹。异体抗原原先因为并不存在,在这段时间中已积累了一定数量的助细胞或助因子。因此,当抗原被引入并与反应细胞相遇后,因已有足够量的助细胞或助因子,于是引起强烈的第二次信号或诱导。晚近,伯莱切尔(1974)用第二次信号学说来解释细胞介导性免疫和体液免疫的控制,IgM(免疫球蛋白M)至IgG的转换。当动物第一次遭遇危险的抗原时,它必须以最有效的方式进行反应,即应用细胞介导免疫系统,以后再依次转换成IgM和IgG反应,以便将对自体的损害减至最小。
数学性的学说
免疫学中有许多数量性的问题,解决这些问题需要应用数学分析或数学模型。
一、测定和实验操作的模型
1. 补体:敏感红细胞溶解数与补体加入量的关系呈S线曲线。若logx表示补体加入量的对数,logx与log[y/(1-y))] 的关系曲线为斜率为1/n的直线,y为溶解的红细胞的百分率,即
冯 · 克罗(von Krough)公式解释了溶血的S形曲线。伯罗克斯(Brooks)(1919)指出:由于红细胞敏感性的差异,有些红细胞可能需要更多的补体。这就提出了累积损害概念。阿伯弟(Alberty,R. A)和鲍温(Baldwin,R. L. A)(1951)引申了累积损害概念后提出:溶血作用是“多作用现象”(multiple hit phenomenon),应用概率效应也可以解释S形曲线。他们假定一切红细胞是相同的,若每一红细胞含有m基质区与抗体和补体作用,当反应区达到临界值r时出现溶血,溶血细胞的百分数可用二项式布计出:
阿伯弟 - 鲍温的理论与实验滴定数据和冯 · 克罗公式是一致的。迈尔(Mayer,M. M. )(1961)发现当红细胞总数不同时,与阿伯弟 - 鲍温学说的某些不一致现象。例如通常的细胞浓度时(6.7×106个细胞/ml)冯 · 克罗方程的1/n值约为0.2,相对应的阿 - 鲍学说的r=10,而当细胞数为2×109/ml时1/n≈0.43则需要r=2才合适。迈尔(1961)提出一次作用学说,认为一次随机的、临界的事件即足以使细胞溶解。现在已经知道临界事件即一个IgM分子或一对IgG分子在红细胞表面的结合及继之的所有补体成分的结合。根据一次作用学说,平均每个细胞具有K数溶解性损害的细胞比例数可用泊松分布给出,即
各方面的观测证明了迈尔的一次作用说。例如方程式(4)指出每个细胞的溶解性损害平均数可以通过检查未溶解的细胞算出,即
y=溶解细胞的百分数。电子显微镜观测每个细胞上的损害数大都能符合一次作用说。
另外,普鲁特(Pruitt,K. M. )等(1974)提出了补体介导溶血的动力学说。
2. 杰恩溶血蚀斑试验
杰恩琼脂溶血蚀斑试验可用来鉴定抗体分泌细胞,也可用以了解抗体分泌率的情况。典型的蚀斑实验是将预先经羊红细胞或半抗原作用过的羊红细胞免疫的鼠脾的淋巴样细胞与羊红细胞(抗原)混合,平布于琼脂薄层,并37°C孵育1 ~ 2小时。在孵育前或后加入补体,使红细胞溶解,因此在抗体分泌细胞周围形成溶血蚀斑。
根据弥散反应方程式已作出了蚀斑试验的数学模型。该模型假设抗体生成细胞以恒定的速率各向相同地分泌抗体。这些抗体以恒定的弥散系数D与均匀分布的红细胞结合。假定红细胞和抗体形成细胞的大小可不计。在位置r的游离抗体浓度C(r,t)服从下列方程式:
这里,ρ0为与抗体结合的红细胞部位的总浓度,方程式(7),(8)形式的弥散反应方程式曾用来分析抗血清由圆坑向薄度凝胶的弥散。
3. 抗体亲和力的分布:抗体的亲和力即单个抗体部位与单个抗原附着素的结合平衡常数。根据质量作用方程,在平衡时每分子抗体与半抗原的结合数γ,对于同种抗血清,可由下式给出:
二、细胞与抗原相互作用模型及群体层次免疫应答模型
对于多价抗原与细胞受体的动态结合,贝尔和德里西(1974)根据可逆双分子可逆反应的质量作用定律,提出了简单的数学模型。后来,贝尔(1974)又根据多价抗原与细胞结合的二步机制修改了他的模型。贝尔认为抗原分子首先与单一的受体部位结合,然后解离或与其他受体分子以不可逆的形式形成多价结合。一分子抗原与单体IgM或IgD细胞受体分子的两个部位的结合,称为一一对应的双价性。克罗塞斯(Crothers,D. M. )及麦茨格(Metzger,H. )(1972)对这种现象作了平衡统计力学的研究。
如果多价的配位基是长链状的分子,开始时为一点的微弱结合(成核作用),紧随着剩余配合基的进行性结合,“拉链”模型是有价值的。拉链模型曾用来解释核酸的双螺旋形成,并用来解释激素与细胞受体的结合。
有许多学者对体液免疫反应进行了研究。吉力克(Jilek,M. )(1973)对免疫反应的动力学提出了随机模型。科恩(1971)对抗体生成和耐受的诱导提出了模型。他认为一个抗原分子与单一受体结合是激活信号,而二个抗原分子与两个邻近的受体结合则是抑制性信号。贝尔(1970,1971)认为抗原与细胞受体的相互作用服从质量作用定律并假设靶细胞因部分受体部位被结合或交叉连接而受到激活、而当靶细胞的全部实体部位被占据时则大部分被杀灭。贝尔认为,靶细胞群体分成对抗原具有不同亲和力的次群体,当靶细胞受到抗原刺激后,变成增殖细胞,分泌抗体并进一步分化成记忆细胞或浆细胞。浆细胞与增殖细胞也分泌与其来源的靶细胞相同亲和力的抗体。贝尔的模型已经作出微分方程。布隆尼(Bruni,C. )等(1975)对抗原抗体结合提出了与贝尔模型类似的积分差分方程式模型。
一些群体层次的模型均涉及对淋巴细胞刺激机制及淋巴细胞向增殖细胞转变或分化成浆细胞或记忆细胞的控制决定过程。许多研究者均企图对这些过程作出正确的描述。华尔特曼(Waltman,P. E. )及布兹(Butz,E)(1977)把淋巴细胞的刺激和对增殖细胞分化成浆细胞的决定看作为阈值现象,并提出了动态模型。梅里尔(Merrill,s. )(1977)吸收汤姆(Thom)最近的灾变学说的思想提出了B - 细胞刺激和原发免疫反应的模型。佩雷尔松(Perelson,A)等(1976,1977)利用最优控制学说的思想决定B淋巴细胞增殖和分化的最佳形式以便以最优化的方式去除抗原。关于免疫反应控制的数学模型已根据杰恩的网络学说作出。
在群体水平上,贝尔(1973)提出了捕食者与被捕食者模型。杜宾(Dubin,N. )应用非线性的生死过程对肿瘤生长的免疫反馈作出了模型。莱菲弗(Lefevev),和加雷(Garay)提出了免疫监察的数学模型。
(Bell,G. I.等Theoretical Immunology,3 ~ 41页)