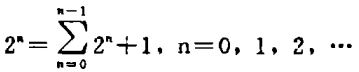笔者根据现代数学中的代数学、几何学与数论的理论和方法,完成了对《河图》、《洛书》和《易卦》三大符号体系的初步数学研究,建立了对河图和洛书的数学分析,洛书矩阵学说,洛书数字几何学,及周易宇宙代数学。根据这些初步研究成果,笔者就可描绘出这三大古老符号体系的现代数学结构,示出三者间的演进机构和过程,建立三者所组成的具有连续性、自洽性与整体性的“河洛易数学体系”。
一、河图的数学结构与由河图到洛书
1. 河图的数学结构
河图代表中国古代人民由北京人到伏羲时代的数学思维的结晶模型,它是人类根据宇宙本身内在的自然数系、界定出来的数学思维的基础符号体系。在人类文化史中,中国人首先制定并采用十进位数系,他们根据对人类双手十指的结构和宇宙间各种事物现象的长期体验,就创造了用十进位数系来描绘事物间的数量关系;并在应用十进位数系的体验中,创造了《河图》、《洛书》和《易卦》三大数学思维符号体系。
用现代数论语言来说,河图所用的数集可表为H={1,2,3,4,5,6,7,8,9,10},它的数学结构是由五个序偶(x,y)和(a,b)按照泛函关系y=f(x)=x+5所组成。此即河图结构关系式:Rh={(x,y);y=x+5;x,y∈H}={(1,6);(2,7);(3,8);(4,9);(5,10)}。
因为河图内的序偶都是二元数,根据矢量代数学的解析,我们亦可证明河图数字能够张成一个2维的矢量空间。
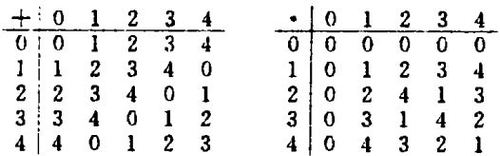
数学是数与形的结合,河图图形的排列亦必有其数学机理。河图的中心数字是5,象徵为十进位数系中的枢纽数(pivotenumbers)、中数(meanvalne)或模数(module)。环绕核心5及其四周的五个序偶就是河图的元始定义,谓:“一与六共宗,二与七为朋,三与八成友,四与九同道,五与五相守”。这个原始定义的数学意义,就是河图图形排列的机理,亦就是以模数为5的同余算术及其所生出的五个等价组如下 :
0≡0(mod5)5≡5(mod5)10≡0(mod5)(河图核心)
1≡1(mod5)6≡6(mod5)(河图下方)
2≡2(mod5)7≡7(mod5)(河图右方)
3≡3(mod5)8≡8(mod5)(河图左方)
4≡4(mod5)9≡9(mod5)(河图上方)
这即表示出在整数系中,每个整数可分别相当于0,1,2,3或4。
这五个等价组的加法符合a(mod5)+b(mod5)=(a+b)(mod5),乘法符合a(mod5)·b(mod5)=a·b(mod5),其加法表与乘法表分别示出二法所生的逆数如下:
根据上面的数论解析,我们可以得出一个推论 :河图的数字结构显示出十进位数系的操作二重性特质。它既可按照线性关系由核心扩张为连续性与无限性的宇宙二维空间,亦可按照同余关系聚集为间隔性的等价组合和有限(有定)性的二维空间,这就是宇宙空间的二重性特质。
2. 由河图到洛书
宇宙空间形成的过程是由一维的直线系统扩张成为二维平面系统,再进而成三维空间系统,再进而成四维时空系统。每一系统的构成必有它的数域基础,每两个系统间的转变必遵循一定的转变函数关系。整个宇宙空间就构成一个相关的、自洽的和整体性的数学体系。河图代表二维平面体系,构成河图序偶(x,y)或(a,b)的泛函关系为y=x+5,如果吾人已知洛书代表三维空间体系,它的三元数序为(x,y,z)或(a,b,c),三元数的泛函关系为x+y+z=15,则由河图到洛书的转换示如表1。
表1. 由河图到洛书
[表1示出由河图中的四个序偶所生出的四个对应的洛书三元数。但吾人仍采用枢纽数5为洛书的中心时,则合乎x+y+z=15泛函关系者尚有三元数(1,5,9);(2,5,8);(3,5,7);(4,5,6)。吾人将此二组三元数结合成为一个体系,就是洛书。]
二、洛书的数学结构与由洛书到易数
1. 洛书的数学结构
洛书代表中国古代人民由伏羲到夏禹时代的数字思维的结晶模型。在这约有千年的历史过程中,中国人民将代表二维平面空间数系的河图演进,并升华为代表三维立体空间的洛书三元数系。洛书九数的原始定义就是“二九四,七五三,六一八”。按照洛书九数龟形排列的形状,定义洛书为“九宫”曰:“九宫者,即二四为肩,六八为足,左三右七,载九履一,五居中央”。又因洛书中每行、每列及两对角线所成三元数字的和均为15,中国及世界的数学家们就称洛书为“幻方”,并建立和发展出“幻方数学”,直到今日。作者为了将“洛书幻方”与现代数学挂钩,就根据现代数论、代数学及几何学对洛书的数学结构进行研究,现将主要结论概述如下。
根据现代数论,洛书所用的数集可表为L={1,2,3,4,5,6,7,8,9},它的数学结构是由三个三元数(x,y,z)或(a,b,c)按照泛函关系x+y+z=15组成,,此即洛书结构关系式:Ri={(x,y,z):x+y+z=15;x,y,z∈L}={(4,9,2);(3,5,7);(8,1,6)}={(4,3,8);(9,5,1);(2,7,6)}。根据洛书数的集运算,吾人可以建立多种的数字系统与结构。(见本刊1992年第8、9期)
根据矩阵代数学,笔者就将“洛书幻方”直接等同为“洛书矩阵”,建立了焦氏“洛书矩阵”学说(刊载于本刊1987年第3期)。
根据解析几何学,笔者应用洛书矩阵中三行或三列三元数系作为三维坐标系统中的三个基矢,以代替解析几何中所用的卡氏(Cartesian)单元基矢,就可建立一个新的解析几何系统,作者称它为“洛书数字几何学”。(全文刊载于本刊1991年第3期)
2. 由洛书到易数
由洛书三元数系(a,b,c)到易数E=x+iy的建立,绝不是简单直接的由算术的加、减、乘、除操作所产生,而是长期人类数学思维的成果结晶。具体地历史证明,就是由夏、禹王时代的洛书符号体系发展为周文王时代的易卦阴阳符号体系。作者根据现代数学理论,说明由洛书到易数的数学转变过程如下:
5.1.3
表2. 洛书三元数序所生实数序列与虚数序列
三、易卦的数学结构与由易卦到太极图
1. 易卦的数学结构
笔者根据易卦阴阳符号体系和复数域的相互对应关系,奠定了易卦即易数,易数即复数;并建立了焦氏“周易宇宙代数学”。(见本刊1993年第5,11,12期)易卦(数)体系的主要特质之一是其阴(实)阳(虚)二重性,亦即易数(Zn)体系是一个实数(Xrc)和虚数(Xim)二的二重性集合,表作
在Z3中n=3,共含23=8卦,卦序由坤为第一卦到乾为第八卦,其中坤与乾、艮与兑、坎与离、巽与震互为二重性,符合x+y=23-1=7之关系。
笔者根据对六爻易卦(数)矩阵的数字解析,可归纳出周易复数空间的两大构成原理如下:
(a)易卦(数)阴(实)阳(虚)二重性的整体性原理:六爻卦系复数矩阵[Zkj]8×8是由其实数矩阵[Xkj]8×8和虚数矩阵i[Ykj]8×8相加而成,实虚两部的组成元素是由相同的自然数集按照相反的升降序列组成,所以易数集构成一个有序的、可数的无穷复数系统,作者称易数构成关系式(|x|+|y|)n=2n-1曰“易数实虚二重性整体"原理。如此吾人可推导出易数集与实数集的相互对应关系有:(i)自然数集是构成实数域的基础子集,易数集是构成复数域的基础子集。(ii)自然数集的算术运算、衍生出实数体系,易数集的算术运算、衍生出复数体系,(iii)实数只能位于实数线上,点与数可互为置换;易数只能位于乾坤线上,点与数可互为置换。
(b)周易复数空间的线性结构原理:易数之值是按照二进制爻位系数规则而定,此易卦爻序中,第n位爻符之系数值等于其余所有各位爻符之系数值之和加1,即
作者称此式曰“易数线性结构”原理同样,易卦矩阵[C]并非下卦矩阵[A]与上卦矩阵[B]的乘积,而是[A]与[B]的线性组合,符合线性方程式[C]=m[A]+[B],m之值即由二进制爻位系数定则决定。在三爻八卦体系中,下卦A为二仪,上卦B为四象。其线性组合式为(C)=2(A)+(B),例如坤卦为(7,0)=2,(3,0)+(1,0);坎卦为(5,2)=2(2,1)+(1,0)。六爻卦系为八卦相互组合而成,按照易数空间的线性结构原理,可定出其线性公式为C=8(A)+(B),例如恒卦(35+28i)的下卦为巽(4=3i),上卦为震(3+4i)?符合线性关系:(35+28i)=8(4+3i)+(3+4i)。读者可求出64卦中,每卦均符合此关系式。总之,任一易数均符合一般线性组合公式C=m A+n B,再用对应系数法定出m与n之值,完全符合易数空间线性结构原理。
2. 太极图的数学结构分析
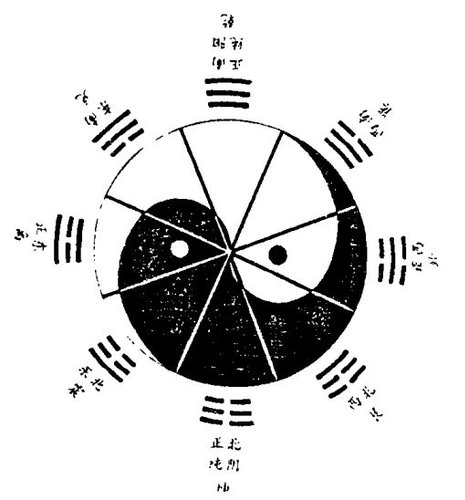
《周易》中只有“太极”一词,并无太极图像。“易”以太极为中心、为建元,其主旨是“乾坤-太极”。太极是道、是本体。易文曰:“一阴一阳之谓道。”但太极如何生出“太极图”?及太极图形象如何?因史无文献可稽,难作论断。太极图形最先出现于东汉魏伯阳所著《周易参同契》中,流传民间,俗称“阴阳鱼”(图1)。宋朝朱熹将此图载入《周易本义》,遂为学者沿用至今,作者现以参同契太极图形为准,分析其数学结构如下:
图1:《参同契》太极图
参同契太极图实际上由下列几条曲线构成。
(a)圆周。其度量单位为360度(2π弧度)。圆的单位半径为r(单位圆),r可任意放大或收缩(例如r=1,10,100……)。
(b)将圆划分为黑白两部分的两条曲线——此处称它为“太极线”。(一般作者称它为“S曲线”)。
在有些著作中,曾将该两条曲线当作两个半圆来处理,但由图中可以看出,半圆曲线与太极曲线的误差甚大,而且半圆曲线也缺少太极的“无穷演化”的特质。为此,作者建议用等速螺线来比拟太极曲线。等速螺线的定义为:一质点以等速离开0点又以等角速度绕0点旋转,该质点所描绘的轨迹为一等速螺线,由此得两条等速螺线的数学方程(极坐标)为:
阴线:r=aθ (θ=0~π)
阳线:r'=a(θ'-π) (θ'=π~2π)
当θ=π r=0 得a=10/π
(c)极点。太极图中黑白两部分中各有一个“眼”。亦即数学上的极点。其意义相当于球体的南北极,或是流场中的“源”与“汇”。如将太极图当作极坐标内的平面图形。则可得到两极点的坐标约为:
阳极点:r1=4,θ1=(5/8)π
阴极点:r2=4,θ2=1(5/8)π
3. 从河洛数集到太极图(暂略)
4. 由易卦到太极图(暂略)
四、河洛易数学体系结论
河洛易数学体系是以《洛图》、《洛书》和《易卦》三大符号体系为构成它所建立的数学体系,它是中国古代人民由北京人到孔子数十万年间数学思维结晶而成的符号体系,吾人可称它为“中国原始思维数学符号体系”;它是中国原始传统文化建立和成长的数学基础。作者根据对这三大符号体系的数学内涵之研究,及对三者间数学转换的解析,就可归纳出河洛易数学体系的主要结构和特质如下。
1. 它是根据人类双手十指的数学模式而建立的。
2. 它是根据宇宙本体所具有的自然数集V= {0,1,2,3,4,5,6,7,8,9}及其算术操作(加、减、乘、除)而建立的十进制数学系统。
3. 它是以天、地、人三才的有机结合产1出三者所含象、数、理的互释,再进而衍生出人类文化中的各种信息与系统的数学体系。
4. 由伏羲时代的河图符号体系到周文王时代的易卦阴阳符号体系的发展,就是人类将数系由自然数集衍生为复数集的数学思维的发展。
5. 河图符号体系代表宇宙中二维矢量空间的形成,它是准照线性函数f(n)=a+nd所张成的连续性无限空间;换句话说,河图数集就是算术级数的集合,函数式中的d=5为公差,其中a为级数的首项,可分别为自然数集的形成基数0,1,2,3和4。
6. 河图的结构是由核心及其四周的5个序偶组成,它的数学意义就是整数集可按照模数为5的同余数学区分成5个等价组合,示出整数集中每个整数可分别相当于0,1,2,3或4。
7. 洛书数集是数系中的基础,可用它建立多种的数字系统与结构。
8. 洛书幻方的结构可直接等同于洛书矩阵,张成为三维矢量空间,洛书矩阵就是自然界中线性系统的建立基础。
9. 洛书空间具有一些特质,可以描绘自然界中的客观现象及显示物理世界量子化的映像,这些特质都非一般几何空间所能显示。
10. 易卦阴阳符号体系的建立标志着人类数学思维的一大跃进,就是将实数域中的十进位数系精简为阴阳两爻的二进位数系。
11. 易卦阴阳符号体系和现代数学中的复数系统互有一一对应关系,这就奠定了易卦就是易数,易数就是复数。
12. 易卦复数空间具有两大数学特质:一为易卦(数)阴(实)阳(虚)二重性的整体性原理;一为易数空间符合线性结构原理。
13. 河图、洛书与易卦三大符号体系可以通过数学操作与太极图的图像之间实行相互转换。这种转换过程也体现了现代科学中的模(Modele),数(Number)与象(Phenomena)之间的相互转换。
14. 河图、洛书和易卦三大符号体系,其数学、科学与哲学内涵就是人类文化之构成的主要思维内涵。
最后,且以摘语四句作为本文的结束语。
五年纵横显河图,三维矩阵谱洛书,
两仪阴阳启易卦,太极万象化时空。
(本文是焦蔚芳博士专著《周易宇宙代数学——河洛易数学体系》中的一章,本刊发表时作了删节,该专著汇总了焦博士近十余年来的研究成果,集中反映了作者的以数学为焦点,实现中西文化融合的创见,以及作者为推动中华民族在21世纪于更高的层次上发扬光大所作的努力。该专著将于今年三季度由上海科学技术文献出版社出版。有兴趣的读者可与本刊联系邮购。)