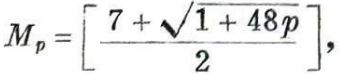[提要]“四色问题”是指这样一个猜想,即在平面或球面上画地图,只需要四种颜色,就可以使得相邻两国不用同一色。要证明这个问题很难。19世纪中叶提出来以后,著名英国数学家凯利曾热心呼吁解决。但是经过了100多年来的努力,还是证明不了。直到1976年才由美国数学家阿佩尔和黑肯利用电子计算机证明了,使数学界轰动一时。他们看到证明这个猜想并不是不可能,只是证明的步骤、程序很复杂,人一辈子的时间也不够用。阿佩尔和黑肯就把程序编好,交给高速的电子计算机去干。电子计算机也花了1200小时才证了出来。
四色定理本身没有什么突出的理论价值和实用价值,因而他们的主要贡献也不在于证明了四色定理,而是用电子计算机解决了人们一个多世纪以来所一直未能解决的一个纯理论问题。这说明,靠人机合作就有可能完成许多连最著名的数学家至今也束手无策的任务。因此,这个做法本身标志着人类认识能力的一个新飞跃,体现了人类的无限潜力——他们能够用自己的手和脑创造出一些使他们的手和脑本身得到了无限加强的东西。
本文原载苏联《自然》杂志,1977年6月号。作者是苏联国立雅罗斯拉夫大学物理-数学科学博士。
我面前放着一封从美国伊利诺斯州一座不大的大学城厄巴纳寄来的信。标准的白色信封上盖了个不寻常的邮戳:即所谓邮票特种注销邮戳,这种邮戳只是在人们想庆祝什么著名事件时才使用的。邮戳上的铭文是:“four colours suffice”(“四种颜色就够了”)。
“地图着色问题”通常与十九世纪最伟大的几何学家之一A · F · 默比乌斯的名字有关。默比乌斯的许多思想只是在许多年之后才得到真正的评价,他可以算是拓扑学的创始人之一,直到本世纪,拓扑学才发展成一门重要的科学。
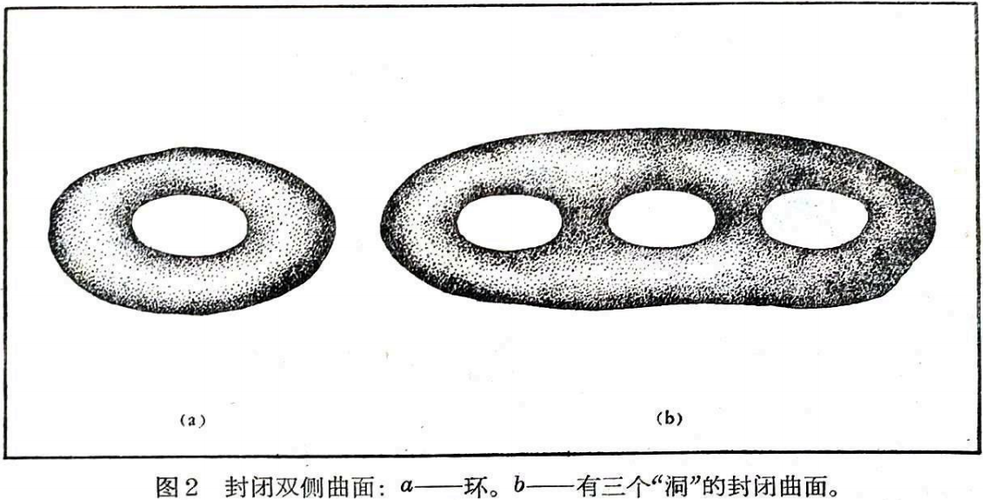
拓扑学是研究图形在任何连续变形情况下,譬如说,任意弯曲和拉伸画在橡皮薄膜上的图形的情况下,都保持的最一般的特性。默比乌斯对拓扑学最有名的贡献是发现所谓单侧曲面,其范例就是著名的默比乌斯带;但默比乌斯带并不是唯一的例子。1840年,默比乌斯叫自己的学生们注意,在平面上很容易指出四个区域,其中每两个区域都有一个公共的边界(而不是只有一个公共边界点),并建议他们证明,在平面上决计不可能指出五个区域都具有上述特性。从这个论断的证明中(证明是相当简单的!)得出脍炙人口的默比乌斯假设:画在平面或球面(地球仪)①上的每张地图都可以用四种颜色着色,使得有公共边界的每两个国家都可用不同的颜色来着色。这个假设后来叫做“四色假设”,而证明(或推翻)它的任务就叫做“四色问题”。
默比乌斯提出四色假设十年之后——约在1850年到1852年间——英国人弗兰西斯 · 格思里由于英国地图合理着色的实际任务而碰到了四色问题,因为在地图上着色时每个郡都要用一定的颜色;他企图证明四色假设,但是没有成功。在英文文献中,四色问题至今还常称之为格思里问题。
弗兰西斯 · 格思里的弟弟弗雷德里克于1852年10月向剑桥大学教授奥古斯塔斯 · 德 · 摩根谈了这个问题,德。摩根是乔治 · 布尔的战友,以在数理逻辑领域内的研究而知名。德 · 摩根在数学家中间广泛宣传了四色问题。但是四色问题所以真正“世界闻名”,是与十九世纪下半叶最有声望的英国数学家阿瑟 · 凯利(1821~1895)的名字分不开的。
1878年,凯利在伦敦数学会会议上就四色问题作了报告,他在报告结尾轻率地建议与会者独立地解决这个问题。凯利的这个建议真是闯下了祸,因为自他报告以后,各国所有数学中心和全世界所有主要数学杂志都源源不断地收到关于四色假设的种种错误证明。四色问题的大量证明在很大程度上是这样刺激起来的,即确认“任何平面或球面地图都可以用五种颜色来着色”的五色定理无需花什么力气,因为任何学生都能理解有关的证明。
凯利报告之后不久便发表了四色假设的第一批“证明”(A · B · 肯普,1879和P · J · 台特,1880)。凯利和大多数其他数学家(例如著名的F · 克莱因)对有关论证都十分满意。但是在1890年,英国数学家P · J · 希伍德在肯普和台特的论证中发现了错误,这些错误无论怎样也消除不了。
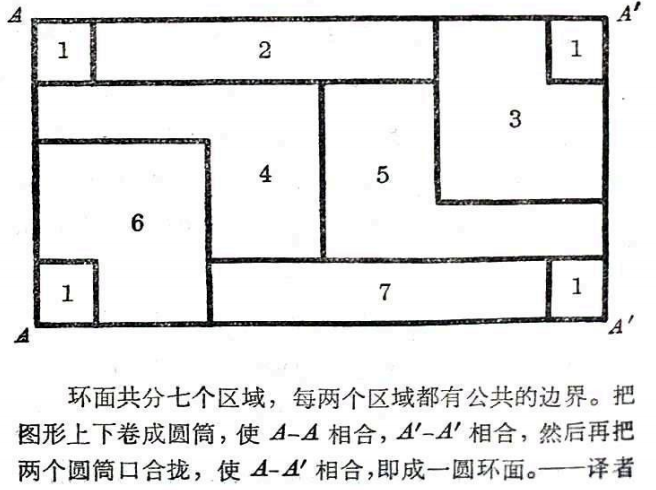
顺便说说,希伍德还开创了一个和四色问题有关的方面。这个产生较晚的方面所取得的决定性的成就要比在该基本问题中所取得的成就更快,也更简单。希伍德是第一个完整解决着色问题的,但是这种解决不适用于平面或球面,只适用于更复杂的曲面。就是说,他证明在环面上(如在土星光环上)解决着色问题要比在地球上简单。在这种情况下,足以为任何地图着色的最小色数等于七。更确切些说,希伍德证明每张环面地图都可以用七种颜色着色,以致任何两个邻国都不会染上同一种颜色。另一方面,既然在环面上可以指出这样一张七国地图,使地图上每个国家和其他任何一国都有公共边界,那么很明显,少于七种颜色就不可能为某些环面地图着色②。希伍德还推测,在有p≥1个“洞”的封闭曲面上,足以为任何地图着色的最小色数等于
这里方括号表示所括数的整数部分。显然,当p=1时(环面情况)这个数M?等于7。
近年来,希伍德的这个假设首先受到了德国数学家G · 林格尔和美国数学家U · T · 扬斯的系统攻击。林格尔证明,在任何(双侧的或单侧的)不同于球面的封闭曲面上,足以为任何地图着色的最小色数是与这样一种地图上的最大可能的国家数相符的,在这种地图上,每个国家和任何其他国家都有共同的边界。此地要特地声明所研究的曲面不同于球面,这意味着从着色问题的观点看来,我们的地球和我们所知道的其他一切行星(就除了我们上面提到过的土星光环以外)是安排得最不利的!林格尔用这个假设首先证明了,足以为任何一张有p≥1个“洞”的封闭(双侧)曲面地图着色的真正最小色数Np永远也不会超过“希伍德数”Mp,且与Mp之差不会大于2。后来扬斯甚至证明Np与Mp之差不会大于1,而希伍德的假设对于不同于球面的“几乎一切”封闭曲面都是成立的,这里“几乎一切”一语可以赋予某种严格的意义。最后,林格尔正是根据上述一系列工作证明希伍德的假设对于所有不同于球面的(封闭双侧)曲面毫无例外都是正确的。林格尔在1974年出版了第二本书(《地图颜色定理》)来纪念于1970年逝世的扬斯,书中清晰地叙述了这个问题的历史,并对希伍德的假设作了完整的证明。
林格尔 - 扬斯的研究完全解决了“古怪的”(“有洞的”甚至是单侧的)行星地图的着色问题。这样就只(!)剩下原来那个地球上的(和平面上的)地图着色问题没有解决了。而且近数十年来,所有解决“着色问题”的著作(包括与希伍德问题有关的一系列著作)都是以图论为根据的,而且都是以这一问题的下列另一种说法为根据的。
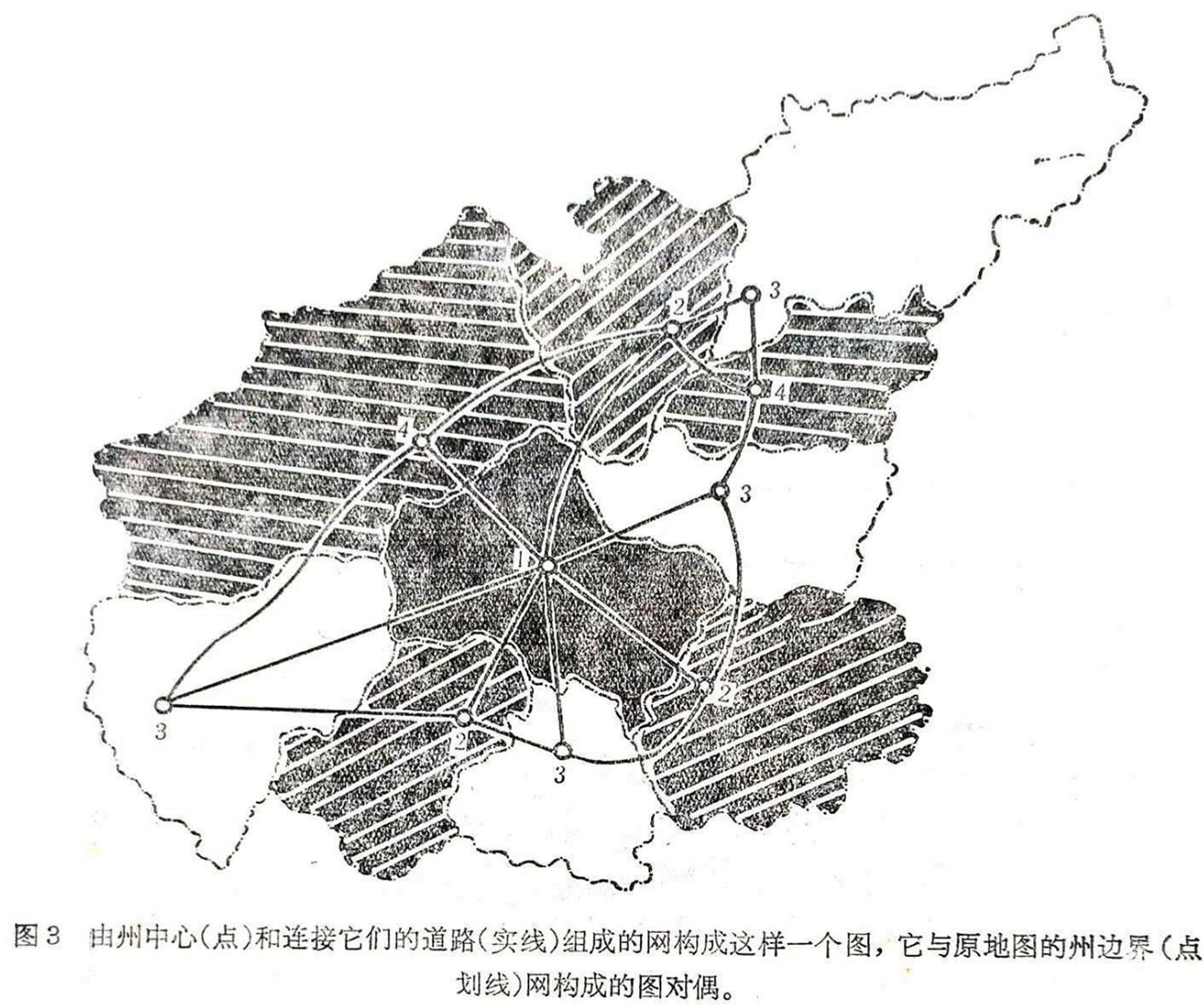
我们假定地图上所有的国家内部选一个点——相应国家的“首都”。我们约定,只有当两个国家有共同边界时,用一条铁路把两国首都连接起来,并让这条铁路通过这段边界。这时由“首都”和连接它们的铁路组成的“网”构成一个图,人们把这个图叫做由原来地图上的国家边界网构成的图的对偶。地图上各国的颜色产生出对偶图顶点的“颜色”(或编号,这里每个编号都表示某种颜色);这种着色法(命数法)在下列意义上是正确的:该图的任何两个“相邻的”(即用一条边连接起来的)顶点可着上不同的颜色(即编上不同的号码)。足以为图的所有顶点“正确”编号的最少号码个数叫做图的色数。这样一来,“着色问题”就被归结为对平面图、球面图或任意曲面图的色数评价问题。就是说,几乎所有与默比乌斯-格思里问题有关的文献都是针对这一问题的。这样一来,五色定理从许多方面都得到了加强。无论从哪个方面来看,所有的定理都处于这种简单的五色定理与难以解决的四色问题之间的中间位置。
近数十年来,对四色问题的进攻多半是以肯普的1879年错误著作的思想为依据的。肯普想找到地图(或图)的某种标准系统,在这个系统中每张图都含有这个系统的一部分;另一方面,所有被研究的配置形式都不应当与四色假设相矛盾(肯普制定了某种标准程序来确定这一点)。后来,许多作者就是根据肯普提出的思想框框去进行研究的。例如,其中就包括俄国读者通过许多译著而熟知的美国学者G · 伯克霍夫;还有且 · 希什,他于1969年出版了一本关于四色问题的书(《四色问题研究》)。希什书的特点在于,作者广泛运用电子计算机来分析四色问题中所出现的许多组合图式。
使用电子计算机来进行分析非常重要,因为必要的分析极为繁杂,需要单独加以考虑的情况数目又极庞大,从而把企图实现肯普思想的所有研究者都引进了死胡同。
早在1971年10月,数学家中间就首次传来了一个耸人听闻的消息:四色问题“好像已经用电子计算机解决了”(当时希什的那本书还没有出版,虽然被汇总在该书中的所有研究都已完成了),虽然这个消息的性质有点含糊不清(“好像已经解决了”),但是立刻引起了极大的兴趣(不过还有点不相信)。与这个报道有关的还有一些关于这个题材的最新消息。例如,美国最有权威的拓扑学之一H · 惠特尼和重要的“组合”学派的领导人W · T · 塔特(《肯普链和四色问题》《实用数学杂志》1972年第2卷)一起执笔详细论述了肯普的思想(肯普的思想还和“用机器”来解决四色问题有联系!),又如在拥有广大读者的《美国数学月刊》(1972年第79卷)上发表了杰出的应用数学专家T · L · 萨蒂的重要文章(《对格思里四色猜想的十三种有趣变化》)。但是那时报道还没有得到证实,因为即使使用电子计算机来解决这个问题,也需要进行大量的工作。
之所以没得到证实,是因为为时过早,而不是不可靠!美国近几年来,详细研究肯普思想的是一大批精通程序设计的数学家——图论和组合分析专家(例如希什)以及熟悉组合分析的程序设计家(例如J · 科克);程序设计家是负责合理地使用电子计算机来进行组合计算和逐一检查各种方案的。这种大量的劳动结果应当获得成功——事实也正是这样。
1976年9月在《美国数学会通报》(第82卷第3期)上出现了K · 阿佩尔和W · 黑肯写的一篇简讯(包括较详细的引文,其中一部分是还没有发表的文字),报告四色问题已经解决了。
我国早在阿佩尔和黑肯的简讯刊登之前就首次报道了这一值得注意的事件,这个消息是从纽约大学“计算机科学系”主任J · 施瓦茨那里得到的(在美国许多大学里都有计算机科学系,相当于我国的“应用数学系”)。施瓦茨率领了一个美国代表团参加1976年9月在莫斯科举行的有关“机器数学”问题的国际会议,他在苏联逗留期间和他的许多同事谈了这个轰动一时的新闻。当时施瓦茨着重指出,美国数学家的这件工作的正确性是毋庸置疑的,因为有一个很大的专家班子把这件工作的每一步都仔细地检验过了。
阿佩尔和黑肯的简讯指出,最后结果要求分析清楚相当繁杂的组合结构,这种结构包含二千多个具体的图形,所以不用电子计算机而要完成这项工作是完全不可思议的。作者们还希望,只要更仔细地分析所有的可能性,就大约可以减少结构数目百分之二十五,这样就可以稍微减少一些解决四色问题所需的机器时间量,但是没有任何理由指望可以用“手工”(不用电子计算机)来证明四色假设。
因此,今天可以认为四色问题已经解决了:正像默比乌斯早就猜想的那样,四种颜色事实上是足够了。
四色问题的解决是个重大的科学事件,这不仅是(甚至主要不是)由于又猜中了一个恼人的科学之谜,也不仅是我们现在坚信任何平面图都可以用四种颜色来正确地着色——这个事实本身既没有理论价值,也没有实用价值。重要的是这样一种情况,即用早就成功地用于研究技术问题、宇宙问题或物理问题的方法——科学家与计算器(人和电子计算机)密切合作的方法来解决纯理论的着色问题的。可以期望,这种“混合的”研究班子能胜任许多最著名的数学家至今都对之束手无策的任务。
(刘定一译)
————————
① 显然,可以用所谓球极平面投影将球面上的每张地图变为“拓扑等价的”平面地图,球极平面投影就是球面从“北极”到“南极”的切面的中心投影。因此四色问题在平面和球面的情况下,数学上是等价的。
② 可用图形表示如下: