那些突如其来地发生急剧变化的事件一向不接受数学的分析。现在有一种来自拓扑学的数学方法以七种“基本突变”为例描述了这类现象
[提要]“突变理论”(Catastrophe Theoay)是最近十年来国外数学界提出的一种新的数学理论。它运用拓扑学、奇点理论和结构稳定性等数学工具,研究自然界各种形态、结构的不连续的突然变化。Catastrophe原意是指灾难性的突然变化,以强调变化过程的间断性,有时也直接表示市场的崩溃、战争的爆发、地震的发生等带来灾难性后果的变化。
这个理论由法国数学家伦尼 · 汤姆(René Thom)最早提出,1972年他出版了《结构稳定性和形态发生学》一书,系统阐述了这个理论,逐渐引起了广泛的注意。国外学术界大多给以肯定的评价,有的甚至誉为“数学界的一次智力革命——微积分以后最重要的发现”,本文作者齐曼(E. C. Zeeman)就是一个积极的支持者。但也有强烈的反对意见,甚至认为这种理论完全是欺世盗名的。
齐曼是英国瓦维克(Warwick)大学著名的数学教授。1970年以前研究拓扑学,以后把注意力逐渐集中到突变理论,特别是对于这个理论模型的运用,他做了很多工作。《突变理论》(原载《科学美国人》,第234卷,1976年4月号)一文比较集中地反映了他的看法和某些研究成果。
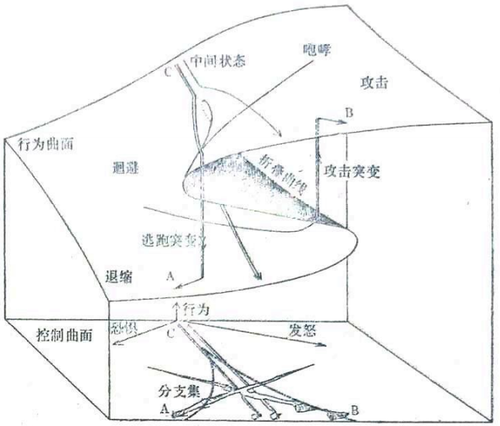
齐曼认为,微积分模型解释了光滑地连续变化现象,突变理论模型则描述了不连续的突然变化现象,如水结成冰或化成气、弹性梁受挤压而弯曲、胚胎的变化、人的情绪波动等等。突变理论用拓扑学的曲面折叠概念来描述这些突变现象。例如,在狗的进攻模型中,狗的突然进攻和突然逃跑是由发怒和恐惧这两个相互矛盾的因素所控制的。在齐曼的模型中,这两个因素作为两轴构成控制平面,用垂直于平面的轴作为行为轴。在通常的情况下,行为是发怒和恐惧程度的函数,是一个三维空间中的曲面。曲面中间部分的折叠把曲面分成顶、中、底三叶,分别表示攻击行为,中间状态和逃跑行为。因此,根据狗发怒和害怕的程度就可以画出尖顶的边界,说明狗的行为如何突然变化。
齐曼介绍了突变理论在物理学、工程学、医学等方面的应用。如在范 · 德 · 瓦尔(Vander Waals)方程中温度和压力是两个相反的因素,密度在行为轴上标出,顶叶是液态,底叶是气态,两个突变表示沸腾和凝结,尖顶的顶点是临界点,尖顶区里液态和气态同时存在。这种模型可以对物理学上定律加深理解。此外,齐曼还介绍了这个理论在社会科学方面的应用,如预测战争对策、市场变化、解释心理学现象等。这方面的问题还需另作分析研究(文章中这方面的内容未译出)。
汤姆对所有这些突变都进行了分类,他证明如控制因子不多于四个,突变模型可归结为七种基本突变。目前,突变理论模型正广泛应用于物理学、工程技术、生理学、医学等方面,特别是用到基因密码的翻译和语言、文字同思想的关系等问题上,引起很大的兴趣。突变理论究竟如何,要看未来十年的实验检验。
科学家常常用构造数学模型的方法来描述事件。事实上,如果这样的一个模型特别成功,那就可以说不但描述了事件,而且也“解释”了事件;假使这个模型能够归结为一个简单的方程,甚至可以把它叫做一条自然定律。三百年前,牛顿和莱布尼茨在构造这类模型时发现了著名的微分法。牛顿本人在表达他的引力定律和运动定律时用了微分方程。麦克斯韦(James Clerk Maxwell)则把微分方程用于它的电磁理论。爱因斯坦的广义相对论最终归结为一组微分方程。这类比较不那么著名的例子还可以举出许许多多。然而,微分方程作为一种记叙性的语言也有其固有的限制:它们只能描述那些连续变化和光滑变化的现象。用数学的语言来说就是:这些微分方程的解必须是可以微分的函数。但这类有规律、有很好性态的现象,相对来说是很少的。相反,世界上充满了突然变化和不可预测的事件,这些都要求不可微分的函数。
有一种关于不连续的、发散现象的数学方法,到最近才发展起来。这个方法有可能描述自然界各种形式的进化,因而它体现了一种更有普遍性的理论;它能特别有效地应用于由逐渐变化的力量或运动而导致突然发生变化的情形。由于这个原因,这一方法被称之为突变理论。物理学中有许多事件,现在都可以看作是数学突变的事例。但这个理论最重要的应用,毕竟还是在生物学和社会科学方面,那里不连续的、发散的情况几乎无所不在,而其它数学方法至今证明无效。突变理论能对到今天还是“不精密”的科学提供一种数学语言。
突变理论是法国Bures-sur-Yvette高级科学研究院的汤姆创立的。他在1972年出版的《结构稳定性和形态发生学》一书中介绍了他的思想。这理论导源于拓扑学,它是涉及多维空间曲面性质的数学分支。同拓扑学有关,是因为自然界的基本力量可以用关于平衡的光滑曲面加以描述,当这一平衡被打破时,突变就发生了。因此,突变理论的问题是要描述各种可能的平衡曲面的样式。汤姆用很少几种最原始的形式,即他称之为基本突变的,把这个问题解决了。对于不超过四个因子控制的过程,汤姆证明正好有七种基本突变。汤姆定理的证明很难,但证明的结果却比较易于了解。这些基本突变本身,不必看证明就可以懂,并可以用到科学问题上。
进攻模型
突变理论的模型的性质,最好用例子来说明,我们从研究狗的进攻模型开始。洛仑兹(Konrad Z. Lorenz)曾指出,进攻行动受两个互相矛盾的倾向所制约:发怒和恐惧。他还指出,对于狗来说,这两种因素在某种程度上可以测量出来。一只狗的发怒和张嘴、露齿程度有关,其恐惧程度则可从它的耳朵向后拉平多少反映出来。使用面部表情作为狗的情绪状态的指标,我们可望弄清狗的行为的变化是如何因情绪变化而变化的。
在两个互相矛盾的因素中如果只有一个因素出现,狗的反应比较容易预测。如果狗发怒而不害怕,某种进攻行动比如发动攻击是可以料到的。当狗受了惊吓而未发怒,进攻行动就未必发生,狗多半会逃走。如果没有刺激,预测也很简单:狗将处于某种中间状态,同进攻和驯顺都不相干。
如果狗同时又发怒又恐惧该怎么样呢?这两个控制因子是直接冲突的。有一种和不连续变化不相适应的模型预测,两种刺激将相互抵消后回到中间状态。这正好暴露了这种简单化模型的短处,因为实际上中间状态最少可能发生。当一只狗又发怒又受惊,采取两种极端行为的概率都很高:可能攻击也可能逃走,但不可能保持无动于衷。从突变理论中导出的模型的长处在于能估计出取二个值的概率分布。另外,这个模型还提供了一个预测在特殊情况下狗将选择什么行动的基础。
构造模型,首先要在水平面上划两个轴,表示发怒和恐惧这两个控制参量,这个水平面称为控制面。度量狗的行为的第三轴垂直于前两轴称为行为轴。我们可以假定狗的各种可能行为方式都平滑而连续地排列着,如开始是仓皇逃走,继而退缩、回避、漠然、惊叫、直到咆哮进攻。最有进攻性的行为假定在行为轴上取最大值,最少进攻性的则取最小值。对控制面上的每一点(即对发怒和恐惧的每一种组合),至少存在一种最可能的行为。我们就直接在控制面的那一点之上标出空间上一点,使之最大限度地表示出上述行为。对控制面上许多点来说,不论是恐惧还是发怒占优势,只有一个行为点与之相应。但接近于图形中心部分,发怒和恐惧的程度差不多相等,控制面上的每一点都有两个行为点:一个在行为轴上有较大数值,表示攻击行为;另一个有较小数值,表示驯顺行为。此外,我们还可以注意到两点之间有第三点,表示最小可能的中间行为。
如果对整个控制面上每一点都画出行为点,并能连成一片,则形成一个光滑曲面:行为曲面。这曲面有一种整体性倾斜,从发怒占优势的高数值区域到恐惧占优势的低数值区域。但这种倾斜还不是它最主要的特征。突变理论表明,曲面中间一定还有一个光滑的打了褶但没有皱的二重折叠,造成从曲面前部到后部的夹缝,最后出现折叠中三叶会合的奇点(见图1说明)。正是这一折叠才给予这个模型最有趣的特征。行为曲面上的所有的点表示狗的最可能行为,有一个例外是中间叶,它表示最小可能的行为。通过突变理论,我们可以根据某些控制点上的双重行为得出整个行为曲面的形状。
图1狗的进攻可用一种基本突变理论模型描述。这个模型假定进攻行为受控于两个互相冲突的因子,发怒和恐惧,标为水平面,即控制面上的两根轴。狗的行为从攻击到逃跑表示于垂直轴。对发怒和恐惧任何一种组合,从而对控制面上的任何一点,至少有一种相当的行为形式,用控制面相应点上方行为轴的适当高度上的一个点指示出来。所有这些点的集合构成行为曲面。在大多数情况下,只有一种可能的行为方式,但发怒和恐惧的程度如果大致相等,就会有两种方式:一只狗既发怒又害怕,就可能或者进攻或者逃跑。因此在图中央有两叶表示最可能的行为,两叶用第三叶连接起来形成一个连续的折叠面。这第三叶或中间叶(阴影部分)同另外两叶意义不同,表示这种中间状态的最小可能的行为。行为曲面的折叠朝原点方向越来越狭,直到最后消失。确定折叠边缘的线叫做折叠曲线,它在控制面上的投影是一条尖形曲线。由于这个尖顶标志着行为出现双枝的区域的边界,因而叫做分支集,这个模型叫做尖顶突变。如果使一只发怒的狗害怕起来,它的情绪沿控制面上的轨道A变化。行为曲面上相应的路径在顶叶上向左移动直到达到折叠曲线为止;然后顶叶消失了,行为点的路径一定突然跳到底叶。这时狗放弃攻击而突然逃走。同样,一只受到惊吓的狗被激怒以后,沿轨道B移动。狗保持在底叶,直到底叶消失为止,然后跳到顶叶,狗不再畏缩而突然发动攻击。狗如果同时受到激怒和惊吓,必然沿着C上的两条轨道之一移动。究竟移动到顶叶变为进攻还是移动到底叶变为驯顺,则严格取决于发怒和恐惧的数值。这时一个很小的刺激会产生一个很大的行为变化:这现象就是发散。
为了了解怎样用模型预测行为,我们必须研究狗对改变刺激的反应。假设狗的初始情绪状态是中间的,可以用控制面上的原点表示。这时在行为曲面上标出的狗的行为也是中间的。如果某些刺激增强了狗的怒气而不使之害怕,那么在行为曲面上标出一个光滑地向上改变的行为方向,趋向于进攻的态势,当发怒增强到足够程度,狗便会攻击。如果狗的恐惧开始增强,而发怒气仍保持高水平,那么控制面上表示这些情态的点一定向中央部分伸展过去。而表示行为的点也当然跟着移动。但因为行为曲面在这一区域不很陡,行为变化很轻微,所以狗仍保持着进攻态势。
当恐惧继续增强,最后行为点必然达到折叠的边缘。模型显然给人以新的启发。在折叠边缘上,顶叶经过向下折叠以后,其效果已经消失。这里只要稍微增加一点恐惧,顶叶就不起作用了。因此,行为态势将直接取决于图的底叶,它表示完全不同的行为方式。顶叶的进攻态势再也不可能了,不可避免地突然、实际上是突变式地变为驯顺态度。于是,这一模型预测到,如果一只狂怒的狗逐渐恐惧起来,最后将中止进攻而逃走。这种行为的突然变化可以叫做逃跑突变。
此图也可以预测存在一个相反的行为模式:攻击突变。当狗处于恐惧占优势的初始状态时,其行为稳定在底叶,但随着怒气的充分增大,穿过折叠的对边跳到顶叶,处于攻击态势。换句话说,一只逃跑的狗,如果置于怒气渐渐增大的状态下,可能突然攻击。
最后,一只狗最初处于中间状态,后来怒气和恐惧同时增大,其行为将怎样呢?行为点开始在原点上,在两种对立的刺激影响下,在图上笔直地向前移动。到达奇点时,行为曲面发生折叠,行为点或者在狗更多进攻性时向上面一叶移动,或者在狗更少进攻性时向下面一叶移动。究竟到哪一叶,严格取决于狗在到达奇点以前的态势。此图被称为发散的:初始条件的一点很小变化都会引起最后状态的重大变化。
尖顶突变
在行为曲面上,标志着经顶叶折向底叶边缘上的那条线,称为折叠曲线。它投射在控制面上,形成了一条尖形的平面曲线。由于这个原因,这个模型叫做尖顶突变。这是七个基本模型中最简单的一个,也是至今最有用的一个。
控制面上的这条尖形曲线,称为尖顶突变的分支集合,规定了突然变化可能发生的范围。当系统的状态在这一集合之外,行为的改变量作为控制参量的函数平滑而连续地变化着。甚至进入尖形曲线内部,一时也看不到急剧的变化。然而,当控制点从头至尾穿越尖顶时,突变就不可避免了。
分支集合内的每一点都有两种行为方式,外面只有一种。而且,即使行为曲面有三叶,尖顶中也只有两种行为方式。因为我们曾用折叠部分的中间叶表示最小可能的行为。中间叶的存在使行为曲面保持平滑和连续,然而行为点并不布满整个中间叶,事实上控制面上没有一条渠道能使行为点进入中间叶。一旦跨过折叠曲线,行为点就要在顶叶和底叶之间跳跃,因此,中间叶是难以接近的。
构造这一模型,是从一个本质上是决定性的假设出发的:狗的行为能够从反映在面部表情上的情绪状态预测到。最后,用图表示的模型乍看上去似乎违背了这个假设,因为对于给定的情绪状态有两种可能的行为方式,就不可能作出毫无含糊的预测。事实上如果我们仅仅知道当前的情绪状态(假定这一状态在图的双值区域以内),我们当然不能预测到狗将干什么。不过当我们附加某些条件时,就可以提高这个模型的决定作用,也可以使它更复杂些。倘若我们对狗现在和前一段的情绪状态都知道,狗的行为就可以预测。
进攻性当然不只是狗的特征,这个模型也描述了一种可以同样运用于其它物种的机制。例如,考虑某些热带鱼有一种在珊瑚礁建立永久巢穴作为领土的行为。在这种情形中,控制进攻因子可以是来犯鱼的大小和接近窝的程度。鱼的攻击行为将再次被描述为一种尖顶突变。一条鱼远离巢穴寻找饲料,碰到大鱼时将会逃跑;但一旦逃到自己领土的“防御”边界,突然改变态度,转过来保卫自己的巢穴。反过来,如果鱼在它的巢穴里遇到危险,它将驱逐来犯者,但一到达自己领土的“攻击”边界,就会放弃追赶而返回巢穴。从巢穴到改变行为地点的距离,将取决于尖形曲线的分支集合。由于尖顶模型的样式,这个模型可以令人感兴趣地预测到“防御”范围比“攻击”范围要小些。此外,这两个边界的大小取决于敌我力量的对比。一条来犯的大鱼更靠近巢穴才会激起这条鱼起来战斗。这个模型还很容易说明鱼的行为的一种可见特点:这种有领土的鱼配对时,对于偶尔接近巢穴的对象会进行更有力的抵抗。
动力的作用
还留下一个重要的问题来:什么是动力?在进攻模型中是什么迫使狗表现出最可能的行为?在自怜模型中为什么最可能怀有的心情正是所采取的那一种?
像突变机这样一个物理系统中的能量极小值,是所谓吸引子概念的一个特例。这里它是最简单的一种吸引子,一种单一的稳定状态,其作用好像一块磁石的吸引子:在它影响范围内的什么东西都要被它拉过去。在吸引子的作用下,系统呈现出静态平衡。
心理学模型中一定也有吸引子,虽然不一定这么简单。一个动态平衡系统的吸引子,是由系统经历各态的全部稳定循环所构成。例如,正在用弓拉的提琴弦一再按其共鸣频率重复同样的位置循环,这些位置循环就代表弦的吸引子。
在心理学模型中寻找吸引子,显然要到大脑的神经机构中去找。大脑当然比提琴弦复杂得多,了解得却很少,但也知道亿万神经原组成大规模互相连结的网络,形成一个动力系统。任何一个动力系统的平衡态都可以用吸引子表示出来。有些吸引子可以是单一状态,但大多处于稳定状态的循环或者更高级的类稳定循环之中。头脑的各部分是互相影响的,因而吸引子的出现与消失有时很快,有时很慢。当一个吸引子让位于另一个吸引子,系统也可能保持稳定性,不过情况常常不是这样,大脑状态会出现突变性的跳跃。
汤姆的理论讲,在最简单的吸引子——静态平衡点之间——所有可能的突然跳跃都是由基本突变决定的。因此,倘使大脑动力只有点吸引子,它就只能表现为基本突变。但实际上并不是这样,还有更复杂的吸引子,明显的证据是:大脑的X节律波是一个循环吸引子。支配循环吸引子和高维吸引子之间跳跃的法则,现在还不知道,它们必然不仅包括基本突变,还包括一般化的突变,对这些问题的研究是今天数学研究的活跃领域。因此还没有描述整个大脑动力系统的完备理论。然而,基本突变仍然对某些大脑活动提供了有意义的模型。模型是清楚的,有时也使人感到简单,但是它们所依据的主要数学理论隐含地以神经网络的复杂性作为基础。
大脑动力的吸引子概念,提供了我们的人类行为和动物行为模型中所需要的东西。
担负像自怜这类情绪的神经机制是不知道的,但存在着一种稳定状态的情绪,就意味着这个机制是一个吸引子。事实上,在自怜模型中行为曲面的每一点都相当于一个支配着情绪的大脑中那个系统的吸引子。如果神经系统受到什么干扰,它立即在吸引子的影响下回到行为曲面上来,正如突变机制恢复到平衡一样。当一个吸引子的稳定性被打破,让决定情绪的系统接受另一个吸引子的影响,并朝着它迅速移动的时候,情绪的急剧变化就出现了。
尖顶突变的特征
前面的例子和分析提示了尖顶突变的某些共同特征。一个不变的特征是:行为都在区域上方,部分是双重的,并可以观察到从一种行为方式到另一种方式的突然变化。此外,突然变化的模式还呈现一种滞后效应,就是说,从顶叶到底叶的变换并不发生在从底叶到顶叶变换的同一点上。尖顶中央并不发生变化,一直推迟到到达分支集合为止。另一个特点是:在尖顶里面行为是双重的,行为轴的中间地段很难接近。最后,模型意味着有可能发散,使系统初态的小扰动最后会变成终态的大差别。这五种性质:双态性、突然变化、滞后、不可接近性和发散性,由于模型本身而彼此有关。如果有一个在过程中显露出来,也应当找到其它四个,如果不止找到一个,就应当考虑选择尖顶突变来描述这个过程。
对于许多物理学(一种运用高度发展的数学语言的科学)上的问题,突变理论也有助于理解。一个例子是物质在液相和气相之间的转化。我们可以作为尖顶突变而重写范 · 德 · 瓦尔方程,以温度和压力为两个相反的控制因子,密度为行为轴。顶叶是液相,底叶表示是气相,两种突变表示沸腾和凝聚。尖顶的顶点是临界点,同时存在液相和气相。绕过尖顶背后,液体可以不经沸腾而变成气体。
物理学中的另一个尖顶突变,来源于18世纪欧拉(Euler)的工作,即弹性梁在水平挤压和垂直荷载下的弯曲。挤压是破裂因子,荷载是正常因子。加强挤压,使图形上的行为点进入尖顶区域,在这里,梁有两个稳定状态,一个向上弯曲,一个向下弯曲。如果梁最初是向上弯曲的,荷载增加时,行为点的移动会跨过尖顶区,使梁突然向下弯曲。这种情况如果是发生在一座桥的支持桁架上,就既是数学上的突变,也是现实中的突变。
物理学中另一个绝妙的例子,是由于光线在弯曲表面上的反射和折射形成的明亮的几何图案,即所谓光焦散。一种熟悉的焦散是尖顶形曲线,一杯咖啡的表面由于阳光的照耀有时会出现这种焦散,它是由太阳光线从杯子内部的反射而造成的。
另一个熟悉的焦散展现了短暂的和立体的亮度的不连续性,即在太阳光下游泳池底部变化着的图案。雨后的虹是一族颜色的散射。一道光线照射到凹面镜上或者通过球面镜或柱面镜(例如一只泡泡或者注满了水的烧杯),会产生许多复杂的焦散现象。在这里应用突变理论后,加深了对现象的理解。汤姆曾指出:稳定的焦散只有3种类型的奇点。对光焦散现象进行突变理论分析的数学精巧性在于,这里没有用动力学,用的是对极大极小给以同等重要地位的变分学。
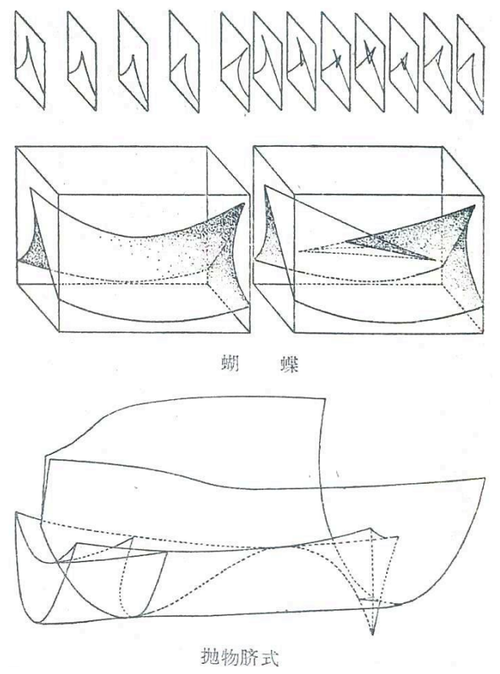
图2对剩下的两种突变只可用截口加以解释,因为即使其分支集也超过了三维。蝴蝶突变的四维分支集用三维截口表示。第四维是蝴蝶因子,如果碰巧它表示时间,那么一个截口的结构就能引申出他截口来。图形中从左到右的移动反映倾斜因子的变化。二维“薄片”可以更清楚地显示这些因子的作用。抛物脐形突变的四维分支集合也用三维截口表示。这是照英国兰开斯特工艺学校的高德温(Godwin)事先用计算机准备的图形画的。
尖顶突变是三级图像:二个控制参量需要二维,行为轴还要一维,其实行为轴不一定只表示单独的行为变量,例如在脑功能模型中,它可以表示亿万神经原同时变化的状态。然而突变理论指出,总是可能选出一个单独的行为变量,画出仅仅相对于行为轴的行为曲面,从而得出我们熟悉的三维图像。
如果把图像减为二维,结果会产生一个更加简单的模型:折叠突变。折叠突变中只有一个控制参量,控制空间是一条直线,分支集是线上的一个单独点。行为空间是一条抛物线,一半表示稳定状态,另一半表示不稳定状态。这两个部分由一个直接在分支点之上的折叠点所分开。
分类定理
折叠突变可以看成是尖顶突变折叠曲线的截口。尖顶突变也可以当作许多原点上只有一个新奇点的折叠突变的堆砌。更复杂的高维突变可以按同样办法构成:由每一个都在原点上有一个新奇点的许多低维突变所组成。
如果控制空间是三维的,行为空间仍然是一维的,唯一的一个四维突变就可以构造出来。行为曲面变成一个三维超曲面,沿整个曲面的折叠代替沿曲线的折叠,这样的图形很不容易画得让人看出来。分支集合不再是二维平面上有奇点的曲线,而是在边缘上遇到尖顶的三维空间的曲面。一个新的奇异性发生在原点上,叫做燕尾突变。因为是四维图像,整个燕尾突变是画不出来的。我们只能画出它的三维分支集合,由此可能得到关于燕尾的某种几何直觉,正如通过画出尖顶的二维分支集合,并记住行为曲面在尖顶以内是双重的就能够描述尖顶突变,这种突变叫做燕尾,因为它的分支集合看上去有点像一只燕尾。这个名字是一位法国盲人数学家贝纳德 · 毛林(Benard Morin)建议的。
如果再加上另一个控制参量,产生一个五维突变。折叠,尖顶和燕尾又作为截口出现,而一个新的奇异性由于几个曲面的交截形成一个“口袋”。“口袋”的形状和它的截口,叫做蝴蝶突变。它的分支集合是四维的,因而画不出来,只能通过二维或三维的截口来说明(见图3)。
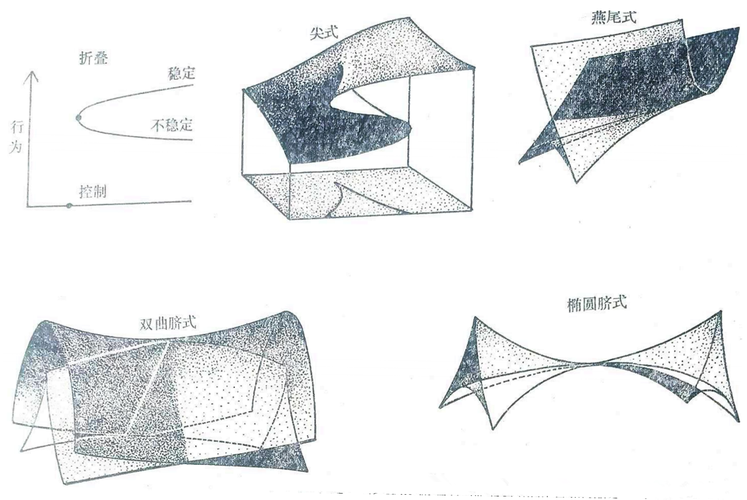
图3五种基本突变图提示了它们的几何本质。折叠突变是尖顶突变的折叠曲线的一个截口,其分支集合由一个单独的点所组成。尖顶是可以全部画出来的最高维数的突变。燕尾是四维突变,抛物脐状突变和椭圆脐状突变是五维的,这些图只能画出三维分支集,表示不出行为曲面。
当控制空间是三维、行为空间是二维时,形成两个以上的五维突变。这叫做双曲脐形和椭圆脐形突变。像燕尾式,有两个带尖形边缘的曲面组成分支集合,它们是三维的,可以画出来。最后,由一个四维控制空间和一个二维行为空间所产生的六维突变,叫做抛物脐型。它的几何形状是复杂的,也只能画出它的分支集合的截口。
增加控制空间和行为空间的维数,可以构造出无限的突变序列。俄国数学家阿诺尔德(V. I. Arnold)已经至少对25维进行了分类。但在现实世界的现象模型中,是上面所描述的七种可能最为重要,因为它们具有不超过四维的控制空间。由空间位置和时间所决定的各种过程的特殊同类性,不能多于四维的控制空间,因为我们的世界只有空间三维和时间一维。
即使画不出的突变也可以用模型现象加以解释,它们的几何形状完全是确定的,虽然不能从图上看出来,但点在行为曲面上的运动可以进行解析地研究。每一突变都用势函数来定义,而且在每种情况下行为曲面都是由势函数的一阶导数为零的点所构成的图形。
汤姆理论的力量在于它的一般性与完备性。它指出,一个过程如果由某一函数的极大值或极小值所决定,而且由不超过四个因子所控制,则行为曲面的任何奇异性一定类似于上面指出的七种突变之一。如果一个过程仅仅由两个控制因子决定,则行为曲面只能有折叠和尖顶。这个原理本质上说明,在任何包含两个原因的过程中,尖顶突变是可能发生在图上的最复杂的事。这个原理的证明在这里介绍就太专门、太长了,但它的结论却十分简要:只要连续变化的力量有突然改变的效应,这个过程一定可以描述为一种突变。
七种基本突变描述了控制因子不多于四个的所有可能的不连续现象。每一种突变都同一个势函数相联系,其控制参量用系数(a,b,c,d)表示,系统的行为决定于变量(x,y)。每一个突变模型中的行为曲面是由势函数一阶导数为零的一切点所组成的图像,当有两个一阶导函数时,二者都等于零。
神经性厌食症
蝴蝶型突变的第二个应用,也是最丰富的应用,是有关神经性厌食症的。这种主要在青春期少女和青年妇女中产生的神经紊乱,使得她们的饮食状况恶化到不吃东西。其模型由我和海维西(Hevesi)合作完成。海维西是英国心理医疗学家,曾用催眠疗法治疗厌食症。不久以前他调查了1000名厌食症病人,其中只有一个人说曾被完全治愈过。
在厌食症的初期,不吃东西导致饥饿,有时甚至死亡。随着时间的推移,病人的态度会倾向于吃食物,但其行为更加反常。通常大约两年以后发展到第二期,称为贪食期,这时患者交替地绝食和贪食。这种双重行为明显地可看作是一种突变,在厌食症患者的后一时期,其行为可在两个极端之间突然跳动,而拒绝采取介于二者之间的正常行为。突变理论提出一种理论上的治疗建议:如果能按照蝴蝶突变引进一种“分叉”,那么恢复正常的途径是可以得到的。
这一模型的行为曲面用来表示病人的行为,其次序是从不可控制的滥吃到吃得过饱最后到绝食不吃。这当然提供了大脑基本状态的某些指标。但正如在进攻模型中那样,我们关心的那种情绪状态,可能最初产生于周围神经系统。心理学上的论据表明,行为变量应是一种量度,表示周围神经系统从身体各部分来的信号输入量和从大脑皮层方面来的相反的信号输入量之间的相对量值。对正常人来说两种输入量在某种意义上是平衡的,而在厌食症患者,其中一个或另一个占着优势。
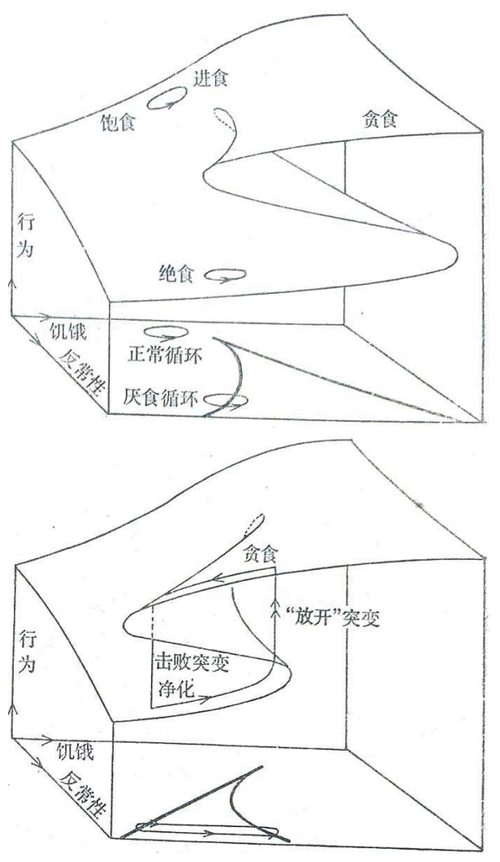
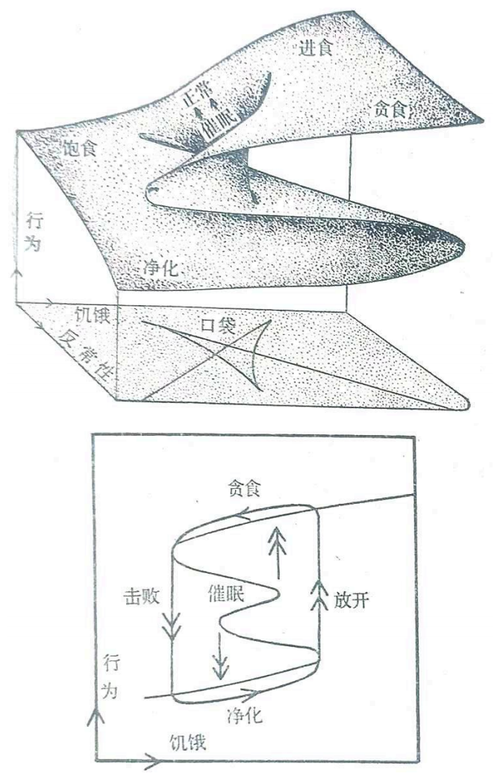
图4神经性厌食症,一种青春期少女和青年妇女患的由于神经紊乱而不吃东西的病症,可以用蝴蝶型突变描述。控制参量是饥饿和对食物的反常态度。对正常人来说,饥饿导致一个想吃东西和吃饱之间的循环。对厌食症患者,由于变态心理,同样的饥饿导致完全不同的行为。在病的初期(上图),圆圈在行为曲面的下叶,患者保持平常的绝食状态。在第二时期(下图)诱发了自我控制这个第三因子的变化。当病人经过二年或更多时间失去自我控制以后,分支集合逐渐弯向左边直到饥饿圈通过尖顶的右半边。然后患者进入了后期循环:她绝食,直至饥饿使她发生“放开”突变,然后贪食,直至发生“击败”突变重又回到绝食,并且在她发觉弄脏了时把自己洗干净。
在控制参量中,饥饿是正常因子。正常人有节奏地在想吃和吃饱之间循环。破裂因子是厌食症患者对食物的反常程度。随着患者情况恶化,变态程度也逐渐增长。饮食更加艰难,一切种类的食物都不想吃。对糖类最初是回避,后来竟感到恐惧。
蝴蝶型突变的倾斜因子是失去自我控制,它能用周围神经系统减少相对量值来衡量。在紊乱的初期,患者的态度已经失常,但还能控制自己。这时她的情况处在曲面的底叶,其周围神经系统始终保持和绝食相适应的状态,即使当她正在吃最低限度食物的时候也是这样。
随着患者周围神经系统减少相对量值,她也失去控制,倾斜因子渐渐增加。结果尖顶摆向图形的左边(见图5)。如果移动得足够远,尖顶的右半边和厌食圈相交,病就突然进入第二期的发作,现在患者不再处于通常的第一期绝食循环,而被赶入后一个循环:从底叶跳到顶叶,又从顶叶跳回底叶。在典型的厌食症患者的语言中,当她说“放开”时,就发生从绝食到贪食的突变跳跃。人们毫无办法地注视“在她心中的怪物”狼吞虎咽地大吃几小时,有时还呕吐。当她筋疲力尽,感到厌恶、丢脸的时候,突变又回到绝食状态,许多厌食症患者把这叫做“击败”。
图5厌食症的处理,依赖于提出表示行为中间方式第三叶。蝴蝶型突变的第4个控制参量:使病人安心;它的增加可能构成新的行为。第4个参量的作用是在分支集合中设置一个口袋,以便产生行为曲面的中间叶。由英国心理医疗学家海维西发展起来的治疗体系,使病人安心的办法是鼓励病人进行催眠。最初病人进入或离开催眠状态,就是从中间叶到顶叶或底叶跳跃的突变,如上面下图所示。当治疗继续进行,病人的状态就从中间叶光滑地转移到口袋后面的正常行为方式。
后期由于“击败”而进入绝食的期间,和初期的通常的绝食是不同的。它位于行为轴的不同位置,把这种情况叫做“净化”也许更好些。早期绝食时,周围神经系统状态是大脑皮层的信号输入量占优势,不肯吃东西。在贪食期,周围神经系统是身体方面来的输入量占优势。基于“净化”时的状态又是大脑输入占优势,但这时又有身体方面输入的倾向以避免弄脏身体的成分在内。
从事催眠疗法的海维西设法使病人安心,减少她们的不稳定性,用催眠术使患者回复到接近正常的行为。厌食症患者的睡眠是不定时的。当她们醒来时,就体验由催眠者自然引起的催眠状态。催眠可表示周围神经系统的第三种状态,它位于贪食和净化之间的不可接近的地带。病人在绝食时以忧虑的眼光看整个外部世界,在贪食时又被外部世界所压倒,但处于催眠状态时她被孤立起来了。她的心情从需要食物和设法避开食物二者之间解脱出来,只在这时,才能使病人安下心来。
使病人安心的程度成为模型中的蝴蝶型因子,它在行为曲面中创造了新的一叶。它位于其它二叶之间,并最终将接近于尖顶后面正常区域的稳定状态。因为治疗通常从绝食状态开始,所以进入催眠是从底叶到中间叶的跳跃,解除催眠则是另一种突变,使病人的状态从中间叶跳到顶叶或底叶。
大约催眠两个星期,进行了7个催眠疗程之后,病人的变态心理通常会突然被打破,个人性情又和整体协调起来。当病人从催眠中醒来时,她会说这好像是“再生的时刻”,她能再次吃东西而不会过分了。看来催眠打开了大脑中的途径,使得周围神经系统获得更好的平衡,病人则重新接近正常行为。随后的催眠是为了进一步加强这种体验。
这里介绍的厌食症模型在许多方面是不完全的。我省略了另一个附加控制因子:昏睡。这因子支配了醒和睡二者之间的行为特征,也和进入熟睡及唤醒的突变相联系,因此在模型中从催眠到正常的途径由于省略了唤醒突变而使人感到困惑。这一模型的其它方面,我还没有讨论过。
厌食症突变模型的长处之一,是它解释了病人对自己的叙述。许多患者所描述的表面上不可理解的病情,用突变曲面的结构去看,就变得十分合乎逻辑。数学语言在这类应用中的好处,是心理学所不关心的。它能把本来当作不相关联的观察结果加以有条不紊地综合。
突变理论的未来
突变理论是一门年青的科学:1968年汤姆发表了他的第一篇论文。至今它已对数学本身引起极大反响。特别是为了证明它的一些定理,刺激了许多其它数学分支的发展。在这个理论发展中,最重要的突出问题,是关于普遍性突变的理解和分类以及在加入对称条件时所引起的更精细的突变。此外,还有许多问题涉及怎样才能结合其他数学方法、数学概念运用突变理论,如微分方程,反馈,噪声,统计和扩散理论。
这一理论的新的应用正在各个领域中进行探索。在物理学和工程技术方面,如波传播、曲面最小面积、非线性振动、散射和弹性理论所构造的各种模型已得到发展。Bristol大学的Michael V. Berry最近已利用脐型突变预测腐蚀和流体流动物理学的新结果,并用实验证实了这些结果。
在汤普逊(D'Arcy Wentworth Thomp-son)和威定(C. H. Wadding)的鼓舞下,汤姆的《结构稳定性和形态发生学》已广泛联系到胚胎学,但至今生物学家还很少在实验室里追随汤姆的思想。我已构成了心搏、神经冲动传播、胚胎中胚囊和索米茨(Somites)形成的突变模型。最近,库克(J. Cooke)在伦敦医学研究会实验室、爱耳斯塔耳(T. Elsdule)在爱丁堡医学研究会实验室所进行的实验,看来证实了我的某些预测。
如同本文叙述的模型所提示的,我自己的绝大部分工作还是人文科学方面。大量增加的研究者提出了许多根据突变理论得出的模型,未来十年内我期望看到这些模型为实验所证明。只有到那时,我们才能判断这个方法的真正价值。
汤姆用这个理论大力研究了语言是如何产生的。这是一个令人感到兴趣的思想:同一门数学不但能够为基因密码如何发展成胚胎,也能够为印刷字如何激发我们的想象提供基础。
(张奠宙译)