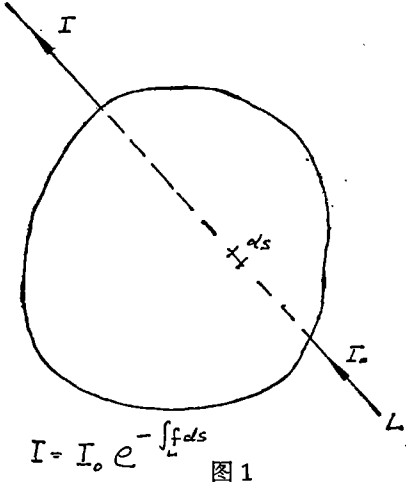
〔编者注〕1979年的诺贝尔医学生理奖,由子发展了计算机辅助X光层析法的功绩,授予Allan M. Cormack和Godfrey N. Hounsfield二人。Cormack在1963年与64年,发展了计算机辅助X光层析法的理论基础。Hounsfield在70年左右把计算机辅助X光层析法实际用于医学,使X光诊断有了飞跃的进展。这里先发表Cormack的得奖讲演。
1955年我在开普敦大学当物理学讲师时,Groote Sehuur医院的物理专家辞职了。南非法律要求有一个完全够格的物理学家来监督任何放射性同位素的使用,由于我是开普敦唯一的核物理学家,此要我每星期花一天半去医院照顾同位素的使用,1956年的上半年度我就担任了这一工作。我在放射科J. Muir Grieve博士下面工作,在我的工作过程中我观察到了放射治疗是如何安排计划的。一个女孩子把等剂量表叠加起来得出等剂量曲线,然后由医生审查和调整,这过程要一直重复下去直到取得一个满意的剂量分布为止。等剂量表是对于均质材料的,我想到人体是相当不均质的因此这些结果将受到不均质的影响而变样——这是物理学家当然完全意识到的事实。因此我想到为了改进治疗的设计就必须知道身体的衰减系数分布,并且这一分布必须在体外测定来求得。很快我就发现这一信息对诊断来说是有用的,将能构成一个或一系列的层面图,虽然我要到多年以后才学到“层面图”这个字眼。
那个时候已经知道YX线和伽马线的指数衰减,并将它用于平行放置的均质平板材料已六十多年。
这在1825年就已求得。1957年我在开普敦,在一个圆对称的样品上做了一个实验,样品由一个铝的圆柱外包一个木质圆环组成。结果如图2。这里画出了I(r)与r的关系,恒定的斜率说明木与铝质不变吸收率。即使这个简单的结果也有一些预报价值,可以看到靠近原点的三点所组成的线条其斜率与铝的其他点的斜率略有不同。后来向机械商店询问发现铝质圆柱内有一个塞子,其吸收系数比圆筒的其他部分略低一些。
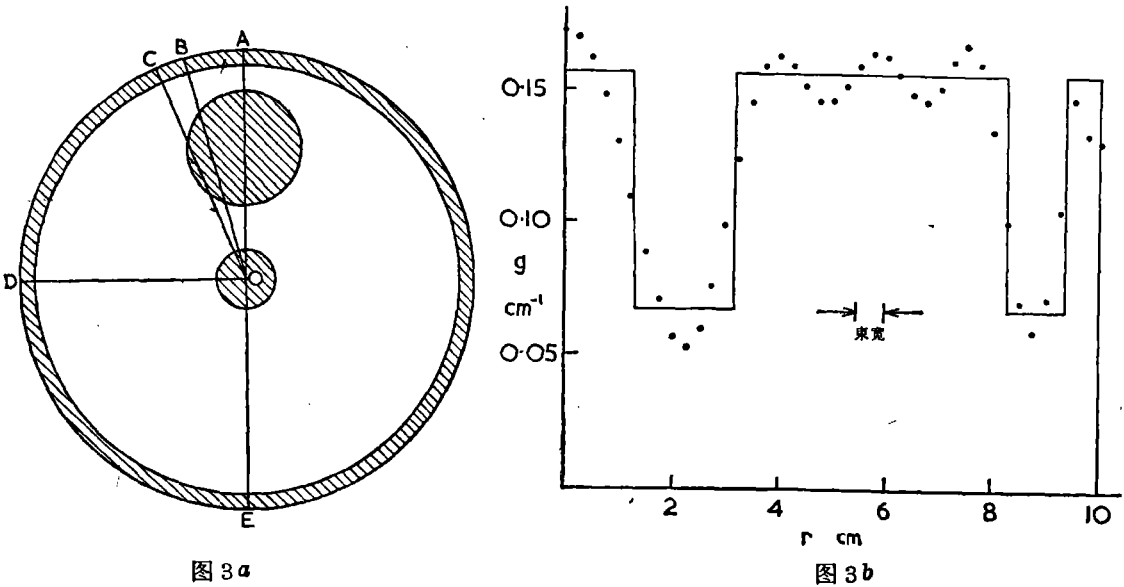
后来六年中断续地做了一些进一步的工作。利用f和g的傅立叶展开,我得到了与Abel的积分方程相像,但具有更复杂的核的方程式,得到了与方程式(1)相像,但具有更复杂的被积函数的结果。然而,它们也是从r到∞积分,这一关我还要再谈到。这些积分对于含有噪声的数据并不太好,于是研究出另一种展开,用它能够满意地处理带有噪声的数据。到1963年我已准备好用图2所示的装置在没有圆对称的人体模型上做实验。二根圆筒是二只准直管,里面装有放射源及检测器,允许5mn的钴60伽马线束通过人体模型,即它们之间的圆盘。在那个时候,我和学生David Hennage有来往,他想知道我是否有数字问题给他去解决,这样他就能够学习FORTRAN算法和如何使用计算机。由于他在处理一些主要误差来源带有统计特征的数据方面没有什么经验,看来由他帮助收集数据对他说来也是—个很好学习的机会。最后的数据是在1963年夏天的二天内收集起来的,进行了计算,结果如图3a及b。图3a是模型,这是一个相当混杂的物体。铝质外环代表颅骨,里面的有机玻璃代表软组织,二个铝盘代表肿瘤。铝和有机玻璃的吸收系数比大约为3,比异常和正常组织的吸收系数比大得多。选择了这样的吸收系数比的目的在于引起那些从事于使用正电子放射同位素进行现在称为发射扫描的工作者们的注意,当时这一工作尚在幼年时期。这一个数目大体是异常组织及肌肉内的放射性同位素浓度与正常组织内的放射性同位素浓度的比例。在对吸收作显而易见的校正以后,发射扫描的数学问题同透射扫描的数学问题当然是一样的。幻灯片的右面画出了衰减系数作为沿OA线距离的函数这一结果。沿着其他线作了同样的图表。实线是真值,虚线是计算值,一致性相当好。这些结果可以在显示屏上用灰阶来表示,但对于出版来说,想来用图表要好一些。
出版是在1963及1964年。当时实际上没有什么反应。对复本最感兴趣的请求是瑞士雪崩研究中心。如果能够把检测器或能源放到雪层下面的山里面去,这一方法对于山上积雪将会是有用的!
我的正常教学和研究工作使我非常繁忙,因此在七十年代初期以前我对这一课题想得很少。到了七十年代初期时,我才知道了Radon在线积分问题上的工作。大约在同一时候,我知道了这个问题已经在1936年在统计学上提出来,由这里Stockholm的数理统计研究室Cramér和Wold所解出。我也知道了Bracewell在射电天文学方面的工作,产生了与Cramér和Wold发现相同形式的解,也知道De Rosier及Klug(1968)在电子显微镜方面的工作,也知道了Rowley(1969)及Berry和Gibbs(1970)在光学方面的工作。最后,然而并不是最不重要的是,我第一次听到Hounsfield及EMI-扫描器,关于这些您们很快将要听到报告。从1972年开始,我对许多与CT*扫描或由此而生的许多问题发生了兴趣,我愿意告诉您们其中的某些内容。
前面我已经提到,我所求得的Radon问题的解是用从吸收系数所在的半径到样品外缘的积分来表示的。这意味着如果想要在一个环状区域内得到吸收系数,只需要得到与环内空穴不相交的线上的数据。这被称为空穴定理,是一个可以非常简单地予以证明的精确数学定理。然而,我已经指出过,把我的积分应用于含有噪音的实例时,来自外部观察的噪音在深入样品内部时被过分地放大,因此得到的这些积分在实际上是无用的。这一种由外向内的工作过程被称为“剥洋葱”,已经试了几种剥洋葱的算法。这些算法都有同样的特征,即深入样品内部时,外界数据的噪音也糟糕地传进去了。然而,据我所知,没有人产生过包含空穴定理在内的Radon问题封闭解,并由此可以证明外界噪音必须糟糕地传入内部。(Doyle和我发表了一个Radon问题的封闭解但发现这是错误的。很快就要发表一个撤销声明。)
包括空穴定理在内,噪音不传入内部的解对CT-扫描是极有价值的。第一,由于对没有兴趣的区域,即空穴区域不用X线,因此它将减少病人摄取的剂量。其次,它可以用来避免一些吸收系数显著变化的区域。这些显著的变化必然产生过火,使最后的图像模糊不清。以一个极端的例子来看,假如—个病人由于意外或某些医疗措施在体内有了一片金属。这将使含有这片金属的平面的CT扫描失真以至于无法辨识。可以用空穴定理来避免这片金属。在不那么极端的情况中,骨和软组织之间的界面上可以产生过火使软组织像失真。可以用空穴定理来避免骨和失真。
因此这里就有一个需要解答的问题,一个不利的答案不会使我们现在处境更坏一些,一个好的答案则将使图像有所改善。
在我1963年的论文中我已经,虽然并不是非常好感地指出,质子可代替X线用于扫描。1968年我的朋友和同事Andreas Koehler开始用质子制作了一些漂亮的放射线照相,他设想他这一工作可以清除一些我原来的关于用质子作层面图的疑问。
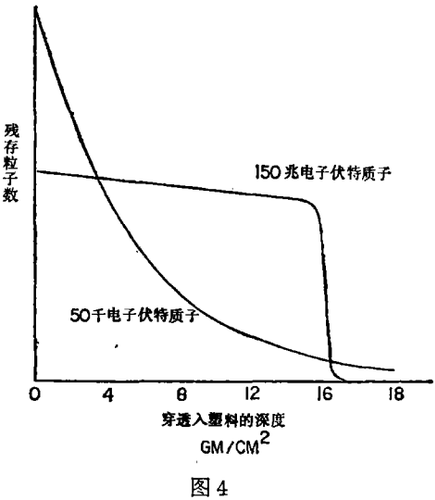
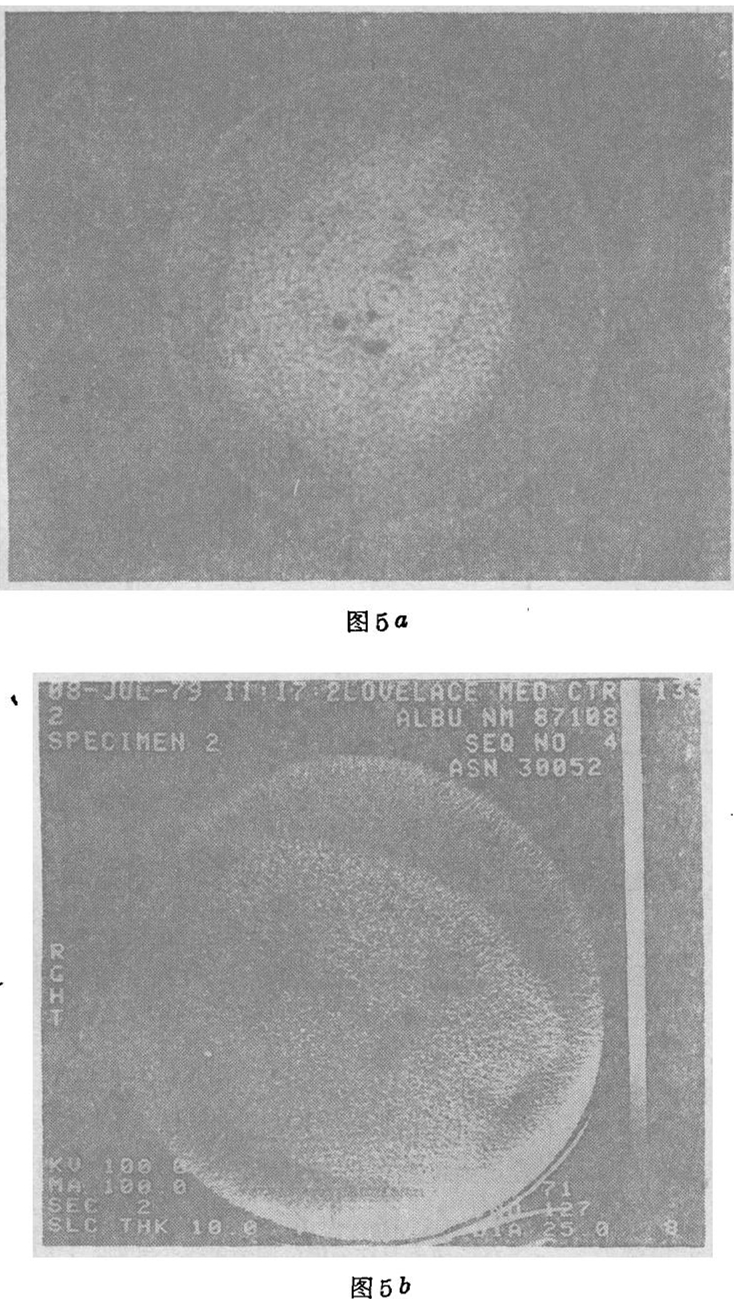
质子和X线的区别可由图4说明。X线的粒子数——距离曲线是熟悉的指数曲线。对于质子,先是核吸收引起的缓慢减少,继之的尖锐的下降。绝大部分质子透入材料一段距离,然后所有质子都在一个所谓质子射程的短距离内停止。就是这一个尖锐的下降使质子对它们路径上厚度或密度的变化非常敏感。在这个范围内比较二根曲线的斜率是对厚度或密度变化的灵敏度的一个粗略的测定。许多人也在想同样的事情,Crow等于1975年在Berkeley一个高能物理实验室使用相当大数量的设备,用α粒子制作了层面图。Koehler和我制作了一个简单的圆对称样品的层面图,目的在于证明二件事:(1)可以使用非常简单的设备和(2)我们能够用这台设备很容易地检测出0.5%的密度差。我们已经能够检测出有机玻璃样品上的机械应力或水分透入或透出有机玻璃所引起的0.1%或更少的密度差。最近,这一工作由Los Alamos的Hausen及Stewa-rd和他们的同事们所继续,我可以给你们看他们的—些结果。他们最近制作了人类器官的层面图。图5a是正常脑的X线扫描,使用一台Δ2020扫描器,剂量9拉德左右。Steward博士观察和进行了密度测量,发现死亡后四小时内白质丧失了水分和电解质因而灰质和白质的密度区别消失。图5b是同样样品的质子扫描,剂量0.6拉德,这张图大致地与X线扫描一样好。图5a及b分别示出固定在福尔马林(甲醛)中的心肌梗塞心脏的X线扫描(9拉德)和质子扫描(0.6拉德)图。根据Steward博士,在福尔马林(甲醛)内固定并不影响心脏组织的相对阻塞能力。这二张图像的质量也是大体相同的。取得数据的时间大致是一小时,但是LAMP加速器是脉冲的,只有6%的时间在工作。用连续的光束可在大约四分钟的时间内取得同样的数据——大致与原来的EMI扫描器相等的时间。我要感谢Hanson及Steward等把他们的资料提供给我。
为什么用质子?第一是剂量问题。Hanson及Steward的工作大约是0.6拉德与X线扫描所需要的9拉德相差很大。这点与理论上认为得到同样数量信息所需要的剂量,质子扫描比X线扫描要少五到十倍。这一计算值是符合的。第二/使质子静止下来的机制与X线被吸收或散射的机制不同,因此使用不同的辐射就应该看到不同的事情,特别是氢的分布。Koehler和我确实已经在二个场合下发现质子与X线扫描的对比反转,而这在理论上是预料到的。
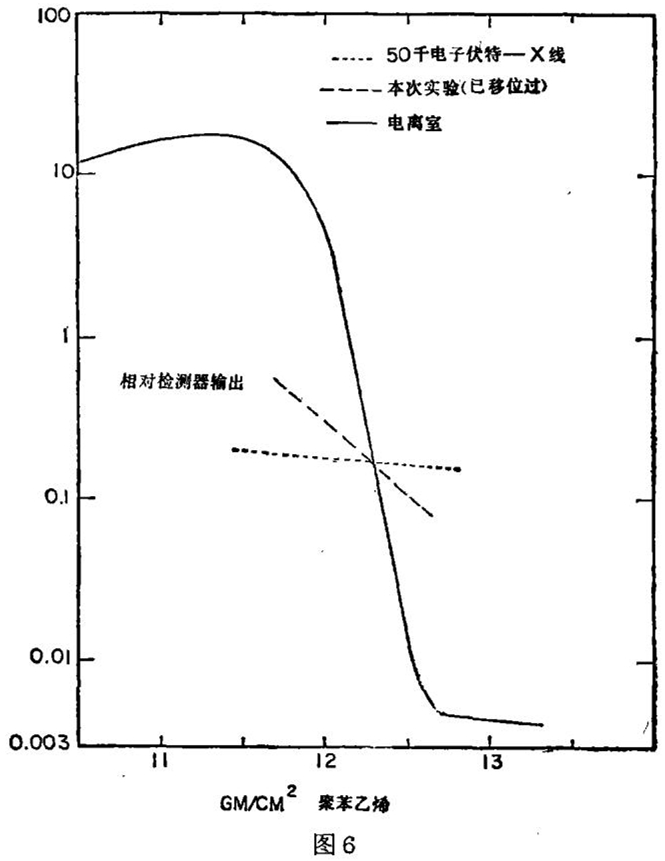
你们当然知道许多人是如何地对CT扫描器的高价大惊小怪的,因此你们可以想象如果建议把扫描器里的X线管改为更要昂贵得多的回旋加速器时,他们会说些什么!如果只从狭隘的诊断范畴去考虑,当然他们可能是对的。如果不去看我在比较X线和质子时给你们看的粒子数——距离曲线,让我们看一看电离——距离曲线,这是与治疗有关的。如图6所示。你们看到曲线在接近射程的终点时是在峰值(Bragg峰),然后极为尖锐地下跌,因此在射程的终点以外实质上已没有电离。R. R. Wilsno已经指出这二件事实对于治疗来说是重要的,也已经被Uppsala,Harvard及Berkeley在治疗许多不同病情时所证实。事实上,质子对某些病情的治疗要比X线优越得多。可以设想一个巨大的装有250兆电子伏特的质子加速器的中央区,配有许多,例如十个不同的出口,在这些出口上许多病人可以同时接受治疗。如果其中有一个出口用于质子层面图,这一层面图的最低价格将不会很大。在探讨这些可能性时,重要的是诊断放射学家和治疗放射学家一起工作。
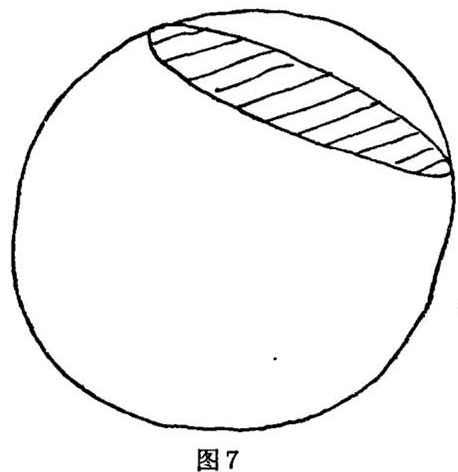
新近我对一定数学课题发生了兴趣,我将讨论这些课题但不涉及数学细节。我已经把Radon问题用CT扫描中通常给出的形式提出,即如果给出一个平面内所有线条的线积分,如何去恢复平面的函数。这可以推广到三维,如图7所示。这显示出了一个球体,其中的函数是明确的,和一个平面与这球体相交。假定给予的信息是所有与球体相交的平面的函数的积分,于是问题是“能不能从这些积分恢复这些函数?”。Radon提供了肯定的答复,并提供了求得函数的公式。发现这公式比二维的要简单一些,并且在核磁共振(N. M. R)成像方面而不是在X线方面可以应用。很容易在欧几里特空间内推广到n维,这已由Radon给出。在1960年前知道Radon工作的一定数学家把他的成果应用于偏微分方程学说上。他们也把他的结果推广到圆或不变半径的球体,以及某些椭圆体的积分上。推广到欧几里特以外的空间由一些人们例如Helgason及Gelfand等在六十年代时作出。
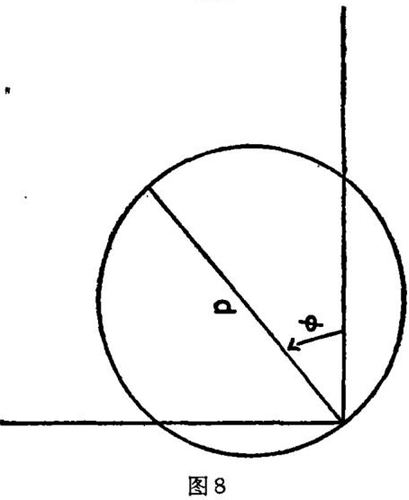
在我1964年的论文中我对一个问题,经过原点的可变半径的圆的积分提出了解,如图8所示。最近Quinto和我对这个问题得出了更为详尽的结果,推广到n维欧几里特空间,我们已应用这些结果得到达尔布偏微分方程求解的某些定理。我们的结果与Radon的结果有密切的联系,我们现在正试图发现一些更为通用的结果把关于一个表面族的Radon问题的解与另外一个表面族,即与第一个表面族有一定方式联系的第二个表面族的Radon问题解联系起来。
这些结果有什么用?回答是我不知道。它们将肯定产生偏微分方程学说方面的一些定理,其中某些将应用于核磁共振或超声成像技术,但这些当然无法肯定,也已经超出本题。Quinto和我研究这些课题的原因是因为它们在它们自己的范围内作为一个数学问题来研究而感到兴趣,而这一点本来就是科学所要求的。
在许多对我有益的人们中,我只能提出了部分。去世不久的R. W. James,教授F. R. S,Harvard回旋加速器实验室的主任,Andreas Koehler和我的家人。
_________________
* CT即计算机层面图