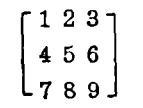
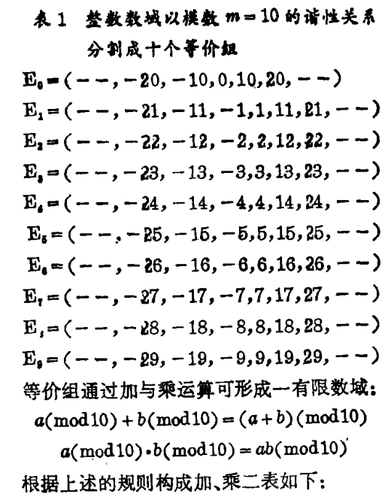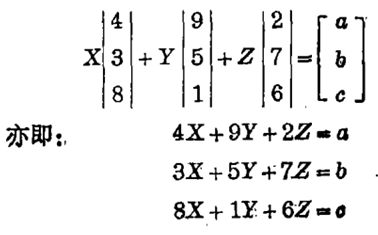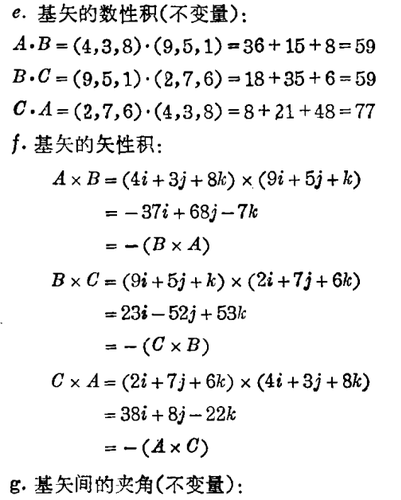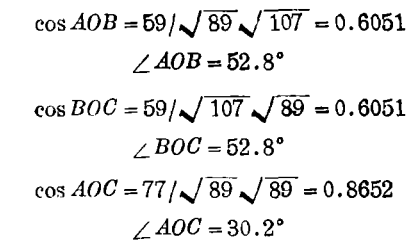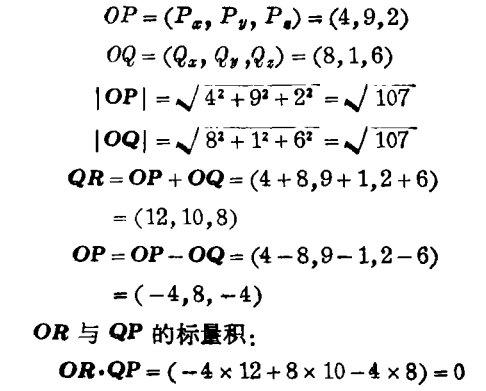洛书是我国早年在黄河洛水一带发现的龟甲，它上面刻有一到九的九个自然数的排列（如图）。对它的价值一直鲜为人知。美籍华裔学者焦蔚芳博士原系世界品名的金属材料科学家、1980年在美国组织爱灵顿理念书院，专门研究洛书的数学内涵，曾多次来我国讲学。他的有关洛书数学研究的第一篇论文——“焦氏洛书矩阵学说”曾载于本刊1987年5月号。本文为第二篇，曾在1988年8月发表于第五届中国科技史会议文集。

引 言

在对中国传统数学的探索中，可以发现一个“焦点性”的问题：“为何中国古数学家未能把几何学建立为数学中的一个独立分支？”回顾历史我们看到，中国古数学家往往倾向于数理和代数，他们在应用几何图形时，也注重于用度量和代数法来处理它们以求解决实际问题。在这方面，中国与古希腊的数学家显示出鲜明的对比。李约瑟（Goseph Needham）在其《中国科技史》一书中也曾论述过这一焦点问题，并认为这是中国传统数学之所以未能发展为现代数学的主要原因。上述的焦点还引出另一个重要问题：“为何中国古数学家经常以代数形式提出几何方面的命题？”当然，要全面探讨这些问题，将超出本文的范围，本文仅讨论其中的一点中国古代的洛书与现代抽象几何的关系/因为众所周知，洛书是中国的数学之源，而在洛书图阵的整数关系中是否含有抽象几何的现代概念？或是通过洛书图阵的结构可以建立这些概念。这将是本文的主要研讨目标和内容。

中国古数学家曾用“像”、“数”、“理”三字来概括数学研究的范畴。用现代数学观点来看，这三者正与几何、代数和数论这三大数学分支相对应。作者在洛书的数学研究方面也建立了相应的研究成果：其一是以代数学为前导，即“焦氏洛书矩阵论”；其二是以解析几何为前导，即本文——“焦氏洛书数字几何学”；其三是以数论为前导，论文即将发表，至于本文的重点则包括洛书空间的构成、洛书空间的特质，以及“焦氏洛书几何学”的基本命题。现分别叙述如下。

一、洛书空间的构成

自然界中存在着三个内在的数学实体：“空间”、“时间”、“数字”。从“空间”中，我们可以得到有关位置、方向、平行、垂直和几何外形等等的概念；应用“时间”，我们可以描绘有关运动、速度、频率、周期性和动力性等等的物理现象；应用“数字”，我们建立了计算、度量、有序性、算术运算和函数关系等等的数学方法。所谓“数学之科学”的主要内容就是研究上述三个实体之间的相互作用与内在联系，而其关键就是用数字（数学模型）来描绘空间（事物）与时间（运动）的关联。

数字是数学的根基，而数字的数学意义又可通过代数和几何这二条途径来表明，代数用符号和函数方程式来处理数字运算；解析几何则用坐标系统来处理数字的图示外形。代数符号化及运算与数字的关系正好跟解析几何中轴系与数字的关系相对应。因而代数函数可通过解析几何用图像来表示；反之、几何图像也可用代数函数来表示。这样，数字、代数、几何三者构成一种“三相循环”关系。换句话讲，代数与几何是数字的二种表现形式与应用方式。

基于上述概念，我们可以设想一个囊括上述关系的空间，并名之日“洛书空间”（Lo-Shu Space）。

1. 洛书空间的构成图解。 一个三维空间必须由三个独立的基矢群（坐标系）构织而成，在三维坐标系统中，矢量必由三个数量组成，张量必由三个矢量组成。根据这一概念，我们分别应用函数（多项式）、矢量和数字的三个三维空间的相互转变，建立起来一个“三相循环”所构成的空间，我们称它为“洛书空间”。图1示出三维洛书空间的构成图解。

2. 洛书空间的定义。 洛书空间是由一系列数字集合所构成的数学空间。这些数字集合的组成是由从0到9的十个自然数及其相互间的加、减、乘、除运算的结果，洛书空间的具体代表就是洛书矩阵。从洛书矩阵，我们可以开发出洛书代数；洛书几何和洛书数论这三门数学分支。而洛书空间本身自包涵有函数、矢量和数字三个次空间（图1）。

在自然界中，我们可将任一种均质现象的连续集合视为一个空间。宇宙本身就是一个非常复杂的且具有无限维数的空间。在数学上，我们采用自然数列作为建立诸如可数性、基数性、一一对应性等基本数学概念的基础。而洛书空间正是由自然数构成，由自然数本身所具有的、内在的、解析的、不需证明的公理来阐明，因而它代表了一切感性认识中最优先的一种数字集合。图1所示的三维洛书空间就是客观存在且亦可被人们的感官所觉察的空间。依此推演，自可衍生出n维空间。

二、洛书空间的特质

如果上述的洛书数学空间可以描绘自然界中的客观现象及显示物理世界的映像，它必须具有一些特有的性质以作为判定现象的指导推测。这些特质中最主要的是：

a. 洛书空间一定是一个线性系统，构成该空间的数学操作是加与乘。

b. 洛书空间是无限的，但是通过数学操作亦可变成有限（有定）的。

c. 洛书空间为连续的，但亦可被数学运算划分成许多互不连续的组合（Group）。

d · 洛书空间可由实数和虚数、有理和无理数组成。

e. 洛书空间并非一成不变，而是可以重复地膨胀与收缩。

f · 洛书空间具有均质、对称和平衡性。

g. 洛书空间能作周期性地运动或永不休止地变化。

h. 洛书空间具有量子化的特质。

可以说，洛书矩阵论、洛书几何学与洛书数论均由上述的特质演绎而成。因限于篇幅，本文仅扼要讨论洛书几何学中若干主要特质如下。

1. 洛书空间的线性本质。 洛书空间中的一切单元（Element）都必须满足于线性关系式：Y=mX+b。式中：X与Y为单元中的变数，m与b为单元中的参数。

该线性方程不仅可以描绘出自然数域（Field），而且也是由自然数域导出其他数域的基本方程。它的运算操作只有加和乘二种，因而满足上述特质a。基于这一线性方程，我们可在整数、实数、复数、有理数、无理数等一切数域的基础上构成洛书空间（符合于特质d）。

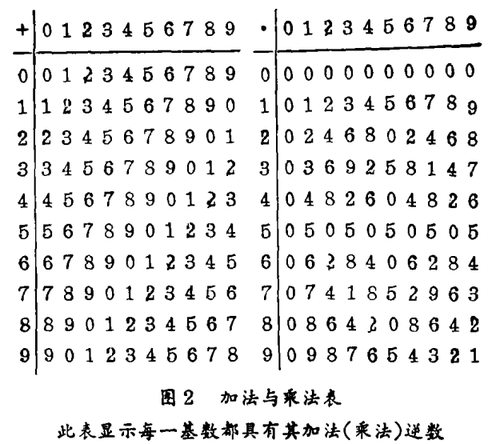
2. 在整数数域内形成洛书矩阵。 整数数域为十进制系统。十进制的独特表现形式在于只需用10个数字（0，1，2 … 8，9）即可表达一切数。（其中各数字的位置表示10的指数）。在十进制中，一切整数均可由上述线性方程来构成。此时，m为10的倍数，b为0至9中的任一数。或是以下列方程来表示：

Y=a_nxⁿ+a_n-1x^n-1+ …a₀

按照数学常规、零集合是一切集合的子集合，零以外的九个数字（1，2，3 … 8，9）可以组成一个数字集合，现称之为洛书数字集合。用这九个数字构成的3×3矩阵即洛书矩阵。洛书矩阵可以代表含有自然数域（N）、整数数域（Z）和实数数域（R）的三维洛书空间。

对整数集合进行加与乘的运算处理后得到的无穷数域演示了洛书空间的连续与无限性（即特质b，c的一个方面）。

3. 将整数数域分割成等价组（Equivalence Classes）。 取线性方程的逆置形式：X=(Y-b)/m，并定义：

f(X)=(X-b)/m 或： X≡b(mod m）

右式为谐性模式（Congruence Modulus），式中m为模数，b为余数。其意义为X对余数b与模数m存在“谐性”关系。亦即X与b系两个等价整数（因为它们被模数m除后的余数相同）。这样，通过谐性模式中的减与除二个运算操作可以实现谐性关系，当模数m=10时，可以把十进制的整数数域分为十个等价组。代表这十个等价组的基数即0，1，2…8，9这十个数字。等价组又名余值集合（Quotient Set），并以数学式Z/R₁₀=E₀，E₁，… E₈，E₉来代表如表1：

等价组的构成表示了数域的隔离性与有限性，亦即演示了洛书空间的不连续性与有限性（特质b，c的另一方面）。

三、建立洛书几何的前言

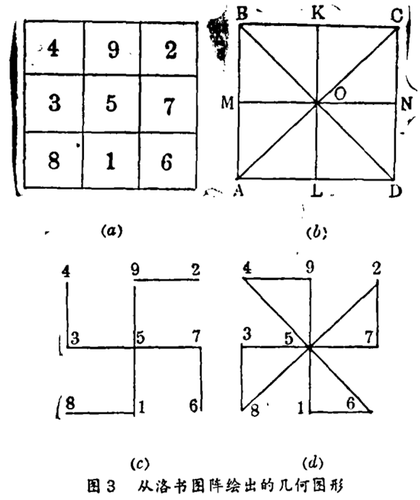
1. 洛书图阵的对称性。 如果在数字结构上我们说洛书是一个“幻方”^[5]（图3a），那么在图形方面我们可以看出它具有正方形的对称性（图3b）。

由图中得出：正方形ABCD相对于以O为中心以90°为倍数的角度旋转时总是对称的（四个位置），此外，它相对于对角线AC，BD和垂直线KL，MN也是对称的。（以上共八个对称度。）基于数字间的对称和均衡关系，从洛书图阵中还可以作出很多几何图形，图3c与3d中的卍字形和风车形为其二例。

2. 洛书基矢。 将洛书矩阵中的三行或三列作为三个空间矢量，并将它们作为三维坐标系统中的基矢（Base Vector），是为洛书基矢。定义如下：

四、焦氏洛书数字几何学基本命题

1. 洛书坐标系统。

a. 在基元（Unit Base）基础上形成的洛书坐标系。

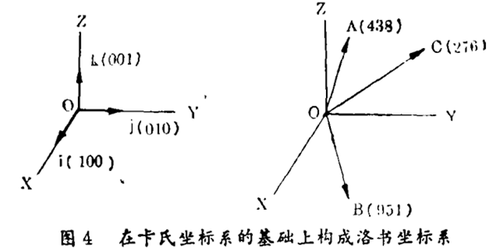
将洛书图阵中的三行（或三列）三元数（Triad）当作三个基点，并如上面所述构成三个洛书基矢（即洛书坐标系中的基元）。对照卡氏（Cartesian）坐标系可构成洛书（Lo-Shu）坐标系如图4所示。

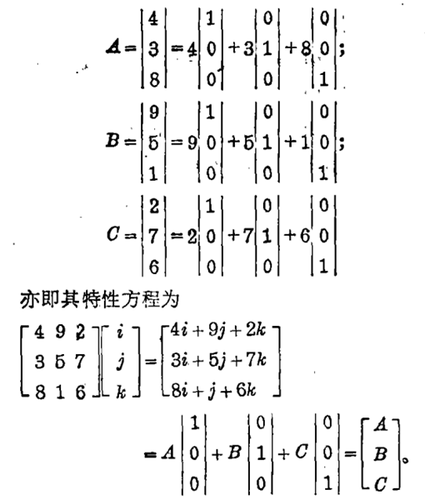
b. 洛书基矢的形成公式和特性方程。

洛书基矢的形成公式可从基元矩阵的线性组合（Linear Combination）原理来推导如下：

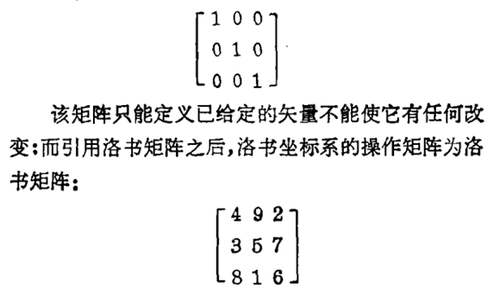
基于矩阵关系，我们看到卡氏坐标系的操作矩阵（Operation Matrix）即众所周知的单元矩阵（Identity Matrix）：

而由于洛书矩阵所特有的运转特性［4］，它不仅可以改变其所定义的矢量的大小，而且能引起其性质的改变。

c. 洛书空间的矢量群。

定理：洛书空间的任一矢量［a，b，c］是由三个基矢A=(4，3，8)'；B=(9，5，1 )'；C=(2，7，6)'线性组合而成。

证明：假定该线性组合方程为XA+YB+ZC

我们有：

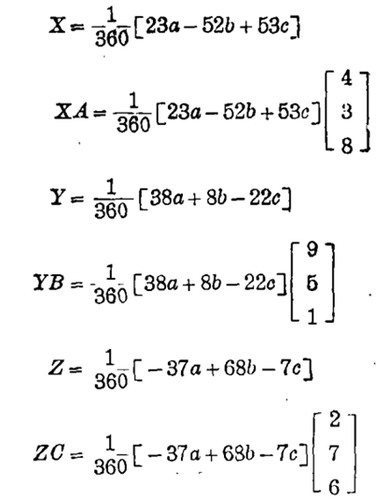
解联立方程组得：

用同样的代数转换解联立方程的方法得

（2）Xe = QX_a式中Q为洛书逆矩阵：

很容易证明Q=P^-1。此外，很有趣的是Q亦为一幻方，其中每一个三元数的数字之和均为24。

f. 二种坐标相互转换的结论。

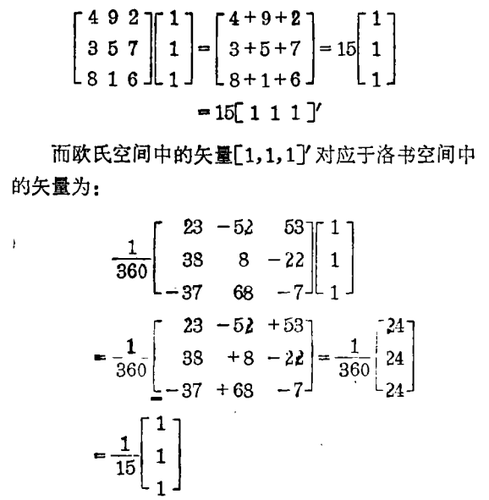
从上述对卡氏坐标与洛书坐标的转换研究中，我们可以得到洛书矩阵在数学操作中产生的特殊效果。举例而言，洛书空间中的矢量[1，1，1]'对应于欧氏空间中的矢量为：

由此可看出洛书矩阵的运转可导致矢量的膨胀或收缩。

2. 洛书坐标系中基矢的数量特性、几何特性及其不变量。

设A，B，C为洛书矩阵中三列数字所分别代表的坐标点；A'，B'，C'为三行数字所代表的坐标点。它们的坐标、位矢、矢长、方向余弦和其他不变量可用下列基本数学公式来计算［6］。这里，我们主要列出基矢A，B，C的各种参量（A'，B'，C'与之类似）。

a. 基点及其坐标（见图1）：

（A）=（4，3，8） （B）=（9，5，1） （C）=（2，7，6）

（A'）=（4，9，2） （B'）=（3，5，7） （C'）=（8，1，6）

b. 基点的位矢及其分量：

OA=A=（4，3，8）    OA'=A'=（4，9，2）

OB=B=（9，5，1）    OB'=B'=（3，5，7）

OC=C=（2，7，6）    OC'=C'=（8，1，6）

c. 基矢的矢长（不变量）：

3. 洛书空间的点网络（Point Lattice）。

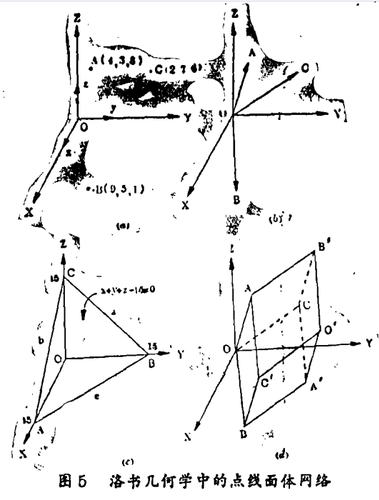
a. 洛书几何学中的点线面体网络结构。

在基础几何学中，三维空间是以点线面体来描绘的，其中以点作为空间的单元。在某一已给定的线性直角坐标系或斜坐标系中的整数点的集成（Integral），即空间网络（Space Lattice）。在图5中列出了洛书几何学中的点线面体网络结构。根据这一图解，可以了解洛书数字怎样成为点、线、面、体几何图形，以及它们的一些其他方面的物理涵义。

b. 洛书的三角形平面，洛书的三角形平面如图5d所示，平面的普遍方程为Ax+By+Cz+D=0。在本文后面的定理中将证明该方程的解为x+y+z=15，亦即平面上每一点的坐标（x， y，z）之和为15；从原点到三角形各顶点的距离也均为15。此外，又可解出该平面的截点方程为：

x/15+y/15+z/15=1

该方程明确显示了洛书平面的特点，并对洛书图阵中每一组三元数之和均为15，作了几何学上的表达和解释。

c. 洛书平行六面体。洛书平行六面体如图5 d所示。它由矢量OA、OB、OC（基矢）组成其三根轴，由基矢的平行线及基矢的和构成其棱与对角线。洛书平行六面体的体积可由三个基矢的标矢积来得到。即V=A ·（B×C）。洛书平行六面体是十分令人感兴趣的，它的其他特点将在以后叙述。

d. 洛书空间的几何结构总论。根据作者的研究结果，洛书空间的几何外形是由运转中的洛书矩阵本身的代数结构所决定的。当洛书矩阵取其自然形式：

时，它产生一个初始的几何外形，其体积为零单位；当采取其本体形式如图3a所示时，它产生一个稳定的几何外形，其体积为360单位。

这样，洛书空间的几何外形将随着运转中的洛书矩阵的结构变化而不停地转变，因而洛书空间为一周期性的运转空间（符合于前文的特质e及g）。

4. 洛书几何学中的数字标量场、梯度和矢量场。

a. 洛书平面场几何学。将洛书图阵视作为平面图形，图6a为洛书的数字标量场，显示了不同位置上的数字分布情况，根据数字间的线密度（Line Density）这一概念，引出如图6b所示的梯度矢量场。图中梯度矢量的方向用箭头表示，大小则用引线上的数字来表示。更有意义的是上述的梯度矢量场可以演示矢量加法的三角形定理。再进一步，可以发现图6b所示的矢置场也显示了均质、对称和平衡等特性（洛书空间的特质f）。这正是洛书“场几何学”（Field Geomeery）的精义之一，也是洛书矩阵的独特性质之一。

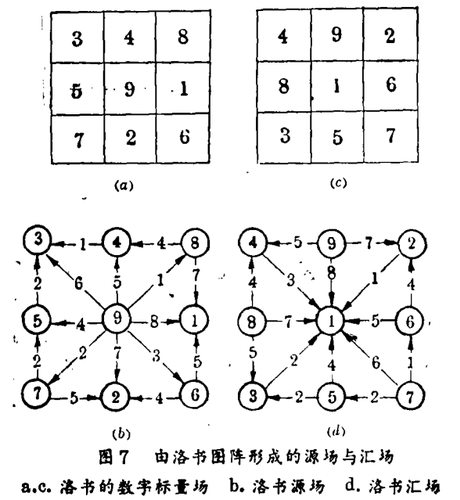
研究洛书梯度矢量场的“流动”性质，又可得到洛书的“源场”与“汇场”如图7所示。

用9作为洛书的中心数字（图7a），这样得出的矢量场具有从中心流向一切其他点的性质，这就是洛书源场（图7b），中心点成为点源，依次类推、用1作为中心数字（图7c），得出的矢量场具有向中心点汇集的性质，就是汇场（图7d），中心点即点汇。

建立于数字线密度基础上的洛书平面场将是一种统一场。它不仅是洛书空间的一种几何形式，也将为演示物理世界中的各种场提供新的数学基础。

b. 洛书几何学的空间矢量场。

将洛书矩阵看作为均质条件下的应力矩阵。图8为三维应力矩阵与洛书矩阵的对照。由对比关系得下式：

这里可再度得到这样一个结论：洛书空间矢量场可以完善地说明物理现象中的均质性、对称性和平衡性。

众所周知，应力矩阵为一个二级张量，洛书矩阵也可被看作为二级张量，并有可能用来表示诸如应力、应变、热传导、导电性等多种物理性质。

5. 洛书几何学中的标量积空间（Scalar Product Space）。

数学中二矢量α与β的标量积公式为：

α · β=α_xβ_x+α_yβ_y +α_zβ_z =|α| · |β| Cosθ

将此式应用于洛书空间的六个基矢（A, B，C，A', B'，C'）可得到洛书几何学中标量空间的若干特性。

a. 平行性。基矢间的平行性有下列二种情况：

情况Ⅰ。两基矢α与β的平行性可由α、β与第三基矢γ之间的内夹角相等来证明。其条件为

如   |α|=|β|；α · γ=β · γ

则           α∥ β。

情况Ⅱ。两对基矢间的平行性可由该四个基矢α，β，γ，δ组成一平行四边形来证明。其条件为

如｜α|=|γ|；|β|=|δ|；α · β = γ · δ

则           α∥ γ；β∥ δ。

b. 平行六面体形成特性。已知洛书平行六面体的体积为三个基矢的标矢积（Scalar Triple product）（亦即洛书矩阵的行列式值D）。根据这一特性，作者发现洛书基矢的标量积与矢量积之间有下列关系：

定理Ⅰ。如果两对基矢有相等的标量积，则矢量积的矢长相等。

如     α · β = γ · δ

则     |α×β|=|γ×δ|

例如： A · B'=（4，3，8）·（3，5，7）=83

C · B'=（2，7，6）·（3，5，7）=83

c. 用六个基矢的实际数值来演示洛书几何学中的标量积空间的特征。

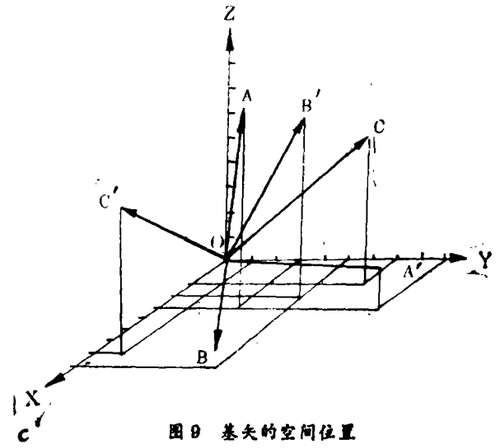
六个基矢的矢长示于本文四、2、之c段，其空间位置示于图9。

我们看到，没有任何三个基矢是在同一平面内的。

由于交换律适用于标量积，因而六个基矢共有6×5/2=15种组合。这15种标量积空间的特征列于表Ⅱ：

五、洛书几何学中若干基本定理示例

这里给出洛书几何学中基本定理四例以说明洛书几何学的真实性。

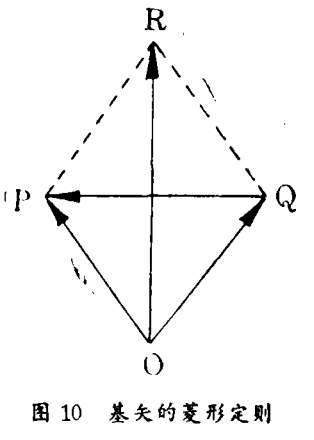
1. 定理1。任何二个等矢长基矢的和与差（均为矢量）必定相互垂直。（菱形定则）

证：在洛书矩阵中，有一对行矢量和一对列矢量各符合于矢长相等的条件。令其中一对行矢量为OP与OQ（图10）

∴       OR⊥QP

同样，可以用另一对等矢长的列矢量OP=（4，3，8）与OQ=（2，7，6）来证明上述定理。

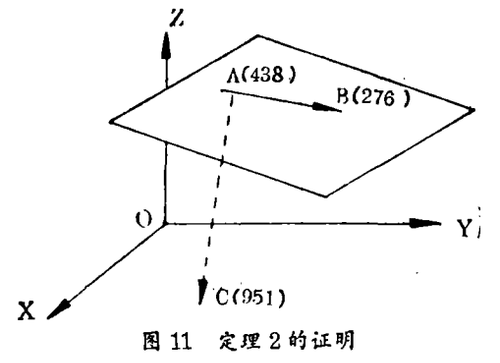
2. 定理2。在三维（R²）洛书空间中、给定三个非共线也非共面（且均非零矢）的点基矢A、B、C。如果以A与B为两个基点以形成一个平面次空间，在该平面中AB为一直线矢量，则点矢C的方向垂直于AB。

证：在洛书空间中，取三个列矢量，其坐标点分别为A=（4，3，8）；B=（2，7，6）；C=（9，5，1）如图11。

A，B与C为非共线矢量亦非共面矢量。A与B为两个等矢长基矢，因而可以被用作为基点以形成一平面次空间、在该平面内AB为一直线矢量。

AB矢量：AB =B - A=（2，7，6）-（4，3，8）=（-2，4，-2）

∵ C · AB=（9，5，1）·（- 2，4，-2）=9（-2）+4×5+1（-2）=0

∴ C为AB的垂直方向矢。C丄AB。

同样，我们亦可用三个行矢量A=（4，9，2）；B =（8，1，6）；C =（3，5，7）来证明上述定理。

3. 定理3。洛书矩阵为洛书空间中的平面的标准方程AX+BY+CZ+D=0的一种表达方式。

式中A，B，C为系数，D为从原点到该平面的垂直距离。

证：将洛书矩阵中的三行数字看作为空间中的三个点：P =（4，9，2）；q=（3，5，7）；r=（8，1，6），由于三点决定一平面，因而这三个点当在满足下列联立方程式的平面之内：

即前文四3b中所述的洛书三角形平面方程。

4. 定理4。所有的3×3阶幻方在实数域内构成一矢量空间。

证：令M为所有的3×3幻方集合，并假定：

A=[a_ij]∈M；B=[b_ij]∈M           （1）

加法操作可定义为：

a_ij + b_ij =(a+b) _ij；i，j=1，2，3   （2）

从（2）式可得出结论：二个幻方之和亦为一幻方。于是M在加法操作的情况下是封闭的。由于实数在加法运算时服从于交换律和结合律，所以在M集合中，加法也是可以交换和结合的。

如：                   A+B=B+A

（A+B）+C=A+（B+C）        （3）

各元素（Element）均为1的矩阵也是一幻方。各元素均为零的矩阵0=0亦即M集合中的零元素。

A+0=A                     （4）

矩阵                   A=[a_ij]                       （5）

的负矩阵为            -A=-[a_ij]                     （6）

注意此处由于A是一幻方，-A亦为一幻方，且

      A+（-A）=0                 （7）

A与实数相乘可定义为

αA=[αa_ij]

式中在标量乘之后M仍是闭合的，由此得