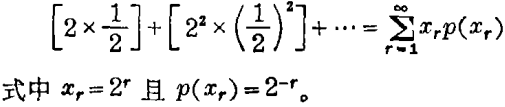概率论与统计学的大多数结果似乎完全违反常识。有时由于政治家们不懂得这一学科,以致浪费公款和损失生命。
许多人认为统计学是一门诡术,它的结果是不可信的。迪斯雷利(Disraeli)的并非新鲜的评论:“谎言,荒天瞎话与统计学”已在公众想象中根深蒂固。至于统计学这门学科为何落得如此狼藉的名声还不清楚。其理由之一,也许在概率问题上,常识和直观都是蹩脚的向导。
概率论的许多结果似乎违反常识——它们是“反直观的”。由于概率论的悖论与个人特有的主观评价以及历史时期有关,所以立刻又产生“谁的直观?”这样一个问题。我们就来说明概率论的概念已被所谓圣彼得堡(St Petersburg)悖论演变到什么程度。这个悖论在18世纪由瑞士数学家贝努利(Bernoulli)论述过,它是在假借机会游戏的赌博中提出的一个统计学问题。(赌博曾经是概率论发展初期的有力促进因素!)
这个问题就是在抛一枚钱币直到出现正面为止的赌博中,确定赌徒应先交付给银行家多少赌注以获得参加赌博的权利。如果赌博结束时抛钱币的次数为N,那么银行家就付给赌徒2N卢布。现代分析表明,赌徒赢的数学期望是无限的,它是一个无穷级数的和,这个级数的每一项都是1,可表示如下:
圣彼得堡悖论在18世纪以前的确是荒谬的,因为不具有有限的参加费使对于银行家和赌徒两者都是公平的想法是极端违反直观的。当然,今天我们可以用数学理论使之合理化。
然而,在最简易的水平上,概率论不仅是一个数字计算问题,而且也很像是运用逻辑的智力测验问题(见附一)。解答这一类问题时,熟悉有关的原理是重要的:在附一所提到的民意测验中,当询问需要懂得样本性质的问题时,统计学家比艺术系毕业生解答得更好。例如,怎样正确地回答下面的问题:考虑在每天出生的婴儿中有百分之七十以上是男孩的天数,这些天数很可能经常出现在大的产科医院呢,还是在小的产科医院?非统计学家是没有把握的。
附一 概率逻辑①
在一个简易的水平上,我们考虑概率与逻辑的混合问题。如果有人在桌面上展示四张牌,它们分别用A,B,1和2标记,并且说:“元音字母的反面有偶数。”他们需要翻转哪一张牌或哪几张牌来测验所给命题的其实性?在一次大学毕业生的民意测验中,大多数人回答“A和2”。然而,正确的答案是“A和1”——指出这一点每个人就会立刻明白。
答案是小医院。理由如下:每出生一个婴儿不是男孩就是女孩,并且每次生男或生女的概率大致相等。在出生婴儿的大样本(也即在大医院)中,男孩所占的百分比总的说来很可能比小样本(小医院)更接近于期望值(约为51.5%)。
凯恩尼曼(Kahneman),斯洛维克(Slovic)和特维尔斯基(Tversky)在他们所写的《在不确定情况下的判决:直观推断与偏见》(《Judgement Under Uncertainty:Heuristics and Biases》,剑桥大学出版社,1982)一书中提出类似这样的错误是很可能产生的、主要是因为人们还没有认识到一些原理的适当应用(这里指抽样理论)、而不是因为他们未完全掌握这些原理。在概率估计中这类错误是很常见的,但是在估计一个特定结果的概率时,当许多人普遍地而不是偶然地犯了同样方面的错误后,人们便开始提出一个重要的问题。
作为估计概率时犯有普遍性错误的例子,我们来考虑这样一个事实。有一批人,他们的生日随机地分布在全年之中,要使他们至少有二人生日相同的机会大于生日都不相同的机会的最小人数仅需23人。有人认为(虽然我还没有证实这一点)由那些不熟悉这一结果的人来推算,这个最小人数一般地将大于23人,或许还要大得多。
人们在估计概率和危险率时犯有普遍的主观的错误可能对社会政策具有相当重要的影响,我将在后面讨论这些问题。但是为了更具体说明问题,下面列举我作为医学统计学家在危险地区工作时所经历的一些例子。由于反直观的事情是随时间和地点而不同,故有些例子可能对某些人是一目了然的,但绝非每个人都能这样一眼看出。
混淆的因素
在统计学中最常见的“混淆的因素”之一是年龄。考虑两个城市死亡率的比较,我们把一个城市称为克罗姆维尔,另一个是海滨城市,称它为斯诺金,它们都约有十万居民。斯诺金每年有1500人死亡,克罗姆维尔每年仅约1000人死亡。这能证明克罗姆维尔是比斯诺金更有益于健康的地方吗?实际并不如此。人们完全可以相信、就任何年龄来讲,克罗姆维尔的死亡率实际上都超过斯诺金的死亡率。克罗姆维尔是最近建立的新兴城市之一,因此有许多年轻人的家庭,而海滨城市斯诺金则是富裕的退休人员颐养天年的理想之处。在斯诺金城市里,表面上过高的死亡率仅仅反映这个城市有更多年老的居民,对于这种年龄的人,死亡率自然是高的。用统计学家的语言来说,年龄是一种混淆的因素,在能够做出公正的比较之前,需要将年龄标准化。
许多混淆因素不太明显——或者甚至是未知的——因此更为危险。就拿两种不同的治疗方式A和B的治愈率来说。一次调查表明,接受治疗方式A的人中大约有一半的人痊愈,而接受治疗方式B的人中大约只有四分之一痊愈。看来好像方式A大约是方式B的治愈率的两倍。但是如果有特性的人不是“随机地分配”给每一组又怎样呢?假定在一组中具有“习性X”(习性X可以是任何特性,但未必是非常有害的特性)的人比另一组多得多呢?对于A优于B这一结论,我们必须限制到什么程度?
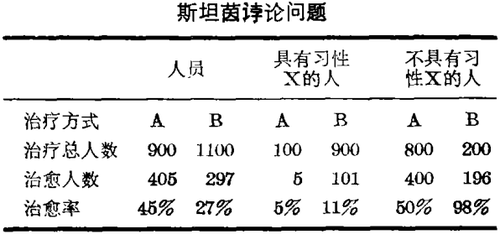
原有的结果被混淆因素完全破坏了(见下表)。由X习性和非X习性的人在接受不同治疗方式的人群中分布不均匀而产生的这种效果有时称为斯坦茵(Stein)悖论。
假设具有习性X的人不是随机地分布于A. 和B两组内,那么我们对于治疗方式A是治疗方式B的治愈率的两倍这个结论需要修改到什么程度呢?上述数据表明对于具有习性X和不具有习性X的两组,治疗方式B优于A的结果,这就完全推翻了原来的结论。
在流行病学的分析上,这个悖论是难题之一。诚然,一般说来无法肯定不存在我们尚未认识的某个重要的因素,但是它的未被察觉到的作用却完全有可能推翻所得到的结论。在广泛接受吸烟对肺癌的作用之前,人们最初关于肺癌死亡率的研究提供历史上的一个例子。在供作肺癌研究的各种人群中,有无吸烟的比例差别很大。由于后来已明白(吸烟致癌)的道理,故我们现在能够识别有偏见的研究,虽然这种偏见当时并不明显。
惊奇的原理
其他反直观的结果出乎意外地与条件概率的概念有关,举例来说,条件概率就是将要发生的事件B的概率依赖于与之有关的并已发生的事件A的已知概率。
设想有两个人埃里克和弗雷德,他们在等待提供“15分钟服务”的一条线路上的公共汽车。由于交通拥挤,故公共汽车不是精确地按照15分钟间隔到达的,而是随机来到。然而,经营者(普阿松(Poisson)汽车公司)却能够提供平均15分钟到达一辆的服务。
与我们在前面所说过的赌博的方法相一致,弗雷德对埃里克提出一个对等赌钱的赌博,如果公共汽车在10分钟内来到,他就赢了。他知道这路汽车是15分钟服务一次,因此他很快算出平均等待时间是七分半钟。埃里克同意了,并握手确定。过了10分钟汽车仍未到达。弗雷德输掉了他的赌钱——那么,他输在形势对他不利吗?下面的推理指出实际上赌博对埃里克有利。
因公共汽车是随机到达的,故埃里克和弗雷德所面临的等待时间事实上不少于公共汽车之间的平均时间即15分钟。比较不断地抛掷一枚钱币的情况:钱币出现10次或100次正面的事实并没有告诉我们关于抛第11次或第101次任何可能结果。同样地,当埃里克和弗雷德到达公共汽车站时,虽然在前班的公共汽车通过之后又过了一些时间,但是在普阿松汽车公司所提供的这一类服务之下,并不影响我们对埃里克和弗雷德将要等待多少时间的估计。如果这个分布是普阿松分布(见附二),那么在有限一段时间之后偶然事件的条件概率与无条件概率是相同的。这是因为普阿松分布具有所谓“无记忆性”的性质。仅当公共汽车以15分钟的固定间隔行驶时,他们的平均等待时间才是七分半钟。
附二 普阿松分布和普鲁士(Prussian)骑兵
普阿松分布是统计学中最常见的分布之一,其模型是定义在部分空间或部分时间上的事件可能出现的次数的分布。19世纪普鲁士骑兵事件就是它的最好例子之一。普鲁士骑兵有10个部队,在20年期间,每年骑兵被他们的马踢死的人数令人信服地符合普阿松分布的理论形式。
在任何一年、任一部队中,被马踢死的这类事件发生0,1,2,…次的概率,按普阿松公式可写为
p(x)=exp(-γ) γx(x!)-1
其中γ是死亡的平均数。据记载,每年在每个部认中平均有0.61名骑兵被马踢死。不难核对,在指定的部队和指定的年份里,不发生这类死亡的概率p(0)为0.543。
—个类似于埃里克和弗雷德在公共汽车站的模式可以用来描述事故的出现——这是特殊的论题——像白血病这样罕见疾病的地区发病率。相当多的地方和民族努力在诊断多发病方面进行投资,并提出各种可能原因,其中经常提到的有电离和非电离的辐射。事实上完全由于偶然性而出现多发病的情况要比人们所想象的更普遍得多。考虑一个由小居民区组成的地区,其中每个小居民区大约有3000个居民,这个地区平均每五年将出现一个白血病的病例。可是每个小居民区出现一个白血病的概率却小得惊人,是用n!n-n表示的,其中n是小居民区的个数(n!定义为n×(n-1)×(n-2)×…×2×1)。当n小到20时,表示式n!n-n给出的概率大约是四千三百万分之一。因此,白血病成为某种程度的多发病是确实无疑的。
几点说明
对于小居民区罕见疾病发病率的统计解释存在一个更加反直观的曲解。这可用西施科(Seascale)村庄充分地说明,这个村庄最接近坎伯利雅(Cumbria)的塞拉弗罗德(Sellafield)原子核加工厂。克拉夫特(Craft)和他的同事分析了北英格兰中675个居民区儿童恶性淋巴瘤的发生,西施科就是其中一个居民区。由于每个居民区儿童人口有变动,故用普阿松准则(所观察的病例个数服从普阿松分布时具有最小的概率,而这个分布中的参数就是该地区平均发病率)发现西施科的发病率居第一位。与此同时,当把该地区儿童的实际发病率进行比较时西施科却名列第三位。这样就发生很大的争论。
实际上,直观就是如此经常地——有时大得惊人地偏离客观事实。经过仔细检查可以看出,前面所提到的同一生日的琐碎例子与白血病分布这一颇为重要的问题恰好是相同的。在民主国家里运用舆论,可以对社会政策产生一个重要的但不是完全的影响。如果人们在估计危险率时有偶然性错误,那问题还不大,因为这些错误将会相互抵消。但是如果在估计某一危险性时存在普遍的和系统的偏见,这可能导致错误地分配保护人们免遭危险的珍贵资源。
辐射防护很清楚地证实这一点。拉塞尔(Russell)和韦布(Webb)指出以一定程度额外提供人们防护辐射方面,用在治疗辐射的经费比起用于核燃料方面少得多。换句话说,为保护人民对付辐射用于医学上的经费将比把同样的钱用于增加核电站的安全性方面能拯救出更多的生命。任何关于辐射剂量与它的效应之间的关系的争论也不可能改变这一事实。因此,逻辑上说,资源应当集中用于改善在诊断医学中使用X射线的那些人的保护上。另一方面,公众似乎认为核电站会构成更大的危险性。由此可见,资金被迫用于拯救生命和防止疾病的客观期望实际上较小的地方,而如果把同样的钱花费在另一种防护上收效会更大。
同样的论点也可以应用到其他重要的公共事业的决策上。例如,在1971年政府决定不采用保护儿童的药品包装意味着一个儿童的生命约值1000镑,另一方面,作为Ronan Point(某建筑机构)的部分倒塌的结果而改变建筑规则几乎同时意味着每个人的生命约值2000万镑。
所以直观的分歧确实存在,并且可以由于利害关系而提出一个原因。那么,人们为消除这些分歧能做出什么事情呢?
技术辅助手段,例如应用微型计算机,可能为某些地区提供一个解决办法。就拿临床诊断的技术而言,上一代的医生们遵循诸如“怪病少诊”的不确切的格言。现代的专家有方法,至少在理论上对于病症的各种混合有能力说出特殊诊断是正确的概率。所看到的数据是参照过去许多病例的特点而总结出的基本数据再利用贝叶斯(Bayes)定理后得到的。
上述几个例子说明了条件概率是多么难以估计,然而微型计算机对于使人类苦恼的失真的认识却完全不受影响!
[New Scientist,1985年5月]
——————
①原文这一段写得太简略。译者的理解是:原来有许多牌,正面为A,B,C,…等字母,反面为正整数。其对应法则是元音字母的反面必为偶数,而非元音字母的反面或为奇数或为偶数。所展示的A,B,1,2是其中有代表性的四张牌。前两张为正面,后两张为反面。显然,翻转“B和2”都无法验证所给命题的真实性。而翻转“A与2”或“A与B”或“B与1”也不能完全验证其真实性。唯有翻转“A与1”,从原命题与逆否命题两方面同时完全验证所给命题的真实性。