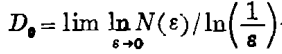引 言
非线性问题并不是一个近期才出现的新问题,也不是一个新的科学概念。但是,由于在确定论的系统中发现了混沌现象,极大地激发了人们去探索自然界和社会中存在的各种复杂性问题,同时逐渐改变了人们观察周围世界的思维方法。
由于复杂性往往与非线性紧密联系在一起,因此,在近20年中,从自然科学,工程技术甚至社会学各领域中,广泛深入地开展了非线性问题的研究,并且已经取得的成果显示了非线性研究在诠释丰富多彩的自然界、复杂多变的周围世界方面的深刻性,在哲学与方法论方面引起的深刻的变革。
60年代,混沌现象的发现,引发了人们对复杂性问题的研究,逐渐认识到非线性因素是这种复杂性问题的集中表现。通过简单的一维非线性映射,发现倍周期分叉现象的普适常数和时间演化中趋向混沌并且出现奇怪吸引子等非线性问题的共同特点。由此启发人们突破不词学科领域的局限性,从而形成了非线性科学这样综合性、交叉性的前沿学科。
相反,线性系统满足叠加原理,整体等于部分之和。数学的发展早已为线性系统的研究提供了包括线性代数、线性微分方程、傅里叶分析、线性算子理论和随机过程的线性理论在内的强有力的解析方法和工具,因此没有必要形成“线性科学”这一独立的学科分支。
正如非线性不满足整体是部分之和这一原理一样,非线性科学也不是非线性数学,非线性物理,非线性力学等等分支学科的总和。当前,人们已经发现,在自然科学的各个不同的领域内,各种系统有着共同的概念,非线性系统具有超越不同学科领域局限性的共同性质,非线性研究正在从范例的研究走向一个以探索复杂性为目标的新学科——非线性科学。
虽然科学知识的增长是爆炸性的,但以混沌现象作为中心课题的非线性科学的基本概念将会持久地影响自然科学的进程,成为继量子力学、相对论之后的一次新的科学革命。
近期非线性科学研究的主要内容
非线性问题的研究是极其困难的,过去采用在运转点附近线性化的方法,或者针对具体的非线性方程来寻求个别的解析处理方法。但是直至目前,对于非线性问题仍然没有完全系统的,类似于傅里叶变换那样的处理方法,更多的是集中于典型范例的研究和作某些定量分析。现仅根据国内外在非线性研究方面的近期进展和侧重点将其研究内容归纳为如下九个方面:
一、非线性映射的宏观特性
在混沌现象的研究中起着重要作用的是人们已经非常熟悉的一维非线性映射方程xn+1=f(α,xn)。其非线性迭代行为随控制参数α之值的变化而变化。以2n方式分叉的倍周期序列和Feigenbaum普适常数δ,是整个一类非线性映象都无例外遵从的,它与系统本身的具体结构的细节无关,迭代过程所呈现的特征是相同的,这已为从对流液体到非线性振荡电路的实验严格地证明了δ的普适性。
在越过α∞之后,xn的值呈现出不规则的图像,即混沌现象。通过改变α的比例尺度,可以使动力系统进入混沌区之后的细部层次构造显现出来。
其实在这些混沌区内,仍然表现出某种规律,在控制参数α的[0~α∞]区间内,有2n个倍周期分叉区;在[α∞~2]区间内,也有2n个混沌带,它们从左右两方面收敛于α∞,x的迭代值以2n的顺序落入这些窄带区内,在每个带内x的分布则是随机的。这就是所谓的无穷嵌套的自相似结构。
这类迭代过程表达了离散时闻演化过程(n为tn,Δt=1),由于存在非线性(虽然是很简单的),使这类一维映象都不能单值地确定它的逆映象f -1(α,xn+1),非线性将导致系统的耗散结构。所以,可以把一维非线性映射的迭代过程看作是单变量耗散系统的不可逆演化过程。
二,混沌与分形
我们已经看到,在确定性系统中出现了不规则的、非周期的、错综复杂的、具有自相似结构的非线性现象。与迭代过程相比,人们更关心的是由非线性微分方程描述的动态过程的演化特性。
1961年劳伦茨(Lorenz)根据大气运动的实际情况,设定了具体参数,通过计算机对描述基本大气环流运动的简化模型进行数值积分,变量随时间演化的数字计算结果表明初始条件只有千分之一误差的二组计算结果却造成了其后完全不同的演化过程。初始条件代表在起始时刻对系统所作的测量,测量越精确,观测者所获得的关于该系统的知识就越多,如果初始条件的微小变化引起的运动轨迹的改变也是微小的,那么初始条件所包含的信息将保留下来。因而可以对系统的动态过程作出预测,这时我们可以说系统对初始条件是不敏感的,相反,劳伦茨模型中初始条件的微小变化造成了轨线的巨大变化,初始条件包含的信息由于指数型发散而丧失,这时便不能预测系统长时间演化的行为,我们可以说系统是敏感初始条件的,失之毫厘,差之千里。
劳伦茨由此得出结论:“任何具有非周期行为的物理系统,将是不可预报的。”突破确定论长期禁锢的新的科学概念就这样诞生了。
在劳伦茨模型中不稳定的解将使轨线族之间任意相邻二条轨迹以指数方式发散,但是流体的动力学粘性将使系统在演化过程中耗散能量,运动轨迹将向吸引子收缩,要同时满足这二者,则只有通过伸缩与折叠变换,才能使指数型发散的轨线族维持在有限范围的吸引子上。伸缩变换使诸轨线在相空间中密集和遍历,折叠变换则使吸引子具有层次结构。同时,伸缩变换使初始条件的微小变化增大,折叠又使相距很远的轨迹会合,丧失了初始条件所包含的关于系统的信息。因此,伸缩与折叠变换是一种混沌操作,这样形成的吸引子称作混沌吸引子或者叫作奇怪吸引子,它高度敏感初始条件,因此具有奇怪吸引子的系统的长期演化行为是不可预测的。
人们惊叹劳伦茨奇怪吸引子的和谐与形式美,犹如蝴蝶的翅膀。谁又能预言,一只蝴蝶在巴西扇动翅膀不会在得克萨斯引起龙卷风呢?
当我们观察映射和奇怪吸引子的复杂图形时,已经隐隐约约地感觉到,这些曾经是陌生的图形是不能用我们熟悉的欧几里得几何学方法来描述的,在平直的欧氏空间中,点、线、面、体和由它们构成规则的几何图形都有整数维和测量其大小或几何性质的特征尺度。测量的对象不同,采用的尺度单位也不同。既不便用尺丈量地球又不宜用寸测原子,前者失之太短,后者得之过大,所谓“夫尺有所短,寸有所长”就是这个意思。
然而,具有无穷嵌套的自相似结构的映射图形和奇怪吸引子的复杂形态,无论怎样变换观测的尺度,局部仍然保持了整体的性质,特征尺度的作用失效了。
这种在尺度变换之下,图形的自相似性不变,换句话说,图形的复杂结构不变的特点就是无标度性。
如何刻画这一类几何图形呢?
曼德勃罗(B. B. Mandelbrot)提出了分数维的概念,建立了分形几何学,从而完成了一个科学概念的转变。他把人们的思维从欧几里德几何学框架的长期禁锢中解脱出来,又重新回到创造出无数绚丽多彩的分形结构的大;然之中。雷鸣闪电形状,蜿蜒曲折的海岸线,令人神往的云街,起伏的沙丘,树叶枝干的外形结构,美丽的雪花冰晶……都是分形的实例。
不能用整数维刻画的形状,无论怎样放大来看,它都和原来那样复杂(当然,是在统计的意义上),用分数维度量就意味着完全否定了分形的平滑程度,分形是处处不可微分的,漂浮在液体中的花粉形成的布朗运动是处处连续而处处不可微分的。因为在尺度变换下每一个层次上的细节放大后都是布朗运动,它具有统计意义上的自相似性,相反,特征长度意味着物体形状具有的平滑程度,它平滑了小于特征长度的细节,但保留了整体的特征。
我们熟悉的是经验维数,或者说是拓扑维数,用d表示。这种维数的特点是若用n维的测量单元1n去测量某个d维几何形状时,只有n=d,测量结果才是有限值,若n<d,测量值为∞;若n>d,则为0,这样测得的是整数维。
实际上早在1919年由豪斯道夫(F. Hausdorff)引入的维数的严格定义允许出现分数维数。其他几种定义,如信息维、关联维等等,虽然在数学上是很严密的,可是实际应用却各有局限与不足之处,比较简便的方法是以半径为ε的D0维球去包覆分形体,当t→0时确定包覆所需球的最小个数N(ε),再由公式
计算分维。
有了分数维,就可以刻画自相似结构和奇怪吸引子的几何特性,对它们的复杂程度给出定量的比较。但分数维并不容易计算,就奇怪吸引子的分类和系统的时空演化过程而言,还需要引入指数作为刻画非线性系统动态特性的一种有效方法。李雅普诺夫指数入λ<0的方向,相体积收缩,运动稳定,且对初始条件不敏感;在λ>0的方向轨迹迅速分离,长时间动态行为对初始条件敏感,运动呈混沌状态;λ=0则对应于稳定的边界,初始误差既不被放大也不被缩小。因为λ>0表示系统的动态过程在X取值方向是不稳定的,而λ<0则表示系统在λ取值方向是耗散的,这两种因素对抗的结果就如同前面曾说过的伸缩与折叠操作,形成奇怪吸引子的空间几何形状。
作为分数维概念的具体应用,也是作为数学中的反演问题,可以通过对某一复杂对象实际观测的时间序列数据重建该系统的动力学,自1981年泰肯斯(Takers)的论文发表以来,许多研究人员试图解决这个问题,已经提出了许多办法,不过都存在许多局限性,仍处于发展的初期。
三、动力系统的时间反演问题
从牛顿的伟大著作《自然哲学的数学原理》发表至今,300多年来,科学已经经历了两个关键时期,一是牛顿的经典力学体系,它支撑在一个均匀的、没有演化的静止的宇宙模型之上,物质、空间和时间是没有内在联系的,天体的运动,日月星辰都按“上帝”指定的轨道周而复始,未来包含在过去之中,动力学系统的行为是可以预测的,自然界的法则由决定论支配。二是爱因斯坦的相对论的宇宙模型和四维空间,物质和时间紧密地联在一起,空间与时间就是由物质产生的。自然法则是简单、美丽、和谐的统一,未来是可以预测的,随机性引入科学是我们无知的表现。
现在我们正在步入第三个关键时期,不可逆性遍布于自然界和人类社会的许多方面,正在引起空间、时间和动力学概念上的巨大变化,时间与演化联系在一起。正如当年爱因斯坦把光速C是普适常数作为自然界的一个基本事实一样,热力学第二定律将假定为一个基本的物理事实,熵的增加定律和隐含的“时间之矢”的存在意味着空间与时间的对称破缺,未来并不包含在过去之中,这是一个开放的、演化的世界。
经典力学的求解问题原则上可以归结为寻找正则变换或者运动积分。但遗憾的是动力学中可积系统只是极少数个例,况且不可积系统中随机情况又是普遍的,这又增加了经典力学的困难,本世纪之初,庞加莱对天体力学中不确定性的预见和开创的相空间描述方法推动了经典力学的发展;60年代前后由柯尔莫哥洛夫,阿诺德(V. I. Arnold)和莫泽(J. Moser)等人相继研究了哈密顿系统的可解性,也就是可积性。他们取得的结果被世人称之为定理,理论断言:动力系统(当然是确定论的!)可以导致随机运动(混沌的!)。这对经典力学的发展起了关键性的促进作用。之后,由于普里高津提出了动力系统的耗散结构和演化的哲学观点,把动力学的研究与物理学中的艰难的时间本质问题的研究联系起来,企图消除动力学描述与热力学描述之间的对立。由此,经典力学的研究进入了一个新的发展阶段。
到此我们已经看到,牛顿创立的经典力学体系,尽管是时间反演t→-t不变的,在动力学框架内时间是对称和没有方向的外界参数,但是我们仍然看到了动力学系统不可积时出现了随机性和混沌。因而统计的描述、系综的概念架起了连接动力学与热力学的桥梁。
热力学是通过熵这一概念与时间的本质紧密联系在一起的,牛顿力学描述简单物体的运动与热力学描述复杂体系的运动之间一个本质的差别是它们的时间演化行为。在牛顿力学体系中,空间是均匀的,时间是对称的,运动在时间中保持不变,过去与将来是等价的,运动是可逆的。然而,热力学研究具有大量自由度的复杂体系,它的宏观运动是不可逆的,一个初始具有不均匀温度分布的物体通过热传导总是自发地、单向地趋于一个均匀分布的温度状态,同样,一个初始不均匀的浓度分布状态必然会自发地、单向地趋于均匀分布的平衡态,如果进行时间反演变换,将t改为-t,则意味着单靠热传导过程或扩散过程温度或浓度可以自发地从均匀状态发展到某种不均匀状态。水中的一滴均匀扩散开来的墨水可以自发地重新聚集起来,但是自然界中不存在这样的自发过程。因此,时间的反演是不成立的。热传导和扩散过程是不可逆的,状态的演化发生在单一的时间方向上。
这样,热力学第二定律表明了如下一个事实,不可逆过程导致一种时间的单向性。正的时间方向对应着熵的增加。这里的问题是:热力学描述与经典力学描述之间的对立或者说多粒子体系的复杂运动与简单物体的运动在时间发展行为方面的差异如何统一起来,怎样统一起来?
普里高津认为,应当把熵增加原理与它所隐含的时间之矢的存在作为自然界的基本事实。同时,我们把物理世界描绘成一个“半群”才是有意义的。未来对应着t→+∞而不是t→-∞。他建议熵作为一个选择原则,它不能从动力学体系推演出来,而是一个客观事实,如同量子力学中的泡利(W. Pauli)不相容原理基于客观事实一样。
在非线性科学中之所以把时间问题作为一个重要的研究内容,不仅仅是时间广泛存在于一切自然科学之中,而且也是因为时间这个量把自然界;社会与人类活动联系起来,排除观测者及其影响作用的是牛顿力学体系的理想情况,这个理想情况在现实中是不存在的。
此外,经典力学与热力学之间的对立(当然还包括生物学的进化在内),微观可逆过程与宏观不可逆过程之间的对立,皆起因于时间反演问题,研究时间反演问题是深入理解混沌现象的关键之一,也是把确定论与随机理论统一起来的关键。
时间之矢曾经使多少伟大科学家感到困惑,也许混沌现象和时间问题是世纪交替之际向人类智慧提出的挑战吧I
四、自组织与耗散结构
在自然界中有两大类有序结构,一类是像晶体中形成的规则有序结构,或者像冰晶、雪花的规则结构,这是人们非常熟悉的。即使在孤立的环境中和在平衡条件下也可以维持,不需要与周围环境进行物质与能量的交换。这类在自然界中到处可见的有序结构——平衡结构,可以用玻尔兹曼有序原理进行解释:另一类可呈现出宏观范围的时空有序,但只能在非平衡条件下通过和周围环境进行物质和能量的交换才能维持,生物体是这种有序结构的实例。
1944年薛定谔(E. Schrodinger)在《生命是什么?》一书中试图用热力学、量子力学和化学理论来解释生命的本质,引进了非周期晶体、负熵等概念。不过,长期以来,大多数科学家都回避生物体有序对热力学的挑战。
但是,科学对人类自身的探索从未停止过,60年代发现混沌现象后,又发现了一大批自然界中自发形成宏观有序的现象——自组织现象,激发了人们探讨这种自发有序现象的不断高涨的热情。
自组织现象俯拾皆是,不胜枚举,远至木星大气层中的涡旋结构,天空中鱼鳞状排列的云街,近至花岗岩中的环状结构,生活中常见的松花蛋中的松花;早至上世纪发现的碘化钾沉淀的Liesegang环状规则分布,近至1900年观察到Benard流体的对流花纹,50年代生化实验中的Belousov-Zhabotinsky化学振荡花纹与化学波,60年代激光器中的自激振荡,等等。都是丰富多彩的自组织现象的典型实例。 Benard在实验室里进行的热对流实验使人们观察到许多令人惊讶的性质,它已成为了解大气和海洋环流以及大陆漂移这样空间大范围运动机理的基础。而就自组织现象来说,又是深入理解非平衡与耗散结构直至湍流形成机制中许多重要概念的基础。
我们已经注意到,自组织现象是体系与外界环境有物质和能量交换的条件下形成的,普里高津把这种在开放和远离平衡条件下,在与外界环境交换物质和能量的过程中通过能量耗散过程和内部非线性动力学机制经过突变来形成和维持的宏观时空有序结构称作“耗散结构”,由于他在这一领域的突出贡献而获得1977年诺贝尔奖。
五、随机非线性微分方程
现在,人们不禁要问,既然在确定性体系中会产生随机现象,为什么不能在确定论的动力学方程中引入随机作用或者补充诸如涨落、噪声等随机因素,使得动力学方程既符合牛顿力学框架的决定论又能满足随机因素的影响而导致非确定性现象的演化过程呢?
其实,在20世纪初,郎之万(P. Langevin)在研究布朗运动时,已经这样作了。当时他在布朗粒子的牛顿运动方程中引入了随机力ξ(t),用来表示一种涨落很快、引起粒子无规则运动的力。这就是第一次在物理学中使用随机微分方程,其后在非平衡统计物理中被广泛推广应用,实际上,郎之万方程是动力系统外在随机性的表现。而混沌现象的发现,说明在某些完全确定论的方程中,并不需要外加任何随机因素(随机初始条件、随机系数、随机外力,等等)即能出现随机演化行为,这就是确定论系统的内禀随机性,也就是引发人们刻意探索的原因所在。
在自然界中,有许多现象并非只有时间渐远时才表现出随机行为,而是本质上既是随机的,又是确定论的。因而描述这一类过程就需要随机微分方程,在非平衡耗散结构的研究中,除了刘维方程加上统计假设的方法外,主要的倒是不需要统计假设,直接从随机微分方程出发,采用半唯象的描述方法。
对于随机现象来说,人们关心的是体系当前时刻的状态与前一时刻状态之间的关系以及它在下一时刻将会处于何种状态。
对于马尔可夫随机过程来说,已知“现在”的条件下,“将来”与“过去”独立无关,了解它的全过程不必求出它的全部有限维分布,而是知道了过程的初始分布后,借助于转移概率来刻画全过程。
当我们研究一个动力系统时,事先并不知道它的概率分布,对于动力系统正在进行的过程,如何去寻求它的潜在的概率分布形式呢?
显然,在过程进行中,在时刻t系统处于j状态的概率由于在单位时间内从i状态过渡到j状态的转移数而增加,同时又随着在单位时间内离开j状态的转移数而减小,由此我们可以得出一个普遍成立的关系:P(j,t)=入率-出率,习馎上称之为主方程,只要根据具体的动力学系统确定了转移概率的形式,就可以求解主方程以便获得有关随机变量的全部信息,进而全面研究相应的动力学系统的演化过程。
六、湍流
自雷诺(O. Reynolds)在1883年进行有关流体流动从层流向湍流发展的实验研究到现在整整一个世纪过去了。在此期间,湍流这一难题曾吸引和激励着从物理学、力学、电子学、大气科学到工程领域的几代科学家致力于探索它。100多年来,由于科学技术的进步,探测方法与技术的改进和新的测量仪器的出现,尤其是计算机科学的迅速发展,在湍流研究领域也获得了可喜的进展。
40年代,朗道(L. Landau)和霍普夫(E. Hopf)分别提出的湍流机制曾为许多科学家所接受,只是到了激光多普勒(Doppler)测量技术成功地测量了湍流发生过程中的频率之后,才确认湍流并不遵从Landau-Hopf理论。由此,湍流研究进入一个新的阶段。人们相继提出了许多新的湍流形成机制,形成了“条条道路通湍流”的局面,混沌现象的研究在科学概念上取得了重大突破,确定性过程与随机过程之间的对立已开始消睁,重正化群方法在相变研究中取得的成功,非线性动力学的迅速发展,协同学、耗散结构和突变理论在科学方法论方面的变革,已从不同的方面为湍流研究取得突破奠定了基础。
其实,湍流并不是只有在科学实验里才能观察和触及到的现象,在人类日常活动中,飞机的起飞降落,船舶在激流险滩中的穿行,石油在管道中的流动,河流的污染,大气和海洋的异常变化,漂移的大陆,袅袅的炊烟,渲泻的瀑布到处都会看到那变幻无常的紊乱的急流和翻滚的波浪,跟着而来的便是吸引着多少探索者欲解其谜的湍流,它既是造成飞机和船舶颠簸航行。
出现事故的原因,又是热在空气中迅速传播开来的动力。当今,对于湍流的了解,几乎仍然是凭经验的,在一个世纪里,只有为数极少的几种湍流预测是从理论上推导出来的,流体力学家把湍流定义为一个连续的不规则流或者一个连续不稳定状态。例如,在紊乱的空气或河流里,流体任一点的运动速度和方向,是不断地和不规则地变化着,而流体却沿着固定的方向继续流动,湍流在平稳的层流中的发展演化是一个连续的过程:起初一个或几个不稳定会激起湍流,它继续增强直到更高程度的不稳定,最后完全发展成湍流——发达湍流。
理论的研究和实验的观测都是以Navier-Stokes流体动力学方程为基础的,它是在连续介质假定下用统计平均的方法建立的流体质点运动方程,也就是牛顿第二定律在流体力学中的应用。造成流体动力学复杂性和多样性的原因是N-S方程中的非线性因素,就是说,流体速度的变化取决于速度本身的平方,同时也取决于压力、动力学粘度或内摩擦,甚至包括边界条件,即使在最简单的湍流中,这种非线性也是引起运动模式在时间和空间两方面复杂性的原因,使方程稳定解失稳。
计算方法与功能强大的计算技术的迅速发展,使湍流的数值模拟和实验观测都在更加广阔的范围内顺利开展起来,发现了一批新的现象,世界许多重要的实验室又重新开始了湍流的实验研究。
当今在湍流研究中,更多地是强调湍流的机理,并不急于涉及全湍流的中心问题,而是着重建立能够进行以简单机理研究为主的模型,这种由简到繁的研究路线是为了通过更多的更深入的了解湍流机理来改善统计理论。可以预计,剪切流向湍流的过渡;由热不稳定性引起的向湍流过渡;在简单机械与电气系统中的紊乱特性等三方面可能是今后湍流研究中的重点。
湍流是自然界中复杂现象的集中体现,描述流体动力学的方程既包含了无穷维的耗散项,又包含了大中小许多不同尺度的运动,也就是说湍流在空间和时间两方面都表现出随机性,在混沌现象的研究中,人们提出了许多通向湍流的道路。例如:
1. Landau-Hopf道路,2. Ruelle-Takens道路,3. 倍周期分叉道路,4. 阵发混沌道路;Spatschek还提出,朗缪(Langmuir)孤波随时间演化将导致一个不可积的非线性薛定谔方程,进行数值模拟,可以观察到一条新的通向湍流的道路,即:孤波→坍塌→湍流。
由混沌现象引发的对复杂性的研究已在许多不同的学科领域迅速开展起来,等离子和磁约束等离子体中的非线性、声学湍流、化学湍流、光学湍流、固体混沌现象、生物混沌等等现象、相继被发现和开展了相应的研究。其中特别值得注意的是,大气湍流的研究进展,大气是进行湍流研究的天然实验室,可以在各种不同的沢度上进行观测实验,从而为湍流的理论研究提供了优越的条件,在大气湍流研究中取得的结果极大地推动了湍流理论的深入发展。人们还建议用螺度(helioity)h=v. rotv来描述湍流的演化过程,提出了软湍流与硬湍流的概念,发展了湍流的多标度分维结构模型与子波分析法,试图建立普适的混沌理论。其次,人们早已熟悉的单极直流发电机的电学方程类似于Lorenz系统,由于单极直流发电机结构非常简单,控制参数改变比较容易,因此是研究湍流的最方便的模型之一。
正当人们致力于湍流问题的解析研究时,曼德勃洛(Mandelbrot)已开始致力于湍流几何学的研究,用分形几何学甚至拓扑学来研究湍流主要是通过分形与分维的概念量度湍流的复杂程度和图像,进一步揭示结构与功能的关系。
大自然无私地把湍流呈现在科学面前,它的千姿百态,瞬息万变和神秘莫测,由型、线、体编织而成的朦胧奇妙的图像,吸引并激励着几代科学家的努力,已经走过了100多年艰苦而漫长的探索之路。混沌的出现,极大地鼓舞着人们献身于这一事业,科学将毫不犹豫和迟疑地迎接对人类智慧的这一挑战,迎接即将到来的重大突破。
(待续)