今天我想同各位谈一个问题，这个问题虽然我本人没有从事研究，但却十分神往。从古至今，许多数学家也为之着迷——这就是素数分布问题。

你们一定都知道素数是什么，它是大于1而又只能被1整除的自然数。至少数论学家们是这样定义的。不过有时别的数学家也采用另外的定义，例如，函数论学家说素数是解析函数

不过我还是希望大家采用我说的第一个定义。

关于素数分布有两件事，我希望它们能使你深为信服，以致使你铭记不忘。第一件事是说，尽管它们的定义很简单，尽管它们的作用只不过是构成自然数的建筑材料，可是素数乃是数学家所研究的对象中最任意和最不易处理的：它们在自然数中就像野草一样乱长，看上去除了服从随机的规律之外不服从别的规律，没有人能预报下一个素数会从哪儿冒出来。另一件事更加令人惊奇，说起来正好相反：素数呈现出美妙的规则性，存在一些控制着它们变化情况的规律，它们服从这些规律几乎就像军人服从命令一样准确。

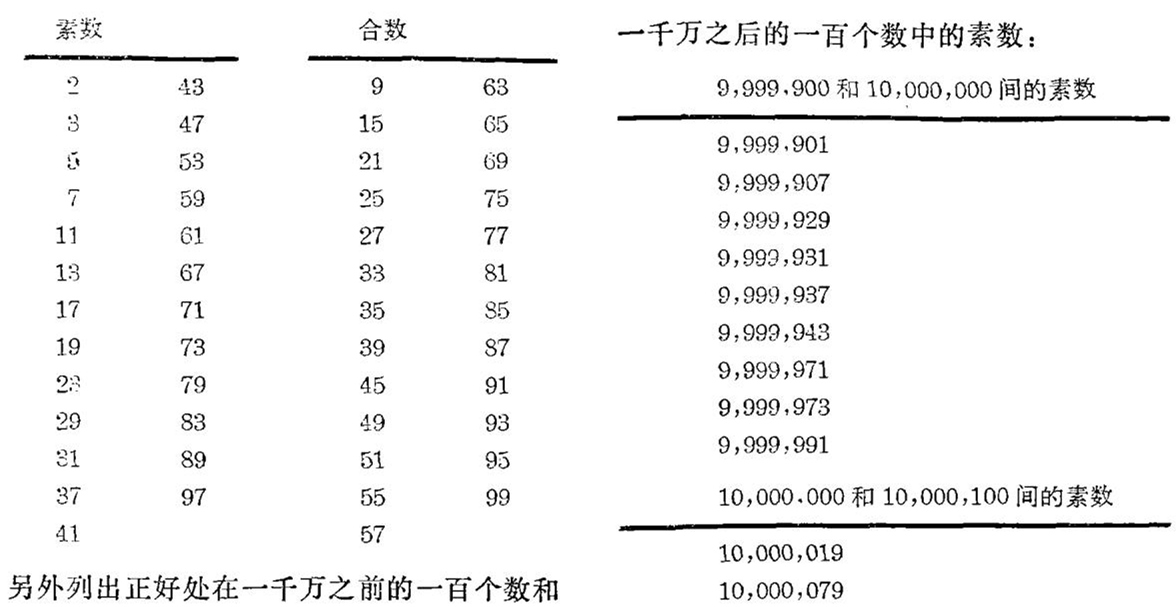
为了说明第一点，我先给大家看一张100以内的素数与合数的表（除2以外，表中仅列奇数）。

我想大家一定同意，没有任何明显理由说明为什么这个数是素数而那个数不是素数。相反，看一看这些数，人们会感到是面对着造物的莫测高深的秘密。即使是数学家们也还没有洞察素数的奥妙，这或许可以从他们热心于寻找越来越大的素数完全得到说明。对于那些有规则地增长的数，例如平方数，2的幂等等，没有人会去操心写出一个比以前已知的更大的数。但对于素数，人们在这方面费了不少心血。例如，1876年Lucas证明2¹²⁷-1是素数，这个纪录保持了七十五年。如果我们看一看2¹²⁷-1= 170141183460469231731687303715884105727那么七十五年没有人突破这项纪录这件事也许就不足为奇了。

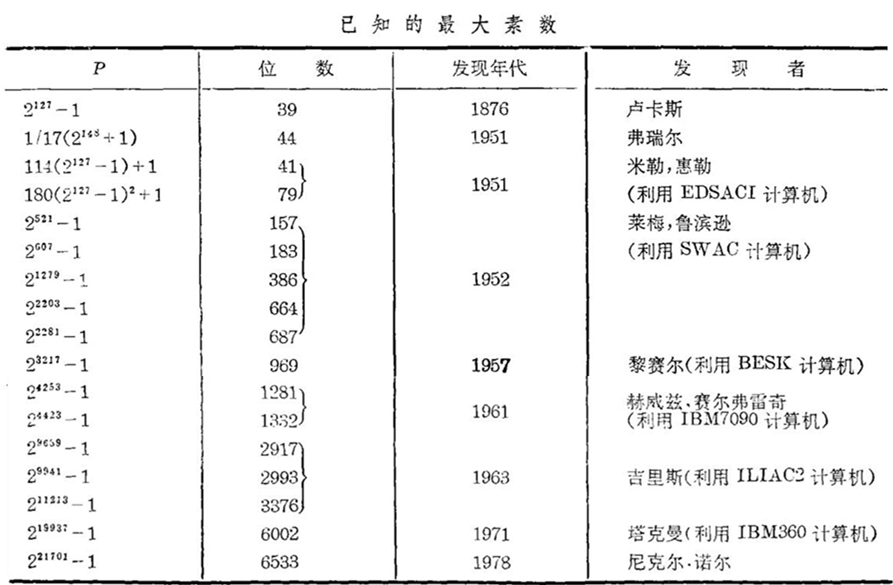
直到1951年，随着电子计算机的出现，才发现了更大的素数。下面附上一张表，你们可以看到历届冠军的纪录^③。目前的最高纪录是6002位的素数2¹⁹⁹³⁷-1（这里我就不细写了）*；如果你们不相信我说的话，可以去查Guinness的书中的有关记载。

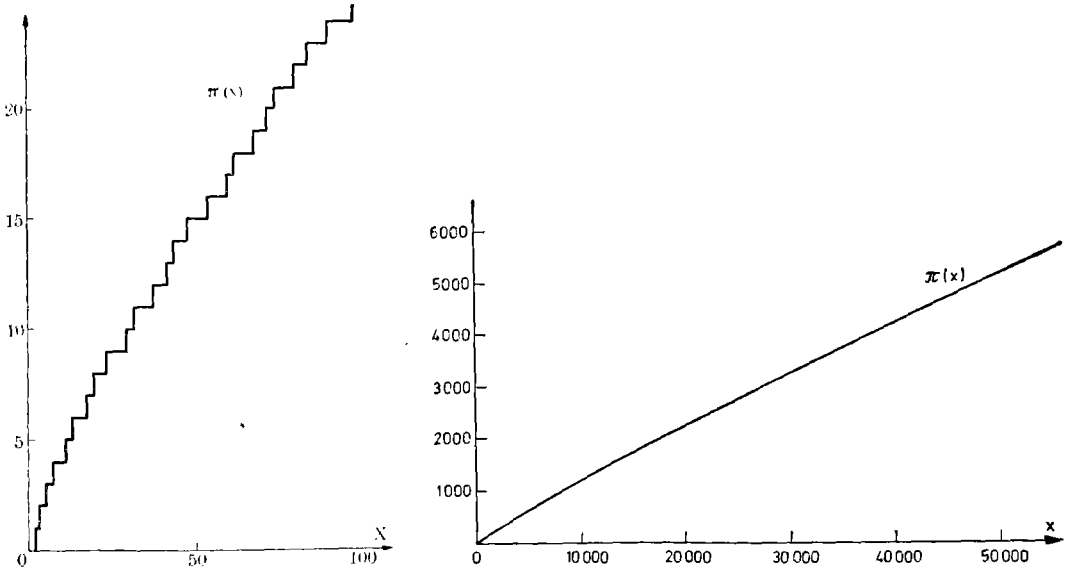
然而更有趣的是素数所遵循的规律的问题。我已经给你们看过了一百以内的素数表，下面用图像来表明同样的事实。记作π(x)的函数（从现在起我们将不断地提到它）表示不超过x的素数的个数；这样，π(x)开始是0，每遇到一个素数如2，3，5等等就增加1。在这张图中我们已能看出，除去小的摆动之外，π(x)一般说来很有规律地上升。

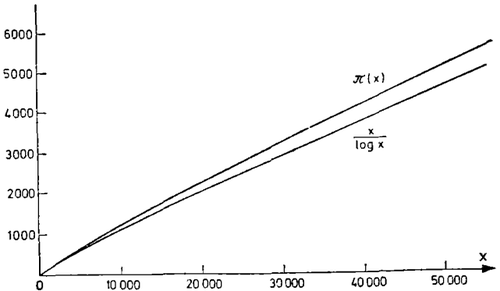
而且如果把x的取值范围从一百扩大到五万，这种规律性就变得惊人地明显，这时图像看上去是这样的：对我来说，这条曲线上升得如此平滑是数学中最令人惊讶的事实之一。

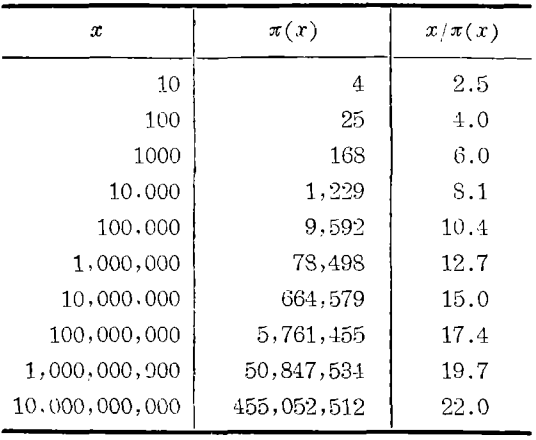
只要自然界呈现一种现象，总会出来一些科学家去寻求解释。在素数中所显示出来的规律性也不例外。找出一个很好地描述素数增长的经验公式并不困难。一百以内有二十五个素数，也就是说有四分之一的数是素数，一千以内有一百二十八个，即大约六分之一的数是素数，一万以内有一千二百二十九个，即约八分之一的数是素数。如果我们扩充这张表，计算素数和自然数的比值到十万，一百万等等，我们就得出下面这张表。（此处列出的π(x)的看去平常的数值。代表着几千小时的枯燥计算）

由此我们可以看出，当x从10的某一个方幂到下一个方幂变化时，x对π(x)的比值总是接近于这个幂次的2.3倍。数学家们立即认出2.3是10的对数（当然以e为底）。这使我们猜测

π(x) ~ x/logx

此处符号 ~ 表示当x趋于无穷时π(x)/(x/logx)趋于1。这个关系（直到1896年还没有人能证明）称为素数定理。最伟大的数学家高斯（Gauss）十五岁那年，在研究一本有关对数的书——这是他前一年得到的礼物——中的素数表时，发现了这个事实。高斯毕生都对素数分布问题非常感兴趣，并做过大量的计算。在给Enke^④的一封信中，他曾说过他是如何“随时随地利用空闲的十多分钟计算连续一千个数中的素数”（即一千个数的区间）。最后他列出了三百万（！）以内的素数表，并把它们的分布情况与他猜测的公式做了比较。

素数定理表明π(x) ~ x/logx渐近地——即以0%的相对误差——等于x/logx。但是如果我们比较一下函数x/logx和π(x)的图像，就会看到，虽然x/logx定性地反映了π(x)的变化趋势，不过要用来解释π(x)的平滑性，毕竟与π(x)拟合得不十分好。

所以当然需要更好一些的近似公式。如我们再看一下π(x)与x的比率表，就会发现这比率几乎精确的等于logx-1。根据更细致的计算和π(x)的更详尽的数据，Legendre^⑤在1808年发现，如果从logx中减去1.08366而不是减去1，就得出一个特别好的近似公式

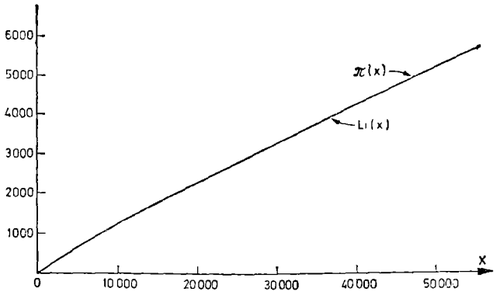
给出。现在我们如把Li(x)和π(x)的图像作一比较，可以看出在图像的允许误差内二者精确地相合。

没有必要再去画勒让特公式的图像了，因为在图像的范围内，它是π(x)的一个更好的近似。

我还想谈一谈另一个更准确的近似公式。Riemann对素数的研究表明，如果不只计算素数，还计算它们的乘幂，把素数的平方算作半个素数，素数的立方算作三分之一个素数等等，则一个大数x是素数的概率将更接近于1/logx这样就引出如下的近似公式

对于这一点我应该强调一下，高斯和勒让特的π(x)近似公式纯粹是经验地得出来的。即使是黎曼，尽管他经过理论考虑得出他的函数及R(x)，但他也从未证明素数定理。这个证明首先由Hadamard和de la Vallée Poussin互相独立地完成。他们的证明都基于黎曼的工作。

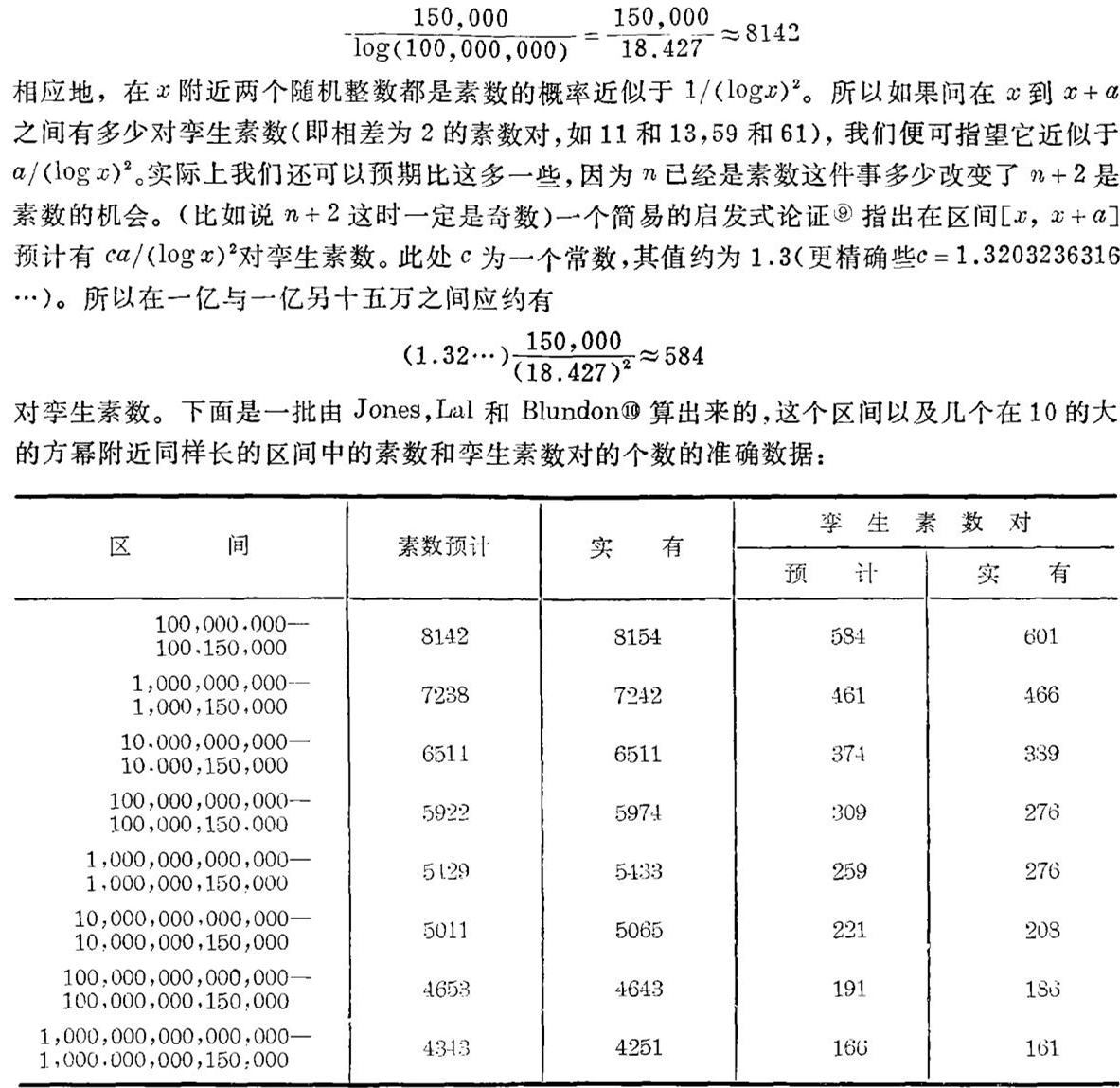
此刻正在讨论能不能预报素数这个问题的时候，我想给出一些更带数值性的例子。如前所述，数量级为x的数是素数的概率大致是1/Iogx；也就是说，至少对于一个长度与x相比是很小，但本身又长得足以具有统计意义的区间来说，如果它位于x附近，长度是a，则其中素数的个数应当近似于a/logx。例如，我们可以指望在一亿与一亿零十五万之间找出大约8142个素数，因为

你们可以看出，这些数据和理论的符合程度是极好的。其中孪生素数的情况特别值得惊奇，因为这种数对是否有无穷多迄今尚未证明，更谈不上它们是否依照所猜想的规律来分布了。

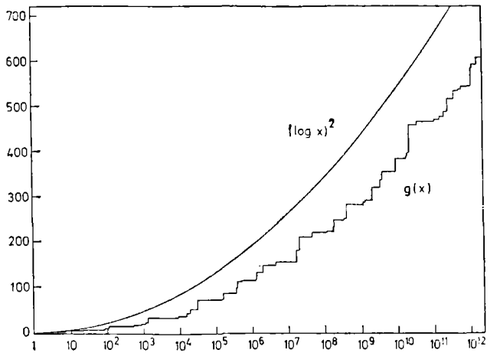
关于预报素数的可能性，我想再做一最后的说明，那就是素数之间的间隔问题。看一下素数表，有时会发现一些很大的间隔，例如在113和127之间没有任何素数。设g(x)表示不超过x的最大无素数区间或“空隙”。比如200以内的最大空隙就是刚才说过的113到127，所以g(200)=14。当然g(x)是十分无规则地增加的，但一个启发式推理提示这样的渐近公式^?

g(x) ~ (Iogx)²

从下图中你们能看出，即便是这个极不规律的函数g(x)也保持着预期的变化趋势。

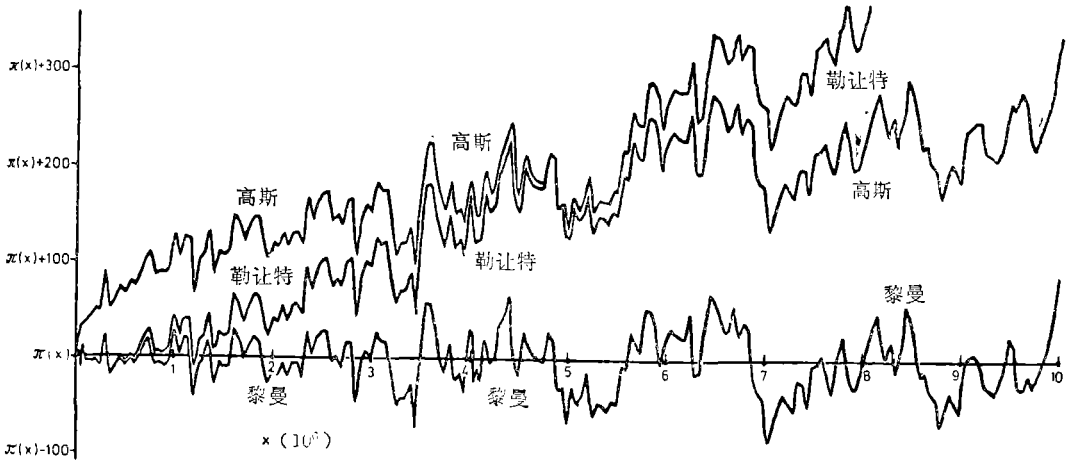
直到现在，我对于证实关于素数是有规律的这一方面说得较多，而没有足够地讨论它们无规律的一面。同时，我只提到了前几千个素数，而没有像我的讲演题目所许诺的，给大家讲解前五千万个素数。下面是一张在一千万以内比较π(x)和勒让特、高斯和黎曼近似公式的图。^?因为这四个函数非常接近，画出图时肉眼无法区分（正如我们在不超过五万的那张图里见到的那样）所以我们就只画出它们的差：

我认为这张图告诉我们，一个有志于研究数论的人会遇到什么问题。

正如你们能看到的，对于小的x（直到一百万左右）勒让特公式x/(logx-1.08366)明显地优于高斯公式Li(x)，但超过五百万以后，Li(x)就好些，可以证明当x再增加时，Li(x)总是较优。

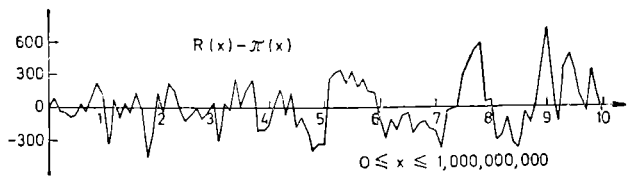
但是一千万以内只有约六十万个素数，要想让诸位见到我许诺的前五千万个素数，就不是走到一千万，而要一直走到十亿开外（美国记法是10⁹）。在这个范围内R(x)-π(x)的图像看上去是这样的：^?

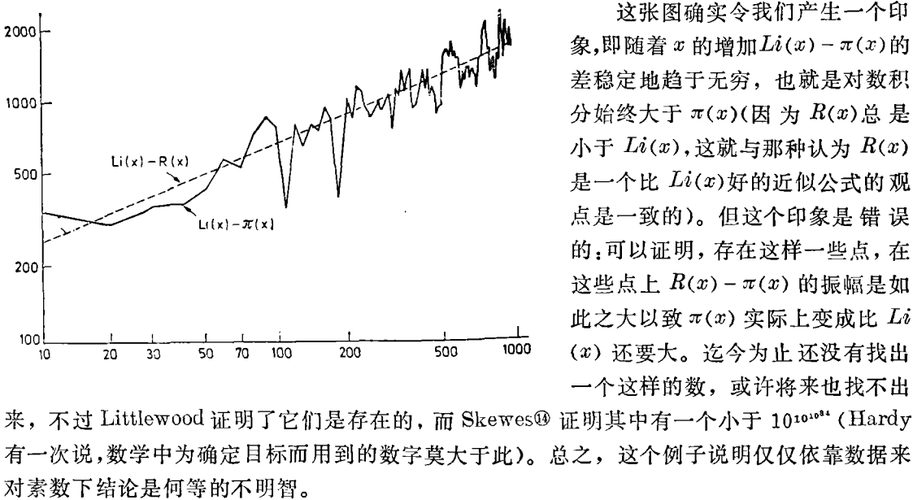
联系这些数据我就能谈谈另一个关于素数个数π(x)的事实。在到一千万为止的那张图中，高斯近似公式的值总比π(x)大。而且在下图中你们可以看到，直到十亿仍是如此（图中上述数据是用对数坐标画的）。

在讲演的最后部分，我想说一些有关π(x)的理论结果，以便大家听完讲演后不要感到只看了一场实验数学。缺乏数论知识的人一定会认为一个数成为素数是太偶然了，以至关于它我们证明不出什么东西。这一点在两千二百年前就被Euclid驳倒了。他曾证明有无穷多个素数存在。他的证明可以用一句话来概括：如果只存在有限个素数，那么把它们乘起来再加1，这样得出的数不能被任何素数整除，这是不可能的。到18世纪Euler进一步证明，素数的倒数之和发散，也就是这个和数最终将超过任何预先给定的数。他的证明也很简单，利用了函数

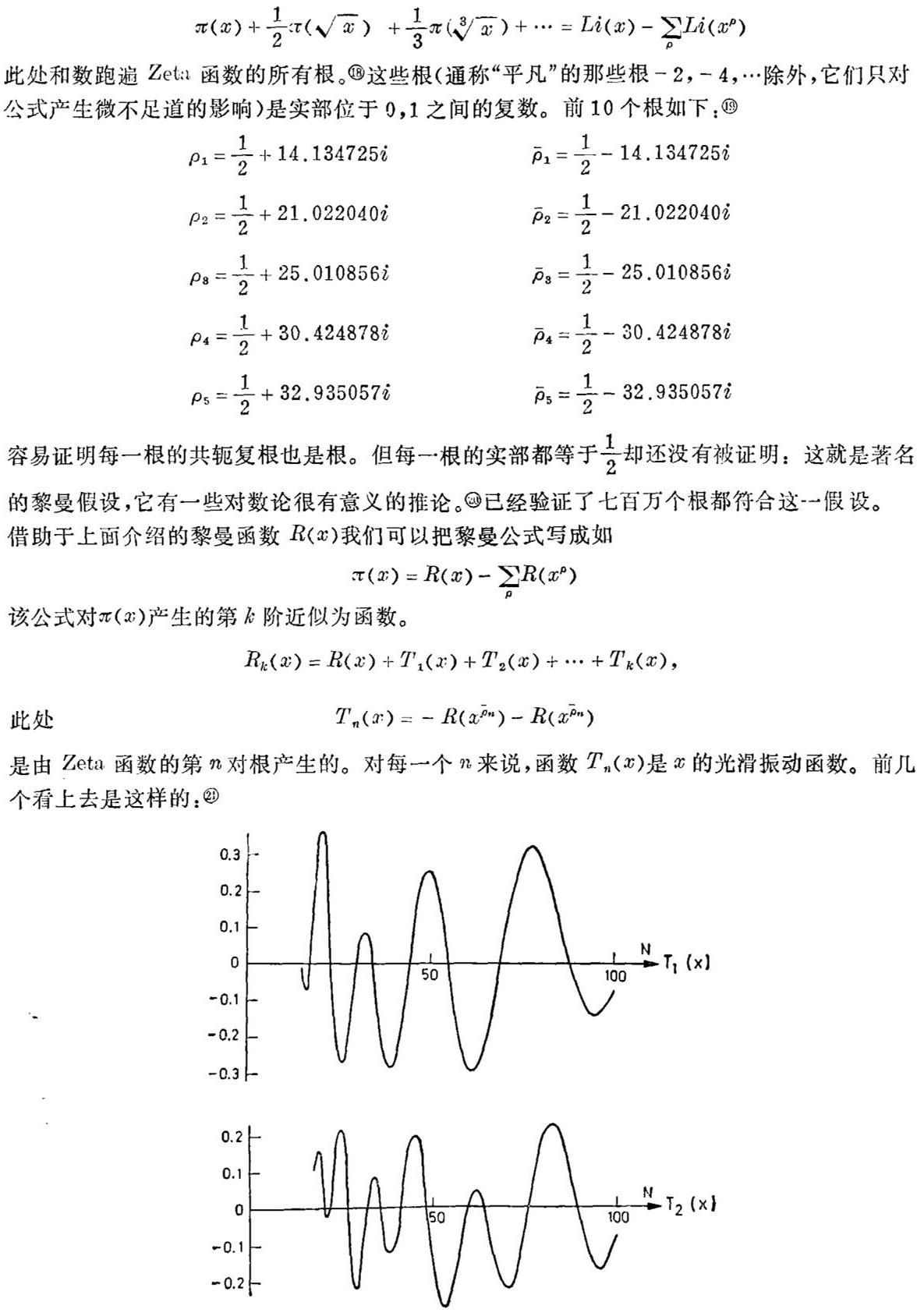
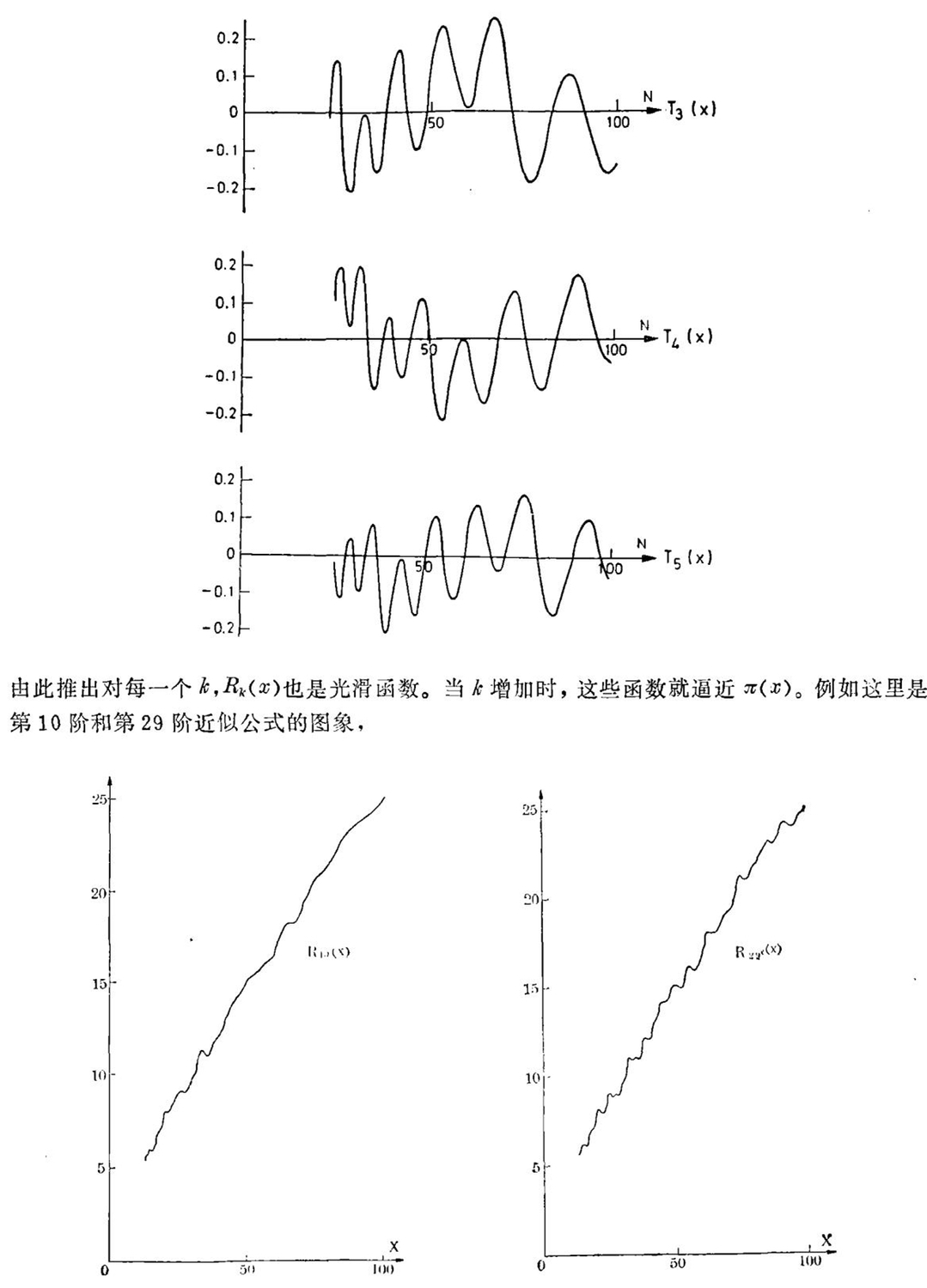
作为结束，我想对黎曼的工作再谈几句。虽然黎曼没有证明素数定理，但他做出的东西不管怎么说都是很了不起的——他发现了π(x)的准确公式。这个公式的形式为

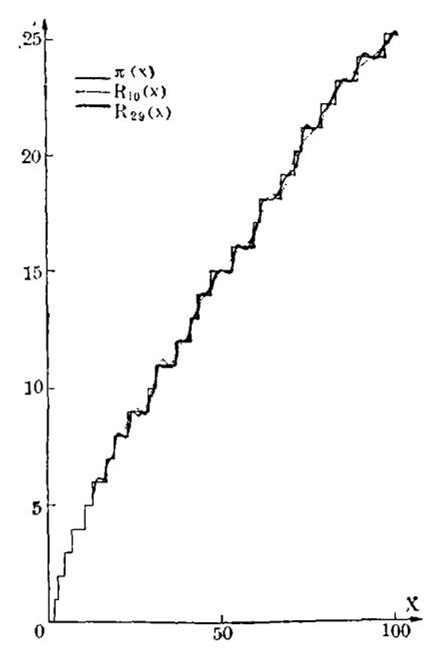
同时，若把这些曲线和100以内的π(x)的图像相比，就得出下面的图：

通过我给你们看过的这些图，我希望能使你们对于素数的无比美妙和它留给我们的无限惊奇之感有了一定的印象。

[译自The New Mathematical Intelligencer1977年。孙捷 译]