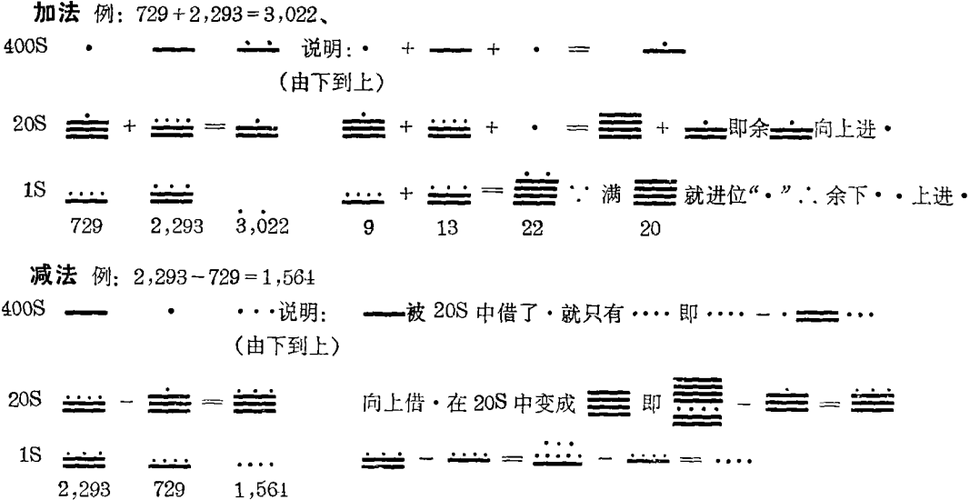
玛雅人只用两个符号“ · ”和“——”组成了所有的数字,并利用简单的运算顺序来进行多种复杂的计算。
远在欧洲人到达新大陆前,墨西哥和中美洲的玛雅人已创造了各种数学符号来进行算术运算,比罗马制算法早了一千多年。玛雅人用“ · ”和“——”组成了各个数字,并用它们进行加法和减法的运算。
玛雅人的“ · ”表示一个单位,“——”表示五个单位。由于宗教和生活上的原因,他们很巧妙地把“ · ”排在“——”上,用这两种符号组成了1 ~ 19各个数字,如下:
阿拉伯数制以十进位为基础,由右到左,个位、十位、百位……玛雅人的数制是以20进位为基础,即个位、20位、400位、8000位它的单位制可能是根据人的手指和脚趾的总和;不过,适用于历法计算可能是重要的原因。因为低地玛雅人的历法是以18而不是以20进位的,他的1就表示1天、20天粗略为一个月、360天(20×18)估算为1年,7200天为20年,而144000天为400年等。
他们组成数字的办法,把每个单位的符号由下向上地堆积起来,例如阿拉伯数的729,由1个400,16个20,9个1组成(20进位表示为1.16.9)。
因此,玛雅人的加减法要比阿拉伯数的加减法简单得多。
玛雅人能熟练地运用这种加法和减法的过程,在一连续的运算中可加进或减去一系列的数。墨西哥犹哥泰地区(Yucatán)的第一主教Diego de Landa说,玛雅人“在地上或在平面上进行这些运算,使人想到这是一种动态的运算,而不是静态的运算”(de Landa 1566)。J. EricS. Thomson推测说,他们把玉米、豆子或卵石作筹码,表示“ · ”用豆荚表示“——”的符号(Thompson 1941)。利用豆子、卵石和豆荚可作迅速地运算,成了现代算盘的雏形。
乘法
到现在还没发现玛雅人使用他们的符号来进行乘法和除法的运算;Thompson(1941)认为,“从德累斯顿的古代圣经中,发现有大量的证据表明玛雅人的算术没有包括乘法和除法,但利用加法和减法也能达到同样的结果”。而Satterthwaitet(1947)则认为,玛雅人不会做乘法和除法,但他没有提出这方面有力的证据。事实上玛雅人早就有了乘法和除法及它们运算上的语言(Solis-Alcalá 1949)。现有的对玛雅人的这种看法是受了现在出版的各种数学书籍的影响。
德累斯顿的这本圣经是十二世纪Yucatan的抄本,当中记载着玛雅人的算术。圣经第32页(见封四左图),示玛雅人的加法表。左图中间一张图的下半部可以找出78的倍数。260圣日的三个循环,历法上为780天。780天分10段,每段为78天。表上可看到780和260的另一些倍数。当一个数位上是空白时,就用壳状的符号填上(封四右图)。该书第44页的上部分,示364和91的倍数。这本古老圣经的插图中,还表示了金星运行的周期(Lounsbnry 1976;Aveni 1979),可是Thompson(1972)认为,从这表上可看出玛雅人对直接乘法的无知。
由于自然观念的影响,我们的知识水平受到限制。现在我们了解的玛雅人的算术大部从他们刻在石碑上的历法,宗教的教规上得来的,正如我们可以从刻在墓碑上的(碑文)阿拉伯数中学到一些算术一样,碑文中的死期减去生期就可算出年龄的大小。现在虽然还没有掌握玛雅人乘法和除法的足够证据,但Satterthwaite认为不能武断地否认这两种运算法则在玛雅人中的存在。我们只能说对这个问题还没有一个明确的答复。
玛雅人的算法与日历中规定的计算程序是差不多的。Landa(1566)主教对此作了明确的解释,“在当时的可可交易中,玛雅人采用了这种计算法则。”这位主教与其他的学者一样,他们的研究是为了找出玛雅人算术中更有趣的事情。
现在Satterthwaite提出了对玛雅人的乘法及除法的见解。他认为玛雅人这种算法的程序是非常麻烦(你做过罗马数字的乘法吗?),还包括许多要记牢的乘法法则。1961年George I.Sánehez私人出版了一本有价值的小册子,它介绍了玛雅人数学的符号——进位制和分数。几年以后,我们根据Sanchez的著作又发现了玛雅人符号的意义和简化了数学运算的法则。
现在,我们利用现时的数学规则来解释和推导出玛雅人乘除法的程序。
玛雅人表示数的符号只有“ · ”和“——”,有三条法则可表示它们间的乘法关系,把它与阿拉伯数对应起来,见下表。
以上是谈了乘法的程序,实际计算时要比这快得多,因为玛雅人用卵石和豆荚当作算盘依照这个计算次序做乘法的。
上例中,乘数和被乘数是在1S中的乘法。如果乘数和被乘数超过第一位,就要决定各个单个乘积大小的次序和单个乘积总和的次序,也有它的法则。
n和m表示位的次序,n和m为1就是1S,为2就是20S。这条规定适用在各个位上的“ · ”或“——”。
1, ·(在n位上)× ·(在n位上)= · (乘积在n+m-1位上)
2,——(在n位上)× ·(在m位上)=——(乘积在n+m-1位上)
3,——(在n位上)× ——(在m位上)= ·(在n+m位上)+——(在n+m-1位上)
利用以上举的做乘法的次序和定位法可做任何乘法,有下列为证。
除法
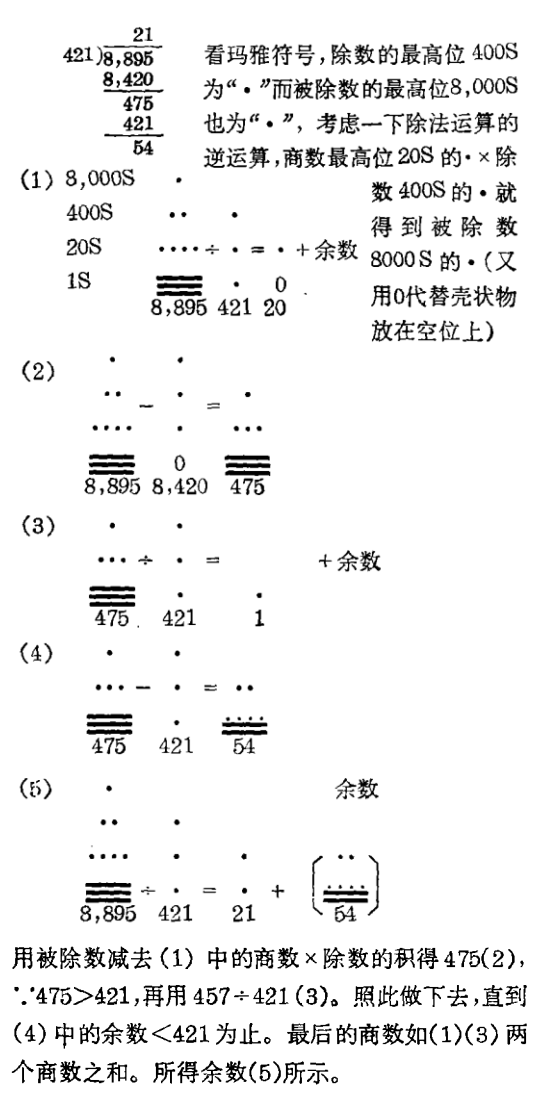
玛雅人的除法与阿拉伯数字除法的次序是差不多的,是乘法的逆运算。用除数的最高位的数去除被除数的最高位的数……,结果就是商的最高位数附加上一个余数。如果这个余数大于除数,再要用余数去除以除数,直到最后的余数小于除数为止。以8,895+421为例。
必先做阿拉伯的除法,排出直式。
以上的图是为了演示玛雅人除法的顺序。玛雅人虽然用豆荚和卵石来运算,但他们运算的程序却是非常先进的。运算时的商数是从高位做到低位,而从原来的被除数中减去商数x除数的积,就得到余数,如果余数>除数,那就要再做下去。在这个解法中,中间的运算步骤就不必写出来。
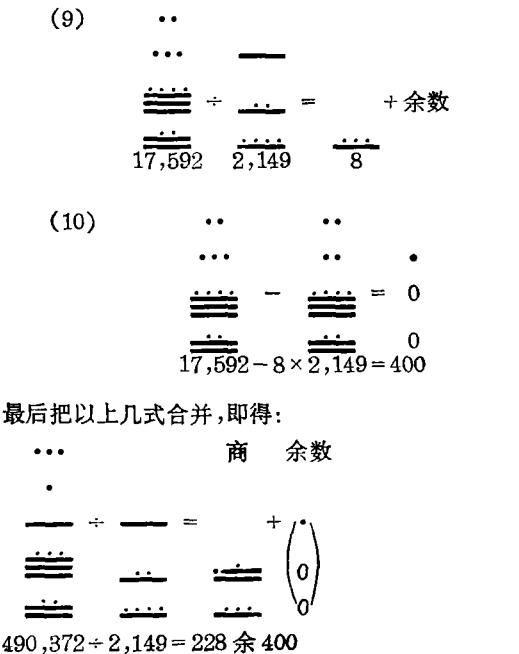
上例中商数的各位上只有 · ,下面再举复杂的例子,商数的各位上既有又有“ · ”“——”,从商数的高位做到低位、分解成单一的步骤,直到余数小于除数为止。下面以490,372+2,149为例。
像十进制的除法一样,我们立刻所指出商数的最高位在哪儿。
用原来的被除数减去472,780得的差(余数)大于除数2,149,(8)用同样的方法完成17,592-2,149=8+余数(9)
虽然做这个除法时用了长长的六步,可它同时用了两套路子来完成。一套是商数的变化,另一套是被除数变换成余数。我们可以利用玛雅人的这一套快捷而又简便合理的办法来启发初学者学算术的思路。
玛雅历法
修正的数学
玛雅人只用了两种符号,再加上那朴素而简易的方法,组成了他那特有的算术运算法。两种符号的相互交换,成为一种机械的动作,它使必须记忆阿拉伯数学的乘法表成为多余的。
阿拉伯数字的运算和玛雅人的运算还有根本不同的地方,阿拉伯数学的运算是在纸上进行,而玛雅人的加减运算可用筹码进行,后者不是一种死板的过程。
在用筹码运算熟练后,中间的过程就不会考虑了。在历法与商业交易中,玛雅人用了加法和减法,而现在还在怀疑古代的玛雅人有否必要用除法,但这并不是最后的定论。因为学者们已经证明了玛雅人的数学符号有做乘法、除法运算的能力。可以肯定,我们一定能发现玛雅人的这两种运算步骤。毫无疑问,玛雅人的运算还没被我们完全揭示出来。例如Sánchez在1961年就提出,阿拉伯数字中的带有小数的数字也可用玛雅人的法则来表示。
虽然玛雅人的数学法则还没发展到完美的地步,可是已给了我们很大的启发。
〔译自American Scientist,1980年5 ~ 7月〕