核子结构

发布时间：84年02月28日

Gerald E. Brown① Mannque Rho① 编译烨苓

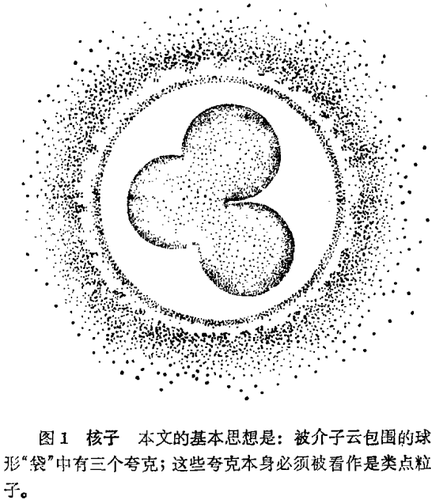
核子或许由形如口袋的夸克小核以及围绕并挤压此夸克袋的介子云构成。

早一时期，我们已经知道核子必定有一个非无限小的尺寸。五十年代，随着量子电动力学的定量计算技巧的发展，出现许多描绘核子大小的尝试，但都没有成功。夸克物理的问世以及电子受核子的高能深度非弹性散射的实验验证，说明在核子的中央核心处存在三个客体，它们以高能态运动着，似乎是自由、并且没有质量的，从而促使建立起一种对核子结构的崭新描述体系。自从洛仑兹对电子理论进行研究以来，我们已经试图给出基本粒子的有限尺寸，以使其自能不致发散。现在，我们已经构造了“口袋”（或称作“汽泡”），以容纳夸克存在，并相信真空在袋上产生压力；而这种真空压力阻止口袋膨胀。本论题指明（如图1所示），可以把核子认作这样一种被介子云包围的气泡中的三个有色夸克体系。

目前的看法可简述为如下几点：

（1）核子的受激谱比三核子体系的受激谱简单得多，因为夸克不能彼此离得无限远，核子没有连续谱。

（2）分裂核子态的剩余力与原子物理中的情况极为相似，只要以色耦合常数α₃代替原先的精细结构常数α即可。

（3）夸克图像，特别是“渐近自由”这个概念，能够提供一种处理核子 - 核子短程力的机制。

本文将描述关于核子结构以及核子在原子核中行为的现代图像的复杂状况。我们将会明白，核子的“袋”模型是一种吸引作用理论，它使人们借以进行许多计算；在这种模型里，夸克被规定为受到禁闭。并且还将看到，对称性条件和守恒定律如何暗示π介子云包围了禁闭区域，而π介子云如何使核子的夸克核心的大小保持为大约0.5费米。核子内存在夸克核心这一点，要求我们修正关于核子短程作用的玻色子交换的传统模型。

核子有多大？

可以认为，核子大小的最好标志，或许是描绘核子内电荷空间分布的电形状因子，它通过电子弹性散射予以确定。借助于对电形状因子的研究，我们已经精确地确定了原子和原子核的大小。然而，我们将要描绘目前流行的图像之一，乃指核子包含两个区域：一个是核心区域，其中质量接近零值的夸克几乎自由地运动，夸克之间只有弱相互作用——这就是所谓渐近自由的情况；另一个是较大的外部区域，其间存在π介子和其他介子，我们称之为介子云。

如果在关于强相互作用的现代理论——量子色动力学（QCD）中忽略夸克质量，那么存在一种由夸克的运动方程引出夸克螺旋性守恒这个事实所产生的协变性。这就是SU（2）× SU（2）手征协变性。倘若真空服从这种对称性，那么相互作用便不能破坏其手征协变性，而且或许会有自然界里经常观察得到的、普通的多极结构，此时上夸克（u夸克）和下夸克（d夸克）就没有质量。这通常称作威格纳 - 韦尔（Wigner-Weyl）模型，或简称威格纳模型。

现在假定真空对于夸克 - 反夸克对凝聚是不稳定的。凝聚对必须像真空一样，没有角动量和线动量，而且其螺旋性必然不能守恒。当凝聚发生时，真空便选出一个优越的方向，夸克变成有质量的东西。而SU（2）× SU（2）对称性就破缺，降为同位旋群SU（2），每个破缺的群生成元产生一个被称作戈德斯通玻色子的粒子。当不计及π介子——π⁺，π^-，π⁰——的很小质量时，它们便是戈德斯通玻色子。这种关于对称性破缺的方式被称作南部 - 戈德斯通（Nambu-Goldstone）模型，或简称戈德斯通模型；人们相信该破缺方式在自然界里可以实现。而此手征对称性的破缺又据说是自发产生的。

至少在半经典水准上，自然会假定，核子内部两个区域之间有一个交迭部分；而在这两个区域里手征对称性取不同的形式：内部遵循威格纳模塑，其间受禁闭的夸克几乎没有质量；外部遵循戈德斯通模型，其间有介子存在。虽然我们采用戈德斯通模型进行描述，但并不意味着介子不是由夸克和反夸克组成的。然而，用介子名词讨论夸克 - 反夸克凝聚是方便的，正如许多年来人们谈论有关原子核表面区域的α粒子凝聚的情况一样。只是这儿与原子核图像存两点根本不同：

（1）对于π介子，只有以与核子核心处不同的方式，才能实现其手征对称性。

（2）π介子不能分裂成夸克和反夸克，而α粒子可以分裂成几个核子。

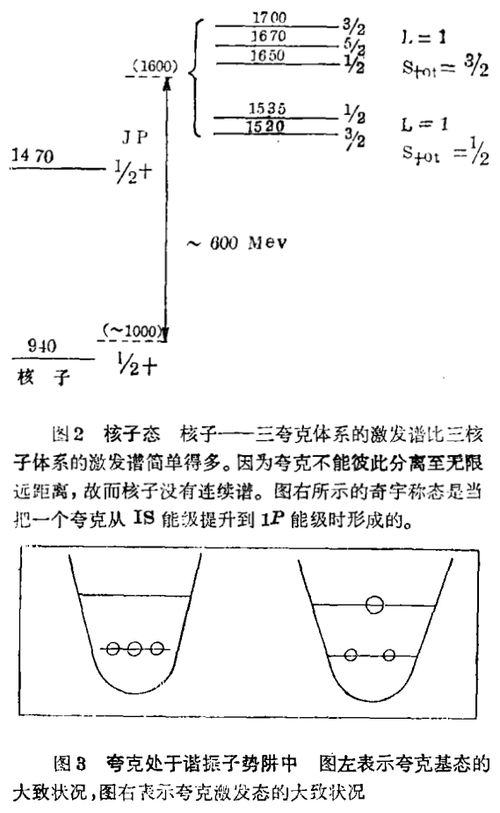
我们不再为描绘核子内两个区域的大致面貌而花费很多笔墨，还是来看看核子的激发谱。对于诸如H³或He³那样的原子核三体体系，一旦核内三核子中的一个具备足够的能量，便形成其激发态，它处于连续谱区之中，所对应的波函数一直延伸到无限远处。而对于三夸克核子体系，其中夸克被禁闭，单个夸克不能运动到离另外两个夸克很远的地方。因此，核子的激发谱相当简单，即如图2所示。该图表明了核子的基态、第一偶宇称激发态[称为罗珀（Roper）共振态] 和几个奇宇称态。至于其他激发态都在1700 MeV以上。

谐振子势 奇宇称激发体系的自由度可以通过很简单的方式理解。正如许多人所想象的那样，夸克处在谐振子势阱中（见图3）。对应于图3右边所画的能级有五个奇宇称激发态：三个夸克的自旋耦合，给出其总自旋为1/2或3/2，然后总自旋角动量再与L=1的轨道角动量耦合，得出下列总角动量：

式中f是r_ij的正值函数，所以当核子处于其夸克的自旋彼此平行的状态时，这种相互作用是斥力，因此，S_总=3/2的态相对于S_总=1/2的态，其能量有所上移；此情况从图2中可见：对应于S_总=3/2的三重态在对应于S_总=1/2的二重态之上。之所以三重态和二重态不自相简并，是因为除了自旋 - 自旋相互作用外，还存在别的作用力。到此我们已经明白，最低的五个奇宇称态，可以用上而列出的J的五个数值标记。

决定，式中m_Q是夸克质量，α是半径参数。问题是：什么是夸克质量m_Q？其答案目前还不明白，可能必须待夸克禁闭问题解决以后才会搞清。然而从对诸如磁矩那样的各种性质的测量结果出发，我们可以认为，夸克的质量似乎大约为核子质量的三分之一。这一点具有一种简洁的、靠不住的直观性：如果三个组元夸克组成一个核子，那么最自然地会假定，要是置结合能于不顾的话，三者质量之和应该等于核子质量。这样一种夸克具有质量的模型称为“组元夸克模型”；可以把它看作是与多体系统中的准粒子图像类似的一种东西。然而m_Q不可能是通常意义下的质量。

由于夸克的质量是核子质量的三分之一，从上面的式子便得出其半径参数α等于0.45费米。而基态的方均半径由下式给定：

<γ²>_核子=3/2α²

但这里包括一部分因伪质心运动产生的影响；若把它除去，则自由度的数目便从3降为2。因此我们把上面的结果乘以2/3，于是得出基态半径α的方均根值：0.45费米。与此类似，对于奇宇称激发态，可得出其方均根半径为0.50费米；该值必定大一些，因为这些激发态处在势阱的较高处。

胶子交换效应

哈佛大学的阿尔瓦罗 · 德 · 罗耀拉（Alvaro De Rujula）、霍华德 · 乔治（Howard Georgi）和谢尔登 · 格拉肖（Sheldon Glashow）的工作阐明了胶子交换的相互作用与原子物理中光子交换的电磁相互作用之间的相似性；这是讨论本课题的良好出发点。我们仅仅考虑夸克和胶子的最低级耦合，因为在近距离上夸克是渐近自由的，其耦合是微弱的。我们来讨论夸克的短程微扰作用。对于最低级近似来说，夸克和胶子之间的耦合由一拉氏量给定；该拉氏量，除了其中跟色自由度有关的那些矩阵而外，与关于光子和电子的耦合的拉氏量非常相似。只要以夸克 - 胶子耦合常数g代替电子电荷量e即可。

图4表明，夸克间的短程相互作用由交换虚光子而产生。这种相互作用恰好具有与两个相对论粒子之间的电磁相互作用相同的形式，但须以-2/3g²代替电荷的平方，其符号表示是正负电荷之间的相互作用。因此，各种效应的符号或许与氢原子中的电磁相互作用的情况类似；虽然其作用强度可能完全不同，因为g²尽管甚小，但比电磁常数e²还是大得多。

式中C把几个常数及径向积分都总括在内。对于三体体系，这个和值早已算得：对核子来说，此值为-6；而对同量异位素来说，此值为+6。Δ(1230)具有能量300 MeV，这比核子的能量大。因此，若把全部能级分裂都归因于一种胶子交换的自旋 - 自旋相互作用，C则为25 MeV。这里，张量相互作用或许没有贡献，因为它是一些球对称空间状态的平均值。而自旋 - 轨道相互作用不出现，因为在这些态中L=0。

研究者们已经把上面这些简单的看法用于描述核子奇宇称激发态的能谱，并取得相当大的成功。正如图2所表明的，对应于S_总为3/2的J=1/2，3/2，5/2的三重态，其能量高于对应于S_总为1/2的J=1/2，3/2的二重态。借助于谐振子波函数，由式2描述的相互作用可以给出这些态的质心分裂数值正好是Δ(1230)- 核子分裂数值的一半。就是说，三重态的能量大约高出二重态150 MeV；这与实际情况符合得很好。

我们还能够搞清介子和奇异重子在某些同类谱线上的一般的能谱特征。微扰处理的胶子交换，给出了一种简单的统一的一级近似图像。

磁矩

最初，人们认为核子的反常磁矩是由介子云产生的；而夸克模型出现以后，则认为所有磁矩都是由夸克提供的。现在有迹象表明，实际情况兼具上述两种图像。

夸克模型因取得如下成就而琴到激励以至得以发展：给出质子磁矩跟中子磁矩之比为-1.5，与实验值-1.46相差无几；关于SU（6）的一篇论文中说明了这一进展情况。但是核子只包含四种夸克（上夸克和下夸克，每类又分为两种自旋方向），因此磁矩计算只涉及SU（4）。

质子有两个上夸克和一个下夸克；中子有一个上夸克和两个下夸克。所以每个核子含有两个相同“气味”的夸克。由于色波函数总的来说是反对称的，故而味波函数必定是对称的。因此，两个同类夸克必然处在同样的自旋态上。那么可以利用矢量加法把两个同类夸克的磁矩与第三个夸克的磁矩相加而得出核子的磁矩：

式中m_A和m_p为Λ粒子和质子的质量。（推广后的图像称作“SU（6）破缺”。该SU（6）破缺模型包含六个客体：带有两种自旋投影的上夸克和下夸克以及具有岗上自旋和向下自旋的奇异夸克。其对称性因奇异夸克的质量不同而破坏。）Λ粒子的同位旋为零，因此，倘若上夸克和下夸克的自旋和同位旋是对称的，那么这两种夸克必然耦合而得出净自旋为零。所以，Λ粒子的磁矩就是其中奇异夸克的磁矩：

μ_Λ=-1/3m_n/m_B=-0.61

对此量进行测定，其结果与预言的数值精确地符合。如此巨大的成就使夸克模型获得进一步前进的动力。

在上述发展之前，对于通过光子与处于核子基态的ρ矢量介子和ω矢量介子的掺和物之耦合而产生质子和中子的反常磁矩这一点来说，矢量（介子）为主模型似乎是相当成功的。矢量为主模型中的主要假定是：ρ介子和ω介子的电生成过程的γ射线耦合与其跟磁矩的耦合相同；也就是说，对于类时动量转移和微小的类空动量转移，其耦合方式是相同的。在此假定之下计算质子和中子的磁矩，所得数值正在最近实验数据给定的误差范围之内。认为矢量为主模型是成功的，这不足为奇！因为矢量介子通过π介子相互作用与核子耦合，这些介子会混合形成介子云。

现在我们有两种图像描述核子磁矩：一种是依据夸克模型；另一种是通过矢量介子的耦合。在如此状况下，若更深入地考虑一下，往往会明白，这两种图像描绘了同一基础性理论的不同方面。SU（6）图像把全部磁矩都归因于核子波函数的三夸克部分。至于矢量为主模型，则把全部磁矩都归因于矢量介子的混合物；而介子是夸克 - 反夸克对。

目前的研究表明，核子磁矩是由组元夸克和介子云几乎以均等的比例产生的。假定50%的核子磁矩由介子云提供，那么通过一定的计算可得出与实验值符合得很好的结果。待等实验精度进一步提高以后，我们对介子云贡献和夸克贡献的精确分配比例数值将会改变；但要说可比拟的影响由这两种实体（介子云和夸克）的运动引起，总是适当的。

MIT袋模型

在确证核子是由夸克组成时，以为夸克的行为似乎是自由，而且没有质量的。实际上，那正是高能深度非弹性散射实验的显著特征。那么，已经采用已久的夸克质量m_Q又是如何发源的呢？当然，我们的讨论是在低能范围进行的。按照动量大小的不同，其耦合方式亦会改变，因为当动量变小时，相互作用变强，阿以便可能出现关于夸克获得质量的机制。然而，MIT袋^②颇引人注目，其中上夸克和下夸克的质量几乎都为零（略去了很小的上下“流夸克”质量，大约为几个MeV）。从那几种基本的零质量夸克出发，就更容易实现其手征对称性。

在MIT模型中，夸克被规定为受到禁闭——对于夸克波函数，在半径为R的球面上，即所谓“袋”的边缘处限以一边界条件。利用这个边界条件，可以证明：在r=R处矢量流的法向分量为零。因此，没有粒子可以从袋中逃逸出去。给定了MIT边界条件，便可解出夸克的波函数；在袋内，该波函数服从零质量费米子的狄拉克方程。

物理真空是规范场的一种复杂到令人望而生畏的带色的“实心细面条”，并带有一种夸克对凝聚的“调味品”。为了允许有色夸克局部存在，必须构造一种“气泡”或“口袋”；这自然要花费能量。此能量取作正比于袋的体积：?E=4/3πR³B；其中B为“袋常数”。

人们已经把各种附加能量加之于夸克波函数，但这里简单的能量式子还是很好地表明了基本思想。参量B是如此选择的：当袋的能量随着R缩小到最低值时，它即为核子的经验质量m_n 的c²倍——m_nc²。可以看出，式中R³项使袋不会扩张得太大；而1/R项基本上就是动能项，它使袋不致萎缩。

—旦B具有上面说明的那种性状，E_袋在最小值附近便是R的相当平坦的函数，零点振荡必然变得重要；正在采用一些群去推导这些振荡方式。诚然，轮廓分别的表面形状（球形）或许是一种粗糙的近似，但这使介子与袋的耦合形式大为简化。

计算 MIT袋的一个重要优点是：它提供了明确的模式，由此可以进行计算——由袋的边界条件和能量缩小到最小值这一特性求出夸克波函数的确定表示。对于胶子交换，沿着前面描述的线索，可以更方便地予以处理：用袋波函数取代组元夸克的波函数。这里有一项重大的区别：一旦B已经确定使得能量缩小到恰当的数值，这个具有能量量纲的参量为

在袋模型中，张量相互作用以及自旋 - 轨道相互作用由胶子交换引起。由袋模型获得的一项重大收益是：把与禁闭有关的自旋 - 轨道作用项自然地囊括进来，而把大部分不需要的、因胶子交换引起的自旋 - 轨道相互作用摒除。

我们的讨论不那么精确，但有一点很清楚：颇为不同的SU（6）破缺图像是从袋模型中衍化出来的。SU（6）破缺图像需要六个客体。而两个上夸克和两个下夸克（上夸克和下夸克都有自旋向上投影和自旋向下投影两种），形成SU（4）四位一组。在我们研究的水准上，SU（4）并不破缺，因为这些夸克是被对称地加以处理的。在袋模型中奇异夸克带有一项输入质量——“流夸克”质量。奇异夸克的这种质量并非由式5确定；它是如此选定的：当奇异夸克取代核子里的上夸克或下夸克中的一个时，其质量就附加到狄拉克方程中的哈氏量上，由此而产生的Λ粒子的质量就适当地显示出来。

在量子色动力学这个基础性理论中，只有对零质量客体才容易实施其手征对称性。因此，从零质量的上下夸克着手研究的袋模型具有很大的优越性。但即使是唯象的描述，它也并不比质朴的组元夸克模型更好。

手征协变性和π介子

通常，把式中的ψ（x）代以夸克波函数ψ_Q（x），即可把此式转换成夸克波函数的轴矢流。

这使我们产生一个问题。对于MIT边界条件，轴矢流的法向分量决不为零。但在袋的边界，轴矢流又无处可走，因为没有东西带着它离开口袋。显然轴矢流不能守恒，方程7不能成立。

这样的困难实际比上述情况普遍得多。当零质量夸克被边界反射形成驻波时，其手征量改号。但体系的手征量是守恒的，某一种东西会携带手征量通过物理真空；如果那种东西扩展到禁闭区外面，那么它必须是无色的。普林斯顿大学及其高级研究院的柯蒂斯 · 卡兰（Curtis Callan）、罗杰 · 达希恩（Roger Dashen）和戴维 · 格罗斯（David Gross）提出：禁闭区外的π介子也带有轴矢流。

在早期涉及核子和介子的手征理论中已经搞清，就π介子场Φ_π而言，用特殊的模型可以将其轴矢流写作

π介子压力 利用戈尔德 - 伯杰 - 特雷特曼（GoId-berger-Treiman）关系式f_π=g_Am_π/2f（其中g_A是轴矢耦合常数），可以很快地把π介子弱衰变常数f_π变换为π介子 - 核子强耦合常数f（f²/4π的实验值约为0.08）。利用这个在任何具有手征协变性的理论中都成立的关系式能够证明，袋外的π介子场，只要适当地量子化，或许便是从过时的汤川理论中的π介子 - 核子的赝标耦合中产生的普通的π介子场。因为π介子只存在于袋外，袋充当π介子场的一种宽展的源。这种带有介子耦合以恢复手征对称性的模型称为手征袋模型或云状袋模型。按照该模型的框架，理论物理学家们已经作过许多计算，特别是一些涉及π介子 - 核子相互作用的计算。

由于π介子只与非奇夸克耦合，故而π介子云与枝子的耦合比与奇异重子的耦合强得多。π介子云对内部禁闭区域存在一种压力——“π介子压力”。因为对于核子的这种压力比对于其他重子的大，所以它使核子收缩得比其他重子更小，完全可能是：核子是很小的客体，半径不到1费米；而级联粒子Ξ^-和Ξ⁰的半径可能为1费米。

固然，我们将其作为场处理的π介子，正如核子那样，具有夸克 - 反夸克次结构，但对于建立π介子机制及计算核子间π介子交换的相互作用这些目的来说，把π介子当作场来处理乃是适宜的。只要波长比π介子的夸克 - 反夸克次结构的尺度大，这样的处理方法是合理的。并且如此处理还可用上面说明的简单方式实现手征对称性；从而还引起π介子与核子的耦合。

因此，π介子云原来就是手征对称性的自然结果，π介子必然从核心取得手征特性。我们回过头来看原先的图像，其中把核子的整个实际存在范围认为是夸克核心和π介子云。用袋模型计算时，总的均方根半径并不精确地受云与核心交接处的半径的影响。假使没有介子云，便郞会得出太小的质子电荷半径。与此类似，总磁矩——核心和云的磁矩，不受交接半径影响。因此，必须通过另外途径考察，以获取关于核心大小的信息。

前面提到过，组元夸克模型给出基态核子半径为0.45费米，而其激发态半径为0.5费米。在袋模型框架中的类似计算则给出奇宇称激发态的袋半径为0.7费米，或其均方根半径为0.4费米。这些数值比从唯象的量子色动力学得出的相应数值大一些，

核子间的力

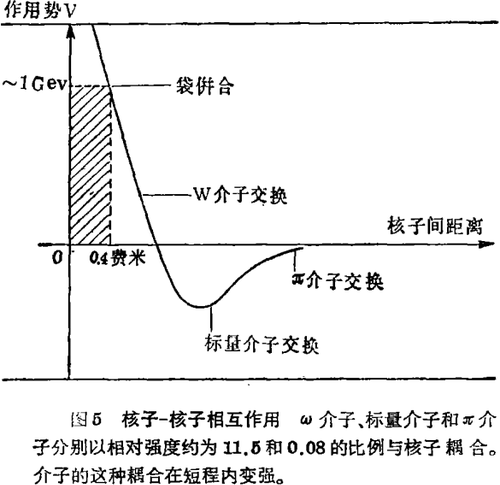
介子云包围夸克小核这样的图像，能消除某些概念上的困难，这些困难是在MIT大袋模型应用到原子核内的相互作用时遇到的。一旦使π介子与核子袋耦合，便简捷地重新建立起早年已发展的玻色子模型，因为可以依据π介子耦合方式来表示其他玻色子的耦合。

图5表示核子 - 核子相互作用，它的一个重要特征是指由ω介子交换引起的强斥力作用。尽管这种相互作用随着核子间距离r₁₂的增大迅速减弱，当r₁₂=0.4费米时它取值1 GeV左右，但当r₁₂=1费米时，其值还是明显可见。当然，在袋模型一类计算中，若夸克袋开始相互并合，ω介子交换势便开始截除；但这是一个渐进的过程，一部分斥力在近距离上依然保留下来。与袋内由微扰的胶子交换引起的相互作用相比，这部分斥力残余所扮演的角色更为重要。

原子核内的袋并非在无关联地自由运动，这是因为由矢量介子交换产生的高强度斥力使它们彼此分离。故而不能认为：若袋半径是R_袋，原子核内核子间的平均距离是r₀，袋彼此交迭的几率便为（R_袋/r₀）³。实际上因袋之间强排斥势产生反关联作用，其交迭几率会小一些。当然，能量更高，密度更大，核子核心区的斥力势垒就会被克服。但是这种转变必须平缓地发生，其物理性状不出现突变。至于为什么排斥作用的精细行为在两个袋相互并合后保留下来，这一点尚需确定，如许多论文的作者所提出的那样：这是否是由夸克 - 胶子的微扰交换引起：抑或由π介子的非微扰效应产生？此结论留待寻求。

由夸克次结构产生的效应在低能核物理中可能难于看到或辨认。不仅是因为核子的夸克核心的半径与原子核内核子间的平均距离（约为1.2费米）相比很小，而且由矢量介子势引起的斥力作用往往使夸克核心彼此分离。因此可以理解为，两核子的相互作用可用玻色子交换模型进行很好的说明，该模型在短距离上须加以调整以考虑夸克核心的行为。当然，我们似乎已把核子的夸克结构模型在描述低能原子核现象时降到次要的地位，但该核子结构模型提供了一种截断玻色子短程交换势的合理机制，这颇为重要；使相互作用保持有限。

［附注1] 术语简释

渐近自由：非阿贝耳规范理论的一个特征，在该理论中，相互作用因距离的缩短或动量的增大而变弱。

手征对称性：与零质量费米子（夸克）相联系的一种对称性。

手征SU（2）× SU（2）：与零质量夸克的两种“气味”有关的手征对称性；上夸克和下夸克当其质量被忽略时便显示出这种对称性。

组元夸克质量：非相对论性夸克模型中出现的一种有效质量。

流夸克质量：作为一些流代数关系式中以及量子色动力学拉氏量表式中的某些项而呈现的质量。

下夸克：一种轻夸克（比上夸克略重一些），其同位旋为1/2，同位旋的z分量为-1/2，电荷为-1/3e。这种非奇夸克与上夸克一起，同是核子的主要组元。

戈德斯通模型：该模型表明一种连续对称性，它在真空不具有同样的连续对称性时产生，此对称性的实现方式被称作“自发破缺”对称性模型。

螺旋性：分左手螺旋和右手螺旋两种，用以描述粒子相对其动量方向如何旋转。

“小”袋：一种强子袋，预言它具有一禁闭半径，比由电子散射测定的典型强子的电荷半径小得多。

量子色动力学（QCD）：涉及带色胶子和作为基本组元的夸克在内的强相互作用的非阿贝尔规范理论。强子是夸克的束缚态，其粘合力由胶子传递。

奇异夸克：一种有质量夸克（虽然在粒子物理中还被看作很轻），其同位旋为零，电荷为-1/2e，奇异数为1。这种夸克是超子的组元。