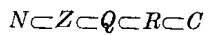引 言

世界古代数学史记载古代中国人研究自然数并创造了2个典范的数型图：第一个是河图，第二个是洛书〔1，2〕。自然，后者是以前者为先导而发展的。这两个图阵的创造显示出古代中国人在几千年前非凡的数字抽象化能力。这两个图阵标志出在漫长的岁月中人类数学思维发展出的两大类型。虽然过去从无人用现代数论观点来解释这两个图，它们仍然是纯粹数学中最早的两个数字模型图。

两千多年来，世界数学家将洛书发展为幻方〔3，4〕，并且一直维持这种解释到今天。作者认为：在对中国古代文化的继承、重整与发扬工作中，通过现代数论的见解，重新研究河图和洛书的数字分析是必要的、有重大意义的。

作者就三个方面探索洛书的数学本质：代数运算、几何构形与数字分析。研究报告的第一篇：《洛书矩阵论》摘要载于本刊1987年第五期。第二篇《洛书数字几何学导论》载于本刊1991年第三期。本文为该系列研究报告的第三篇，论述了以现代数论研究河图、洛书的数字分析。

一、《河、洛》数论研究的必须基本概念

数论是研究各种数集的结构、性质与运算函数的数学科学。它是一种“多方位”的学科，亦即不同的数学分支需要不同的数字理论。这里，我们首先引用数论中的一些基本概念与定义，作为剖析河图与洛书的工具。

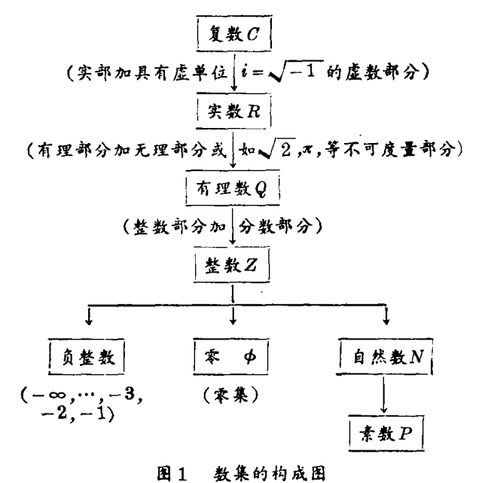
1. 数系 现代数学中，对数系的分类是从最广的复数集合（C）开始，从而循序地界定出：实数子集（R）、有理数子集（Q）、整数子集（Z）与自然数子集（N）……。其流程如图1所示。

我们看出：自然数集N是其他各种数集的基础。

即：

自然数亦称为正整数，它起源于未分割的数（也就是中国古代的‘绳结计数’），它是一切数理逻辑和公理的基础，也是数学归纳法的适用范畴。

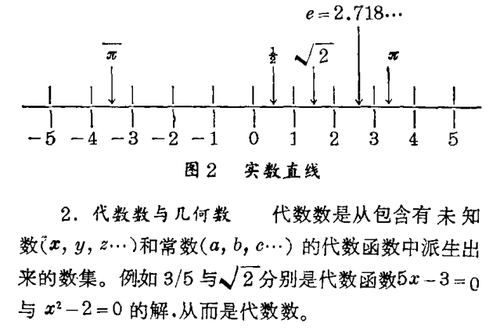
在实际应用中，我们采用实数。实数的重要性质之一是它们可用如图2所示的实数直线上的点来表示。对实数集中每个实数而言，它与实数直线上的点集之间均有一一对应的关系。数与点间的对应概念还可以超越直线推广到一个平面及空间。

凡不能表示为代数多项式之解的数，吾人称它为超越数，例如x与e。

我们也可以使数系匹配于几何坐标系，因而产生被称为矢量的几何数。例如用二重序偶（a，b）或（x，y）表示二维平面中的矢量，用三重实数（a，b，c）或（，x，y，z）表示三维空间中的矢量。同理，用n重实数（a₁，a₂，…a_n）可表示n维空间的矢量（或张量）。

3. 封闭运算   封闭运算是存在于数集的元素间的一个二元算符操作（加、减、乘或除），通过运算后生成的数仍在该数集之内。例如S是任意一个数集，我们定义S在加法下是封闭的，如果对S内的任意两个数a与b，它们的和a+b也是S内的一个数。我们可以看出、自然数集在加法下是封闭的，但奇数数集｛±1，±3，±5…｝在加法下就不是封闭的。

同理，可以分别定义在减法、乘法、除法下封闭的数集。数集可以在1个、2个…直到全部四个算术运算下是封闭的。例如在加法和减法下封闭的数集称为模（modul），在乘法下封闭的数集称为芒（ray）；在加、减、乘法下均为封闭的数集称为环（ring）；而在所有四种算术运算下封闭的数集称为域（field）。有理数集、实数集与复数集都形成域，但整数集不是域。

4. 数域与域的公设 除了上述定义，我们对数域亦可定义为：一个域F是其中元素用F内的二元加法与乘法组合成的数集F={a，b，c…}。（这里的加法与乘法是‘广义的’，即已包含有减法与除法。∵a+（-b）=a - b，a · 1/b = a/b）

在本文中，我们采用实数集作为建立其他数域的总集。在数域F内、下列公设应能成立：

a. 封闭律：F内的每个序偶（a，b）以及a+b与ab均属于F。

b. 加法交换律：对任意序偶（a，b）,a+b=b+a

c. 加法结合律：对任意三序组（a，b，c），a+（b+c）=（a+b）+c

d. 乘法交换律：ab=ba

e. 乘法结合律：a（bc）=（ab）c

f · 分配律：a（b+c）= ab+ac；（a+b）c = ac+bc

g. 存在着一个零元素O，使得对F内的任意元a，有a+0 = 0+a = a。我们称O为关于加法的恒等元。

h. 存在着一个单位元素，称它为1。使得对F内的任意元a，有a · 1 = 1 · a = a。我们称1为关于乘法的恒等元。

i. 对任意a ≠ 0，在F内存在一个元素x使得ax = 1，吾人用1/a = a^-1，表示这个x，并称它为a在乘法下的逆元素。

以数域的定义与它的二元运算为基础，数学家建立了线性函数、线性空间的概念，从而奠定了线性代数、线性几何与线性数论等近代数学学科。

5线性函数 最简单的线性函数的表达式为：

y=f（x）=ax+b

它由数域中的两种封闭运算（加与乘）组成。它的几何图形即直线。它是最重要的一种函数，因为一切光滑曲线均可由多段近似的直线段组成。另外，它与复数Z=ai+b具有同样的形式。

多变量线性函数的表达式为：

y= a₁x₁+ a₂x₂+……+a_nx_n+c

如常数项c=0，则该线性函数称为齐次的。

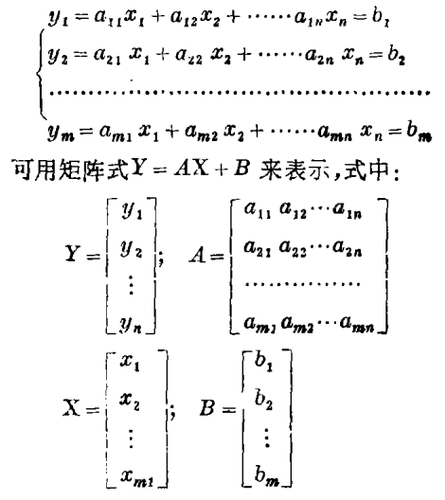
对线性函数组：

线性函数组的性质仅与系数矩阵A=[a_ij]有关。因而系数矩阵A可称为该函数组的代表矩阵。例如吾人可将洛书作为线性函数组中的代表矩阵。

6. 线性空间 线性空间的定义为：具有任意性质的一些元素的集合，元素间的和与‘数乘’积均有实质意义，并仍在该集合内，且满足确定的公理。

设X、Y、Z是该线性空间的元素，而1，C₁，C₂是一个数域中的数，则下列公设成立：

a. X+Y=Y+X；

b. （X+Y）+Z=x+（Y+ Z）；

c. 1 · X=X；

d. C₁（C₂X）= C₁C₂X；

e. C（X + Y）=CX+CY；

f. （C₁ + C₂）X= C₁X+C₂X；

g. 存在一个零元素O，使得对每个X合于X+0=X；

h. 对每个X存在一个负元素-X，使得X+（-X）=0

在现代数学中、许多数学实体例如算术级数、代数多项式、矢量、矩阵、微分和积分方程都可以是线性空间的元素，但是最普遍的线性空间是矢量空间。因为两个矢量之和以及一个矢量的‘数乘’积仍是该空间中的矢量。

在讨论矢量空间时、要引入矢量的线性相关与线性无关的定义如下：若矢量v₁，v₂…v_m中至少存在一个是具余矢量的线性组合（由加与乘的操作组成），则矢量v₁，v₂…v_m为线性相关的。反之，则称为线性无关的。

不难看出，矢量v₁，v₂…v_m成为线性无关的必要与充分条件是：只有当a₁=a_2=…=a_m=0时，关系式a₁v₁+ a₂v₂+…+ a_mv_m=0才能成立。

线性空间必须由一些线性无关的矢量张成。如一个矢量空间V由n个线性无关的矢量e₁，e₂…e_n张成，则我们定义该空间的维数为n、并记作dimV=n，而序列｛e₁，e₂…，e_n｝称为V的一个基底：e₁，e₂…e_n为基矢。V中任一矢量v∈V必为｛e_i｝的线性组合，即

v=a₁e₁+ a₂e₂+…+ a_ne_n，吾人称n序组（a₁，a₂…，a_n）为v关于（e_ⅰ）的坐标矢量。

基矢可用矩阵的行或列来代表。因此三维线性空间可以用3×3的矩阵为代表的三个行（或列）基矢张成。例如直角坐标的三维空间可用矩阵式：

来代表，其中e₁ =（1，0，0）；e₂ =（0，1，0）；e₃ =（0，0，1）三者组成单位基底。

因篇幅所限，上述仅为线性空间的一些基本概念。作者现将它作为一般公设，推论出数学中的同构原理如下：自然界中，任何线性空间V的构成必须建立在一给定的数域K上。每个n维线性空间不论它构成元素的特质为何，吾人均可按照行（列）矢量空间的加和乘操作，不加区别。在数学中、当将物体构成的两个集合按照同一运算系统可以得出等同的性质时，吾人称之谓“同构”（Isomorphism）。所有n维线性空间彼此是同构的，且同构于一个简单的模型，即行空间（亦即n序组）。这个事实可表述为一个定理：在域K上的一个n维矢量空间V中，任意选定基底｛e₁，e₂…，e_n｝就可确定V中矢量与Kⁿ内的n序组间一个一一对应关系，这个对应就维系了矢量和与数乘运算，从而V与Kⁿ是同构的。关于矢量分析、矩阵论与线性代数方面的系统知识，读者可参考有关专著[5、6、7]。

二、河图与洛书的数字分析

1. 对河图与洛书之检察

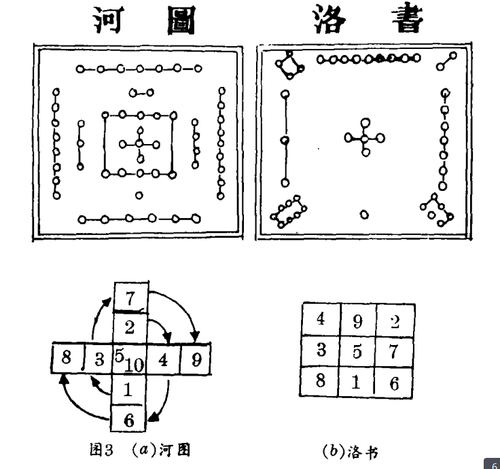
河图、洛书以及它们的数型图分别如图3 a与3 b所示：

由直接观察我们看出古代中国人用点表示整数。河图系由1到10的10个整数的集合组成，并分成一些方环：中央数是5，绕5的第一个内环由两个5作成的10组成，中心的5与10组成该图的核心部分。第二个环由1、2、3和4组成、加成另一个10。第三个环由6、穴8和9组成，加起来正好是300因此我们可将河图看作是由人们的两手十指所表示的解析模型，它实际上建立了基数为5的数系，而且也表示了基数为10的十进制数系的创始。

再则，该图用白点表示奇数1，3，5，7，9；用黑点表示偶数2，4，6，8，10。这表明将整数分为如图中箭头表示的奇级数与偶级数。而最有意义的是：河图模型显示了两个值得注意的形象：ⅰ）数被排列成古代中国人命名为‘纵横图’的位置，这意味着水平与垂直坐标。ⅱ）数被分为五个序偶（1，6）；（2，7）；（3，8）；（4，9）；（5，10），古代中国人称其为纵横数，这意味着数的行或列。因此我们可以将河图看作为表示坐标系概念的最早的数字模型。简言之，我们可以说：“在中国文明的初创阶段内，古代中国人创造了河图用来表示他们的数学思维的精华”。

现在我们转向洛书并将它作为古代中国文化内数学思维发展中第二阶段的结晶，洛书的结构是崭新的且全与河图不同。洛书仅用从1到9的9个数组成，并排列成被古代中国人称为“九宫”的9个胞腔的正方形，如图36所示。洛书最突出的特性是每行每列与两条对角线上3个数字之和都等于15。根据洛书的这一奇幻特质，从13世纪开始，数学家们就将洛书发展为幻方，但直到今天，洛书的实际数学内涵却完全被幻方的框架形式所掩盖了。

进一步解译河图与洛书中的数学关系、并建立“河洛数论”的根源，就是本文的主要目的。

2，河图的数字分析

我们从由n= 0，1，2，3…∞构成的自然数开始，正整数集N由算术函数f（n）=n+1所形成，表作N={1，2，3，…}。集合N还包含O作为它的子集，因为O是每个集合的一个子集。集合N被称为归纳集（Inductive Set），因为它具有两个特征性质：ⅰ）1∈N及ⅱ）若）a∈N则（a+1）∈N。集合N按照它的元素间的不同泛函关系可以分成许多分部，如由f（n）=2n给出的偶数集合、由f（n）=2n+1给出的奇数集合，由f（n）=n²给出的平方数集合等等。

应用河图数集，我们可确定其间的泛函关系，并可确定河图数集与整数数集间的命题函数。阐述如下：

A. 河图数集间的泛函关系。让我们将河图取作由H={1，2，3，4，5，6，7，8，9，10｝表示的数集。由直接观察我们看出H可作为万有集，因为它可以分为两个不交的与穷竭的子集：一个是用H₀={1，3，5，7，9｝表示的奇数子集，一个是用H_e={2，4，6，8，10｝表示的偶数子集。H_e与H₀是不交的因为H₀∩H_e=?（?是空集），H_e与H₀又是穷竭的因为H₀∪H_e= H₀因此H₀与H_e是彼此互余的。根据集论，一个集合A的元素间的关系R可以通过命题函数P（x，y）来建立，其中一个P（a，b）给出属于A×A的一个序偶（a，b）。所以、关系R是一些序偶的集合而它的构造表示式是R={（x，y），y=f（x）,x，y∈A}。用来观察河图及其数集H，我们看到河图由5个序偶组成，且它的泛函关系式为：

R_h={（1，6）；（2，7）；（3，8）；（4，9）；（5，10）}={（x，y）:y=x+5，x，y∈H}

换句话说，从H集我们可以建立一个关系子集：S={（x，y）；y=x+5 }，它的解集是｛（1，6），（2，7）；（3，8）；（4，9）；（5，10）}。由于解集的所有元素均在H内，所以关系R_h的定义域是这些序偶的全部第一个元素的集合，即d={1，2，3，4，5}，而R_h的值域是第二个元素的集合，即r={6，7，8，9，10}。如反转每个序偶元素的次序，我们得到逆关系：

R_h^-1={（6，1），（7，2），（8，3），（9，4），（10，5）} = {（x，y）；x=y+5 ，x，y∈H}

读者可在x - y平面上画出与R_h与 R_h^-1，我们看出R_h^-1恰为R_h的镜像。

最后，应指出河图数集的泛函关系R_h（或R_h^-1）对整个整数数集是普遍存在的。

B. 河图作为算术级数的二维矢量空间。—个算术级数具有形状：X={a，a+d，a+2d…a+nd，… }，其通项可以线性函数f（n）=a+nd表示，其中a为级数的首项而d是公差。此形式又可分解为：

X=（a，a，a，a…）+（0，d，2d…nd，…）=a（1，1，1，…）+d（0，l，2，…n，…）=ae₁+de₂

因此二级数e₁与e₂形成级数集合的一个基底。显然，两级数之和是一个级数，以一个纯量乘一个级数也是一个级数。所以级数的集合可形成一个线性的矢量空间。鉴于有限维矢量空间的维数等于基底矢量数，因而算术级数的矢量空间的维数为2。这个推理可应用于河图。

现在让我们取公差d=5，显然河图的核心部分代表5的倍数集，即H_c={…，-10，-5，0，5，10…}。而H_c是整数集Z的一个子集，H_c及其在Z内的其他陪集是：

我们既可把河图看作为算术级数集合的代表，因而可肯定河图数字能张成一个2维的矢量空间，这就阐明了为何该图内的序偶都用二元数给出。

对于一个二维矢量空间，它的单元基底为e₁=（1，0）与e₂=（0，1）。根据河图的特殊结构，我们取它的纵矢与横矢上最小矢量a₁=（1，2）与a₂=（3，4）作为它的最小基底。因而其他矢量均可表示为a₁与a₂的一个线性组合。（诚然，a₁与a₂必须是线性无关的。这一点很易得证，因只有当c₁=0，c₂=0时，式c₁a₁+ c₂a₂=0才成立。）。

C. 河图及以模5同余的商集。取线性函数y=mx+b的逆形式x=（y-b）/m时，就打开了同余算术的大门并建立了等价关系。我们用f（n）=（n-r）/m定义同余关系。其中m是模而r是余数。这意味着m是（n-r）的一个约数。将同余算术应用于河图数，吾人发现河图可表为模5同余的商集如下。

设R₅是由x=y（mod5）在整数集内定义的关系，读作“x以模5同余于y” 。表示（x-y）能被5除尽，从而R₅是数域Z内的一个等价关系，在商集Z/ R₅之内 恰存在五个等价类：

E₀={ …，-10，-5，0，5，10，…}

E₁={ …，-9，-4，1，6，11，…}

E₂={ …，-8，-3，2，7，12，…}

E₃={ …，-7，-2，3，8，13，…}

E₄={ …，-6，-1，4，9，14，…}

现在、每个整数x可唯一地表示为x=5q+r（其中r是余数且0≤r≤5），从而x是等价类E_r中的一个元素。由于等价类是互不相交的（即Z= E₀∪E₁∪E₂∪E₃∪E₄），因而商集Z/ R₅={ E₀，E₁，E₂，E₃，E_4｝阐明了河图的结构。

D. 河图与毕塔哥拉斯（毕氏）定理。毕氏定理（在古代中国曾被命题为商高定理）是数论中最普遍的典范例题之一。一般定义下的毕氏方程：x²+y²=z²是迪方丁（Diophantine）方程的一种典型。它包含有无限个整数解。吾人注意到这些解可分为两类：一类包含着一个基本解的线性倍数，从而所有的答案都是“相似”的（例如（3，4，5）；（6，8，10）；（9，12，15）… ）。而另一类则仅包含本原解，亦即x，y，z没有大于1的公因子（例如（3，4，5）；（5，12，13）…）。现在，我们可以说明为什么河图可同时提供这两类解。

首先，如上述B小节中曾指出的，河图的中央胞腔代表了算术级数H_c={5，10，15，20}，其中各项都是5的倍数，因此我们推出H_c为表示毕氏直角三角形关系的一个算术级数。例如从第一个三序组5²=3²+4²出发，可得到后续的解10²=6²+8²，15²=9²+12²等等。

其次，以P = {1，2，3，4，5｝表示河图的第一个方环和中心枢纽数的集合，我们可以证明P是毕氏方程的生成基底。用数学归纳法，我们可先建立形成方程x²+y²=z²的生成式是：x=m² - n²，y=2mn，z= m² + n²。其中m与n是整数并满足条件：ⅰ）m＞n，从而x是正的。ⅱ）m与n必须没有公因子，否则该公因子的平方数将被x,y,z所共有。ⅲ）m与n不能同为奇数，否则x与y将含公因子2。根据这些条件，我们得出关系式：

x²+y²=(m²-n²)² +（2mn）² =(m²+n²)²-z²

若我们令m与n取符合上述这些条件的所有可能值时就可得到全部本原解群。例如以P={1，2，3，4，5｝为基底生成数m与n的连续序偶时，则可归纳出连续的全部本原解如下：

根据上述推理，由归纳法得结论如下：ⅰ）毕氏方程对所有符合上述三个必须条件的整数都是真实的。ⅱ）河图数集H={1，2，3，4，5，6，7，8，9，10｝中的连续元构成m与n的基底连续序偶。

3. 洛书的数字分析 根据河图的数字分析结果，我们可直接地对洛书作出类似的分析，主要发现如下：

A.从河图到洛书。以河图作先驱，洛书为从1到9的9个数字构成3×3的9个胞腔的完全正方形，每个胞腔一个数字。中心枢纽数字仍然是5。四个河图序偶（1，6），（2，7）（3，8）（4，9）排列为这样的型序，使得正方形中的每行，每列与两条对角线上3个数之和都等于15。我们推出洛书可能是从河图创立的三阶幻方，并具有更深的内涵。

B. 洛书数间的泛函关系。让我们取洛书为由L={1，2，3，4，5，6，7，8，9｝表示的数集。L是一个有限集，它的元素数为奇数9。我们不可能将L如河图那样分成一些不相交的二元数子集；除了将L分为单元集外，仅有的可能是将L如洛书那样分为三个不相交的三元数的集合。

与前同理，在某一集A内我们可以建立一个命题函数P（x，y，z），心，就中P（a，b，c）给出一个属于A×A×A的有序三元数组。对集合L，它的泛函关系R_l可记作R_l={（x，y，z）；x+y+z=15；x，y，z ∈L}。通过观察我们可以解出尽的解集并将其分为三组：ⅰ）关于河图中4个序偶的解集S₁={（1，6，8）；（2，7，6）；（3，8，4）；（4，9，2）}。S₁的4个子集是既非不交的也非穷竭的，因为数5在该集中没有出现。ⅱ）关于枢纽数5的解集S₂，即S₂={（1，5，9）：（2，5，8）；（3，5，7）；（4，5，6）}。 S₂的4个子集是相交的因为它们都包含5。ⅲ）关于不交与穷竭的解集S₃={（4，9，2）；（3，5，7）；（8，1，6）｝或是其转置形式S₃={（4，3，8）；（9，5，1）；（2，7，6）}，前者S₃包含三个子集，它们是洛书的三个行，而后者S₃相当于洛书的三个列。

作为结论，我们说：洛书图阵就是将命题函数x+y+z=15应用于洛书数集L={1，2，3，4，5，6，7，8，9｝所得的解矩阵。

C. 洛书作为三维矢量空间的代表矩阵。在洛书中，三个行（4，9，2），（3，5，7）与（8，1，6）是线性无关的，因而可作为一个基底并张成一个三维矢量空间。我们称之为行矢量空间。类似地，三个列矢量（4，3，8），（9，5，1），（2，7，6）也是线性无关的，并张成一三维矢量空间称为列矢量空间。因而洛书可作为三维空间的代表矩阵。关于它的特性读者可参考焦氏洛书矩阵论^[3]与焦氏洛书数字几何学^[9]。

D. 洛书图阵与数的十进制。在数论中我们的数系是用一变元的代数多项式来表示，式中的变元就用作为数系的基数。十进制的基数为10并用下列多项式表示数

N=（a_n，a_n-1…a₁，a₀）= a_n10ⁿ+ a_n10^n-1+ …a₂10²+ a₁10+a。其中数字a_i可以具有从0到9的数值。由于0是每个集合的子集，我们可以取洛书图阵为数的十进制系统的数集。在上述多项式中每个数字的位置表示10的幂数，因而实数域的十进制结构如图4所示：

负实数作为正实数的镜像在零位线的下边。

E. 洛书与以模10同余的商集。作为河图的数字分析，我们曾证明每个整数x属于商集Z/R₅的一个等价类。同样，在十进制中我们必须用同余关系x≡y（mod W）表示整数间的关系。这个等价类集合用Z/R₁₀={ E₀，E₁，…E_9｝表示如下：

E₀={ …，-20，-10，0，10，20，…}

E₁={ …，-19，-9，1， 11，21，…}

E₂={ …，-18，-8，2， 12，22，…}

E₃={ …，-17，-7，3， 13，23，…}

E₄={ …，-16，-6，4， 14，24，…}

E₅={ …，-15，-5，5， 15，25，…}

E₆={ …，-14，-4，6，16，26，…}

E₇={ …，-13，-3，7，17，27，…}

E₈={ …，-12，-2，8，18，28，…}

E₉={ …，-11，-1，9，19，29，…}

通过m=10的同余算术我们可将整数集分为不交的组使Z= E₀∪E₁∪E₂…∪E₉，也就是说：洛书是商集Z/R₁₀的矩阵表示。

4. 洛书数空间的建立 在自然界中，一个空间是一些对象、事件或状态的连续集体所形成，在该集体中可能存在有一些维系各元间的关系。数学中可有许多种空间，例如欧几里得空间、非欧几里得空间等。这里，我们引进‘洛书空间’，因为在自然界中基础为1~9九个数字的离散数是到处存在的。正是离散数的存在能使吾人用加、减、乘、除四种运算进行数量操作来表达万有的现象。我们定义洛书空间为：洛书空间是由一系列数字集合所构成的数学空间。这些数字集合的组成是由从0到9的十个自然数及其相互间的加、减、乘、除运算的结果。洛书空间的具体代表是洛书图阵，后者也是所有数系生成元的一个有限集。

焦氏洛书空间的构成图已示于焦氏洛书几何学一文的图1。以该结构图为基础，我们看出纯粹空间的抽象概念可用三个子空间来表述：数空间、泛函空间与矢量空间。同理，在考察自然现象时，我们可以遵循三个途径：ⅰ）数字分析；ⅱ）代数演算与ⅲ）几何构形，而所有这三种途径都是由洛书空间的代表洛书矩阵所发展而成。

（待续）