它可以分析分形现象，压缩图像和声信号，追踪股票市场的波动以及从模糊的画面中恢复信息。这就是小波函数——数学上一个小的波形函数，通常含有一个中央尖蜂和两边上较小的负尖峰。大学和工业实验室里的研究者们正在狂热地发掘小波理论的潜在影响，而马萨诸塞州的一家新产业已宣布了具有特殊用途的小波变换集成电路块的诞生。

但与此同时，小波理论的开拓者们已开始谨慎起来，试图又过分兜售他们的工作而引起嫌疑。“它并不能解决宇宙间的一切问题，”AT&T贝尔实验室的数学家达贝姬丝（Ingrid Daubechies）评价说，“你必须了解自己的问题。”Schumberger-Doll研究所的数学家贝尔金（G. Beylkin）补充说：“要花上好几年的时间才能感受到它的影响。”他还说，尽管实质性的理论已经存在，但几乎大多数进行基本的小波运算的有效算法仍有待开发。

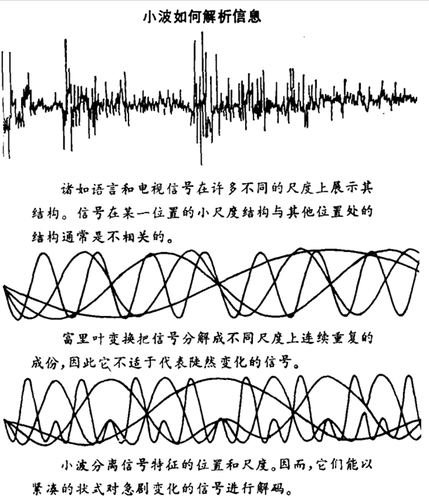
就实际问题而言，小波方法和富里叶变换类似，后者常按照频率成分或特征波长来分析信号。例如，富里叶变换能够恢复声音信号，这可通过不同成分的简谐波的迭加而实现。但是小波方法克服了富里叶变换在分析急剧变化的信号时的缺点。小波方法提供信号的各特征所在位置的信息：它可以探测和突出讲话音节的出现和小号音符的键击。

达贝姬丝已经帮助开发了一种适合于声音和图像处理的小波变换算法，明显快于最好的富里叶变换法。其复杂度仅与待分析的数据点的数目成比例，正被采用在剑桥Aware公司的集成电路块的制造中。这只是使用这个“大工具库”的开始，耶鲁大学的数学家考夫曼（R. Coifman）称。语言和图像识别，统计分析与湍流的模拟都可利用小波来作分析。

考夫曼自己的兴趣是一种新的“自适应小波变换包”，它能以一种特别紧凑的形式来表示信号。这种变换易于压缩，但更重要的是，它揭示了信号的结构。他说：“一旦你做了这种变换，你就会说到它的重要性。”他预测，比如说心电图的自适应小波变换能够帮助临床医生区别正常人和病人的心脏的跳动。

小波不仅仅能变换数据。按照贝尔金的看法，他们能够用来简化物理学家和其它学科中的专家们用于表示世界的数学变换。他说，采用小波变换能够把耑要10，000次运算的问题减少到100次运算——即能把上亿次的运算减少到仅百万次的运算。

然而将当前的小波技术用于这些新问题并不直截了当，贝尔金说。计算机只对极小的数据集才不致用尽存贮单元。达贝姬丝认为：小波理论家的主要挑战是把他们已在一维信号（如声信号）上取得的成功推广到二维、三维或更高维上去。她说，“简单的”多维变换受所取“偏爱方向”的限制；它们能够压缩主要含有水平和垂直边缘的图像，然而，比如，对角线边缘遗漏了。

达贝姬丝、贝尔金、考夫曼和其它研究小波理论的数学家们有点吃惊地看到他们的工作在这么多不同的方向迅速展开。考夫曼注意到，最初的洞见始于本世纪加年代初的纯数学，但从没传播到其它领域。

在80年代中期，马赛大学的数学家迈耶（Yves Meyer）告诉Elf-Aquitaine公司的石油工程师莫雷（J，Morlet），称莫雷偶然中重新发现了数学家的工作。只在这时研究者们才在不同学科间搭起桥梁。从此，发展一直很迅速，几乎在新的理论结果导出的同时就伴随着软件和集成电路块的研制。

考夫曼评论道，所有这些表明，小波知识从数学理论到应用的转换的延误是极小的。高斯（Carl Friedrich Gauss）在18世纪末发明了快速富里叶变换，但直到本世纪60年代初由贝尔实验室的两位工程师重新发现后才得到应用。他断言，应用数学和物理学几乎仍完全建立在19世纪的纯数学中。小波法可能是建立在过去50或60年间数学上的发展之开端。

［Scientific American，1991年1月号］