〔尽管社会科学仍然描述多于量度,然而它们却正在变得更为依赖数学了。最常用的一些技巧,近年来已经有了进展。今后,看来这些问题似乎更会激励新数学的产生。从数学上来说,社会科学似乎比物理学要远为困难些。这无须惊异,因为一个委员会的洽谈远比太阳系的轨道来得复杂。此外,社会科学家常常需要适于定性处理的而不是定量的数学。本文通过一些高度简化的模型,说明社会科学家,当他们不能作出精确的量度时是怎样去使用数学的。论题涉及从典型的商业决策直至森林中的狐兔生态平衡。在社会科学中这些初步的成果,使人感到数学为社会科学的服务将会愈来愈好。〕
数学和物理科学有着长期传统的协作,为了解决理论问题后者要求前者服务,前者也由此受到激励。许多第一流的数学就如此植根于应用。
数学和社会科学的联系是较为近期的进展,它仍处在一个萌芽阶段。但是近二十年来,一系列较高级的有希望的新的数学的应用已被提出。本文的目的是想阐明这个过程,这些例子、必然过于简单了,然而它们仍能传达一些这种新进展的风味。
在社会科学中,统计的重要性长期以来已为人们所认识,因此我们选择的是一些非统计的应用。
应用数学时的实际困难在于社会科学比物理科学复杂。也许,对于数学家来说,最感兴趣的问题是用当代的数学来刻划复杂的课题是否够用,如果尚不足,那么社会科学将可以成为今后激励新的数学分支兴起的源泉,如同物理学在历史上所起过的作用那样。
线性规划和博弈论
1940年由经济问题引出了两数学新分支:线性规划和博弈论。
一个工厂主提出的典型线性规划问题:怎样安排他的几种生产方式,使得利用他的资源能获得最大的利润。
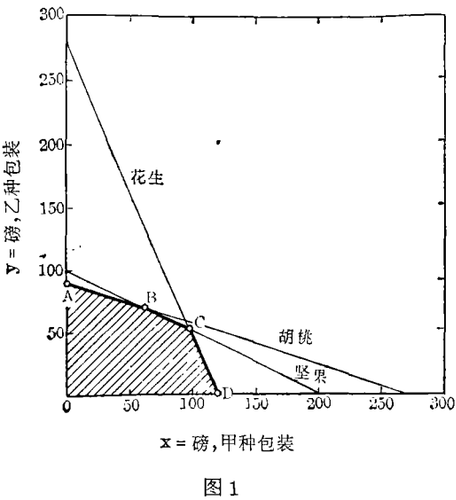
例如,果品公司包装干果零售。公司有84磅花生,40磅坚果和27磅胡桃。用两种包装:甲种包装由70%花生、20%坚果、10%胡桃混合;乙种包装由40%坚果、其余各为30%混合。甲种每磅售1.20元,乙种每磅售2元。目标是使干果混合后得到最大的总收益或最大利润。
我们首先来刻划零售过程。令x是甲种包装的磅数,y为乙种的磅数,显然
X≥0,且y≥0 (1)
甲种混合x磅中需要0.7x磅花生,乙种混合y磅需要用0.3y磅花生,因此我们要求
0.7x+0.3y≤84 (2)
同样地对于坚果和胡桃,相应地
0.2x+0.4y≤40 (3)
0.1x+0.3y≤27 (4)
这些条件表示在图1中,条件1意指解必须在x轴上方和y轴右方,条件2到4由三条线表示,每种情况解必须在线以下(或在线上),这就限制了解必定在阴影五边形区域内。
那么最大收益的解是什么呢?当然这要依赖于两种包装的价格,然而我们能作出某些一般的考察。在阴影区域内部选一个解是无意义的,因为“向上”移动能增加利润。因而我们可以把注意力限于构成上面边界的三条粗线段上。然而,原则上仍允许有无限个解——实际上是一个很大的数目。这里,对我们有助的是线性规划基本定理:一个最优解总在隅角处找到。因而我们仅需检验标以A、B、C和D的4个隅角。
通过简单的代数运算能找到这些隅角的坐标
A=(0,90); B=(60,70);
C=(98.2,50.9); D=(120,0)
相应于四隅角的收益为
A=180元; B=212元;
C=219.64元; D=144元
因此,C是最优点。
虽然这例子确实过于简单,但是许多重要的经济决策,可以用同样的数学技巧处理。假设一个商业公司有50个品种,使用100种材料,这就构成50维的问题,它有100个如同3条斜线那样的限制,我们虽不能够作此图,但是原则是相同的。高速电子计算机可以很容易的完成我们刚才描述的数量如此大的问题。
这些处理的只是一个工厂主的问题,如果在竞争中有两个或更多的商人参加呢?这就要回到博弈论,它是理想地适用于分析多人竞争情况的。
图 论
在社会科学中,一种普遍的反对使用数学的意见,是认为在社会科学中可供使用的材料只是定性的而不是定量的。但是能有效地处理定性材料的某些数学分支是存在的,例如图论。
让我们考虑一个点集、其中某些点可以用线联结,我们把每一根线看作为有方向的,在线上用一个尖头表示。因此两个点可以是不连通的、有一条连通道或有两条连通道的。如此的点和有向线段的集合叫做有向图。如图2所示的是有向图的例子。
图2a可以代表一个治安通讯网络。点1是司令部,点2和3是卡车班,而点4和5是不在镇上的巡逻队,可以想象所有的三种联络。在司令部和卡车班之间有两条连通道,在卡车和巡逻队之间有 ~ 条连通道,因为卡车能够找到巡逻队,同样地,巡逻队能招呼司令部,但是司令部不能直接找到巡逻者,两卡车班之间或两巡逻队之间没有直接的连通道。
这是一个强连通图的例子、因为每个人都能捎信给另一个人,反之亦然,虽然有时仅仅是简接的。例如一个巡逻队希望乘坐卡车,他要打电话给司令部,要他们用无线电通知卡车。图2b是连通的,但不是强的:1可以捎信给任何人,但是5即使通过中间力量也不能捎信给1。
有向图理论有着一大堆定理,其中许多是经常应用的,如通讯网络的研究。
再如。有几个家庭使用多部汽车去郊游,约定同一家庭的两个成员要分乘车辆,因此确定的车辆上的全体乘客必须来自不同的家庭,我们能达到目标吗?
当然我们需要知道各个家庭有多少成员和每辆车有多少座位。让我们令第i个家庭有Pi个成员,而第j辆车有Sj个位子,为了解出这个难对付的问题,让我们假设座位恰好够用。这用数学语言可叙述为
例如,我们有三个小家庭,相应地各有成员3、3和2位,我们有4部2座位的赛车,那么
P1=P2=3,P3=2,
而S1=S2=S3=S4=2
由于3+3+2=2+2+2+2,条件5满足,我们正好有这样一个座位数。我们注意min(1,S)=1,min(2,Sj)=2,min(3,Sj)=2对每辆车,因此对k=1,2,3写出条件6
k=1:3≤1+1+1+1
k=2:3+3≤2+2+2+2
k=3:3+3+2≤2+2+2+2
所有条件都满足。
使用图论能做到这些吗?我们可以把这个问题的解答看作由一有向图来代表。在图的左方是代表家庭的点,右方是代表车辆的点。每次一个家庭的一个成员被指派到一部车上,我们从该家庭的点到那车辆的点作一箭头。从而我们的问题就成为一个作图的问题。要求作出一系列从每个家庭的点为起点,而以指定的每部车辆的点为终点的线段。这样的图是否存在的问题已解决了。我们知道,如果家庭排列如后,以最大家庭为起始,以后次之等等,并且如果条件5和6满足、那么就存在一个解。例如3个小家庭和4部赛车的问题的解答表示在图2C中。
微分方程
微分方程在经济中有着许多应用。但是我们选了一个生态学的例子。
让我们考虑两类动物:狐狸和兔子,其中之一以另一为食源。给出它们的自然生长率和相互影响的效能后,我们对于这两类动物的生长能够说出些什么吗?
微分方程是理想地适宜于刻划一个给定量随着时间的消逝的变化的,例如,如果我们令x代表兔子在某一时间的数目,而且如果没有狐狸追猎它们,兔子将随兔子数成比例的增长,我们用
dx/dt=Ax (7)
表达之,或者说“兔子的改变率正比于兔子数”,数A由兔子的多育程度测定。
另一方面,如果y代表狐狸在某一时间的数目,而且如果没有兔子供它食用,那么狐狸将死亡,因此我们写
dy/dt=-py (8)
这里p是死亡率,负号表示狐狸数在减少。
我们可以假设兔子被杀数目正比于两个数的乘积这种被杀减少了兔子总数,但是有助狐狸数的增长。因此我们附加xy项到每一方程上去,对狐狸比例常数为正号,对兔子比例常数为负号,我们把模型写成形式
dx/dt=Ax-Bxy (9)
dy/dt=Cxy-py (10)
数A、B、C和p都是正的,它们必须由生态观察而建立。但是这个模型的有趣的特点是数学家即使不知道这四个常数的精确值还是能告诉生态学家许多信息的!
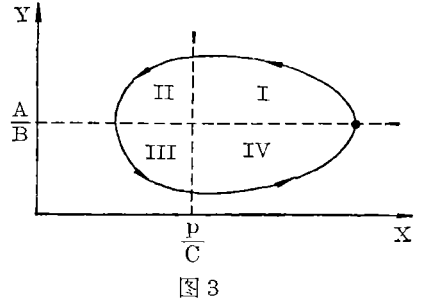
我们能够预示两个种类数如图3所表示的那样作循环的变化情景。我们绘制水平轴以表示兔子数,垂直轴以表示狐狸数。假设我们从一个以重点标记的右边的终点开始。在这个阶段,整个区域Ⅰ,狐狸和兔子都有丰富的食品,因此,狐狸在增长,但是由于周围有许多狐狸,兔子在减少。这由“向上而向左”的运动表示。当我们达到曲线的顶点时,兔子数已经成为临界数p/C意指狐狸已经没有足够的食物了,它们的总数都沿着斜滑线通过区域Ⅱ。在左边的终点,狐狸数为A/B,意指兔子已经开始增长了,这发生在整个区域Ⅲ中,最后当我们达到Ⅳ时,狐狸数又开始增长,直到开始点。然后,自然地再重复下去。
数p/C和A/B不仅对于模型中的变化来说是简单的,而且也指出了相应于兔子数和狐狸数的长项平均,因此两类动物数的摆动是依赖于这些按循方式平均的。数学理论无须知道精确值A、B、C和p就能反映出所有这些信息。如果我们知道了这些值,当然我们就能决定这曲线的长度和狐狸和兔子在每一阶段的预计数。
计算机模拟
高速的计算机是建立数学模型有力工具,通常过程大致如下。社会科学家收集了大量的数据,使他产生了某些一般性原则,这些原则如果用数学语言系统地表示出来,就提出了一个理论模型。数学将问题化成通常计算问题,而计算机正是进行这些计算的工具。
在许多情况下,理论上处理问题太复杂了,而其结果却十分容易理解,这时候,让计算机来模拟实际情形,以便我们在实验室条件下来研究它们,对我们就会很有用。
让我们以一个模拟模型来说明问题。一个大型百货公司有几百个售货员,五花八门商品,而顾客的要求又多种多样。百货公司能够收集到某一天顾客人数,他们在这一天到百货公司的时间以及他们想买什么东西,他们要求是什么等等统计上数据。现在想求出一般能符合顾客服务质量要求的最少售货员人数以及如何分配和调配这些售货员。从一般数学上的分析来说,这一问题是太复杂了,但却十分适合计算机模拟。
制订计划人员向计算机提供所有已掌握的顾客信息以及目前整个商店售货员分布情况。然后计算机查看了整个一年实际情况,指出哪些部门已经造成了不确当的排队现象,这样计划人员就调整一下售货员分布。如果当前服务质量太差,他可以增加售货员人数,要不然的话,如果他想节省一点开支,就得将人数略少于要求的售货员。然后,计算机再查看一下整个一年的实际情况,将结果报告出来。这样,通过不断试验和修正,就可以得到一个接近于理想的解决办法。计划人员在几个小时中就可以获得一般要花几年才能得到的实际经验。
这种模拟模型还可以用来训练培养新的商店经理,由计算机来模拟商店一个月的营业情况,当出现排队现象时,就由未来的经理来作决策。其决策又并入模拟情况之中。
偶然性在许多社会现象中起着重大的作用。因此,对现实的模拟应该包括随机的因素。在这一点上,现代计算机是十分理想的。下面我们叙述的例子,虽然和棒球有关,它却说明了社会科学家在模拟模型研究中所用到的技术。
这个例子是要确定棒球击球的次序对得分的影响(如果有这种影响的话)。将棒球规则,投手在垒区移动规则,和每个队员技术情况告诉计算机。以棒球季节中162场比赛为背景对这一模型进行试验。将详细统计资料保存下来,然后和洛杉矶棒球季节赛的记录进行比较。
由于偶然性的因素起了很大作用,结果并不完全符合实际棒球季节赛情况,但是其差异并不大于两个实际棒球季节赛之间的差异。例如,从模拟系统得到的整个棒球季节赛所得的总分是652,而实际上所得总分是640。但是,一般说来,棒球平均得分情况和季节赛实际情况十分接近。当然,这个模型还不完整。例如,棒球赛中偷进入垒区等在模型中都是不允许的。
之后,在这个模型上,先对10个棒球季节赛,然后对70个棒球季节赛试验了各种击球的次序。只是在经过相当长时间计算之后,后者才出现了明显的差别。
从这个模拟例子中可以得出相当有趣的结论。击球的次序并不带来什么影响。
这个例子说明了这个方法的实际作用及其严重的局限性。模拟方法很快可以使我们感觉到哪些是重要的,哪些是不重要的,哪一种战略是可以采用的,而那一种战略则是错误的,但是,这里我们必须记住,由于偶然性在这里起了一定作用,如果其它任何因素都不变化的话,同一模拟模型第二次试验会产生不同的结果。但是这里仍有一定经验可循。如果相同模型在相同假设条件下在计算机上多次运行,其结果之间的差别使我们对偶然性所起的作用有一个大致的估计,只有当策略上改变所引起的差别比偶然性所引起的差别远为大时,以模拟模型为根据所作出的决策才是合理的。
马尔科夫链
科学发展到高级阶段有一共同的特点,即组成理论的概念并不和现实世界发生直接联系,这一点在物理学中尤为突出。在社会科学中却很少有处于这种抽象阶段的理论,但是Estes-Burke模型却是属于这种类型的理论。
这一理论用来预测处于非常简单环境下人或动物的行为。每次试验中被试验对象有二个动作可供选择,其中一个动作被规定为正确的或者事后对试验对象给予一定“奖励”。奖励的方法随每次实验而异,我们的目的是要估计被试验对象对实验从长远角度看其反应究竟如何,这个模型成功地解释了大量被试验对象在各种各样奖励方法下的一般反应,有些结果是相当惊人的。
下面我们对模型略微详细解释一下。我们把二个可以选择的动作标为A和B。假定有一组影响被试验对象动作的刺激因素,我们把这些刺激因素理解为理论上各种条条。在每一阶段,其中一些刺激因素置成条件2(即促使被试验对象选择动作2)而其它刺激因素置成条件B。当被试验对象即进行选择时,他根据简单的随机方法选择一部分刺激因素。如果其中a个因素为条件A而b个因素为条件B,则他选择A的概率为a/(a+b)。因此,如果我们知道刺激因素的当前状态,那么我们就能预测被试验对象做动作A的反应的概率。
但是被试验对象如何从中接受教训呢?如果对反应A给奖励,则他在决策中_所用到的有刺激因素都变成条件A。这样,反应是A的概率就增加了,如果反应A是个错误选择,即没有对反应A给予奖励,则这些刺激因素都变成条件B,从而减少了反应是A的概率。
这是一个随机(概率)模型的例子。它并非要精确地预测某次试验的反应究竟如何,而是给出了每一个可能会发生的结果的概率,它可以用来估计许多被试验对象一般的行为或者估计从长远看来的反应。显然,这里一定要用到数学中概率理论,但是如何用呢?假定实验员决定对一半是A的反应给予奖励,而对反应B不予奖励。如果我们知道刺激因素的初始条件,我们就可以知道每一种反应的概率。我们知道奖励的概率,从而我们也知道被选到的刺激因素下次置成条件A或B的概率。
我们感兴趣的是在某特定时刻有多少刺激因素置成条件A。上述推理告诉我们,虽然我们不知道每次试验中这一数目是如何改变的,可是我们知道下次挑选到刺激因素的概率。这样,我们就有了一个随机过程,即对系统当前状态的了解完全决定了下一次的各个概率。这个过程称为“马尔科夫链”。
首先,我们猜测对刺激因素置条件存在着一个平衡,而且会达到这一平衡。这里所说的平衡是随机平衡,和力学中所遇到的平衡是截然不同的。它并不是说刺激因素趋于某一分布——例如说,2/3置成条件A,1/3置成条件B——而是告诉我们各种可能分布趋于一个平衡值。我们可以用大量被试验对象来说明这一点。如果对许多被试验对象进行相同实验,我们可以估计经过大量实验后他们分布的百分比究竟如何,从而我们可以估计期望他们给出反应A的百分比。
另一个同样令人感兴趣的猜测是估计期望某一试验对象给出反应A的概率。让我们用前面例子来说明这一点,在这个例子中实验员对一半是A的反应给予奖励,而对反应B不予奖励,如果被试验对象非常有理智并有选择最好方法的机会,则他每次都作出反应A。但实际情况并非如此,他2/3次时间作出反应A,而1/3次时间作出反应B,这一数字和我们从马尔科夫链模型中所得到估计完全一样。
马尔科夫链模型估计,被试验对象非自觉地调整着他作反应A的概率使之和A被奖励的概率完全一致。在我们例子中,设f是他作出反应A的概率,则他作出反应B的概率是1-f。实验员又做些什么事呢?由于对半是A的反应给予奖励,而在B反应之后,实验员则宣称A是正确的反应,因此实验员实际上按1/2f+(1-f)概率奖励反应A。要使它和被试验对象的反应相合,只有
f=1/2f+(1-f)
因此f必为2/3。
马尔科夫链理论对其它现象也作了估计。其中有一些是和上述例子同样惊人的估计,所有这些估计都已由实验所证实。
我们已经看到了数学应用到社会科学的许多例子。尽管其中大多数例子实在过于简单,这些例子却抓住了数学为其新的对象服务的方法。社会科学是多么希望数学的最新发现能为其服务1我们深信数学为社会科学服务将会越来越好。
[Mathematical Sciences第21 ~ 36页]