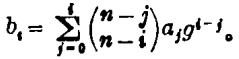十一世纪我国北宋贾宪的“开方作法本原”图和增乘开方法，是世界上最早出现的二项式系数表和高次方程的数值解法，比西方所获得的同样成就都早了数百年。这两项都是在世界数学史上的著名成就。

一般认为，增乘开方法由《九章算术》“少广”章中的开方、开立方术演变而来，至于如何演变，则未见详论。“开方作法本源”图（即贾宪三角）及随后出现的元代朱世杰《四元玉鉴》（1303）中的“古法七乘方图”仅可用于二项式xⁿ=c的开方。该种图表与增乘开方法（包括正负开方术）的关系如何，以往尚无明确的解释。为理清贾宪三角与增乘开方法的脉络，弄清二项式系数与增乘开方法的关系，本文从《九章算术》“少广”章着手，并对贾宪的“开方作法本源”图、“增乘法求廉草”，和朱世杰的“梯法七乘方图”，“古法七乘方图”进行研究比较，指出以下方面：

一、从系数方面来观察“少广”章中的开方、开立方术文，可知至少在一千八百年以前，在开方时已实际应用了二至三次幂的二项式系数，古代开方求次商以后的术文，就是二、三次方程求正根的增乘开方法。增乘开方法（包括正负开方术）就是在这基础上，扩充应用到求解四次以上的高次方程的。

二. “开方作法本源”图与“古法七乘方图”有许多相同之处（如数字的排列、中藏皆廉、左积右隅等），但“古法七乘方图”中的二项式系数是横排的、中藏的廉列在表下，又是不同的。总的来说“古法七乘方图”很明显地表示：从0次到n次幂的贾宪三角，分开来看是高次方程用增乘开方法经过减根后得出新的方程后，方程系数的前后变化规律；合起来看是前后两式的系数转换的关系表。即原式为a₀xⁿ+a₁x^n-1+…+a_n-1x+a_n=0，令x₁=x-g转换为方程b₀xⁿ+b₁x^n-1+…+b_n-1x+b_n=0，则系数的转换关系是

贾宪则在“增乘方求廉草”中用文字描述了这一关系。这是宋、元数学家在数学史上的另一卓越贡献。

本文把“少广”中的术文，结合现代符号，加以逐句对注，并作出增乘开方法的模式，与贾、朱两家的图、草进行详细的对比，来说明问题。