[编者按]计算视觉理论是当前世界视觉研究的主流,是计算神经科学的基础,它促进了心理物理学、神经生理学、计算机科学、数学、物理学、系统科学、工程学等联合起来研究视觉——大脑的信息处理过程与机制。
波吉欧(Poggio)等人提出的正则化理论是计算视觉的一个重大进展,通过算法将计算理论与生物硬件联系起来,为人工智能中的自动图像分析系统,视觉专家系统的研究奠定了理论基础,并成为研究脑信息加工的前沿领域。
霍普菲尔德(Hopfield)提出的神经网络集合运算的理论框架成功地求解了一类最优化问题,并研制出相应的硬件芯片,这对当前正在兴起的新一代计算机或智能机的研制具有重大指导意义。
波吉欧与霍普菲尔德的工作已引起人们普遍的关注和国际各智能学术机构的重视。为使读者对这些前沿课题的发展近况有所了解,特编译了波吉欧与霍普菲尔德分别在Nature与Science上发表的论文,供读者参考。
计算视觉是以视觉信息处理的理论研究为中心课题的,属于人工智能范畴的一个新领域。研究计算视觉的主要目标有两个:一是要开发能从图像输入数据自动构成场景描述的图像理解系统;二是要理解我们人类的视觉。
人们已经解决了初级视觉中的一些问题,并且成功地建立了一些专用算法。立体视觉匹配、视觉运动的计算、从运动恢复结构、由明暗推导形状、表面重建等,就是其中几个例子。最近出现的一个新的理论进展,是要在同一个理论框架下把上述大多数结果统一起来。这种方法来自人们对初级视觉问题的共同结构的一种认识。在本文中,我们将引入一种特殊的正则化方法,讨论它对计算机视觉和并行计算机体系结构的意义,其中也包括可能为生物视觉系统所采用的并行硬件。
初级视觉处理过程
初级视觉是由一组能从二维光强度阵列恢复三维可见表面物理性质的处理过程组成的,它们的组合输出大体上对应于马尔(Marr)的2.5维图。初级视觉模块的计算理论主要解决表象和处理这两个密切相关的何题,该理论必须说明输入和所期望的输出应该具有什么样的形式或表象,并提供把二种表象变换成另一种表象的算法(处理过程)。
初级视觉的精确定义是:它是光学成像问题的逆问题。经典光学或计算机图像学的基本问题是要确定三维物体的图像,而视觉则面临着从图像重建表面这样一个逆问题。由于在把三维世界投影成二维图像时损失了大量信息,因此视觉时时都要依靠自然的约束即关于客观世界的假设,才能获得确定的输出,找出并使用这些约束条件,这是在分析特殊视觉问题时会反复出现的问题。
运动的计算和图像强度突兀变化的检测(物理边缘的检测)是初级视觉中两个重要的问题,它们充分地体现了初级视觉问题的困难所在。测量局部运动只能提供速度矢量的法向分量,切向分量仍然是“不可知的”,因此估计整个速度场这个问题,一般说奔,单靠从图像中直接可获得的测量是无法完全确定的,视觉流的测量本质上是不确定的。边缘检测所遇到的问题略有不同,边缘检测指的是这样一种处理过程,它要从图像的强度变化找出三维表面的物理边界。其实这个问题就是对图像数据进行数值微分,但是在成像和采样过程中所不可避免的噪声却使微分运算处于困难的境地,微分放大了噪声,因此这个处理过程本质上是不稳定的。
不适定问题
一个问题是适定的,如果它的解是存在的,唯一的,且连续地依赖于初始数据。不适定问题则不满足上述判据中的某一条或某几条。从形式上不难证明,初级视觉中的一些问题,诸如体视匹配、从运动恢复结构、视觉流计算、边缘检测、从明暗恢复形状、光度计算、表面重建等,都是在Hadamard意义下的不适定问题。视觉流计算之所以是不适定的,是因为从一条轮廓线上的法向速度分量恢复整个速度矢量场这个“逆”问题不满足唯一性条件。边缘检测即数值微分之所以也是不适定的,则是因为解并不连续地依赖于数据。求解不适定问题即恢复“适定性”的主要想法,是引入适当的先验知识来限制容许解的集合。我们把任何一种使不适定问题适定化的方法统称为正则化。变分正则化是指在某一变分原理下重新表述一个不适定问题的正则化方法。如从“数据”Y中找到Z这样的不适定问题
AZ=Y (1)
正则化,就需要选择范数‖·‖,并选择一个起稳定作用的泛函‖PZ‖。在标准正则化理论中,A是一个线性算子,范数是二次的,P是线性的。可供使用的两种方法是:(1)在满足‖AZ-Y‖<ε的Z中找出使
‖PZ‖2 (2)
最小化的Z;(2)找出使
||AZ-Y||2+λ‖PZ‖2 (3)
最小化的式中X是所谓正则化参数。例
迄今在初级视觉中使用的大多数稳定性泛函都是Tikhonov型的,也就是期望解Z的前P阶导数的线性组合。表1列出了已经用变分原理解决了的几个初级视觉问题。
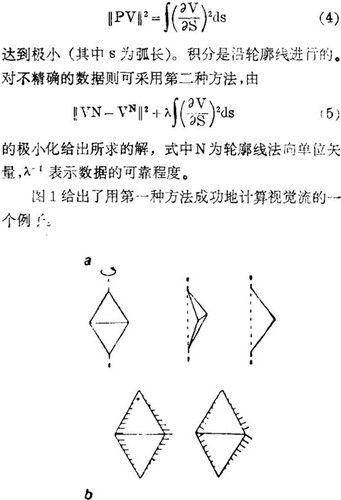
希尔德莱斯(Hildreth)对速度场提出了更一般的平滑性约束,在物理上这个约束基于这样的考虑,即真实世界是由表面平滑的固体组成的,而这些固体的投影速度场一般说来是平滑的。第一种算法是在测量速度矢量的法向分量之后,假设法向速度分量VN(s)是精确测定的情况下,使
物理上的合理性与错觉
对于正则化分析来说,头等大事是解在物理上的合理性,而不是解的唯一性。对一个问题以及对问题的主要约束所进行的物理分析,在正则化中起着重要的作用。在某些特殊情况下,正则解并不对应于具有实际物理意义的解,这时,为求解不适定问题而作的先验假设就可能被违背。在一些很一般的条件下,式(5)的平滑性假设可以给出正确的解。但是对于某几类运动和轮廓线,平滑性原理却无法产生正确的速度矢量场。人的视觉系统在这种环境中似乎也只能得出同样是不正确的速度矢量场,因此,这种现象有助于我们揭示大脑对外部世界所作的先验假设。
模拟网络
生物视觉的一个令人百思不得其解的谜就是它的高速度,对于这个问题人们总是提出平行处理作为它的理由。然而,由数字处理得到的计算模型却是不能令人满意的,特别是有越来越多的证据表明,神经元是一个复杂的装置,远不同于简单的数字开关。因此,研究一下初级视觉的正则化方法是否可以导致一种不同类型的并行算法,这是很有意义的。我们已经指出,一个线性的模拟网络(电的或化学的)乃是求解标准正则化理论所要求的变分原理的一条自然途径。
从变分原理到电学网络或化学网络这种映射的基本出发点是哈密顿最小作用量原理。可以用模拟网络进行计算的变分原理的类型由基尔霍夫电流、电压定律给出,这两条定律代表每一个网络元件所满足的保守性约束和连续性约束。一般说来,实现一个变分原理的网络可能不止一个,而是有许多个。例如,霍普菲尔德在解决联想记忆问题时所提出的那种级联网络也可用于标准正则化原理。
根据基尔霍夫定律可以证明,对每一个存在唯一解的二次变分问题,都存在一个与之相应的、具有同一解的,由电阻和电压源或电流源构成的电学网络。
从当前对神经元、膜和突触的生物物理学性质的了解来看,这种模拟的并行计算模型就特别有意义。一小片神经元膜就可等价于电阻、电容和现象学意义下的电感,树突尖端处的突触模拟了电压源,而大树突或胞体上的突触则模拟了电流源。因此,单个神经元或神经元的小网络就可实现正则化原理下的模拟解。
突破标准正则化理论
初级视觉的这一新理论框架清楚地表明了标准的Tikhonov型正则化理论的内在的优点和局限性。它的主要问题是:需要了解待求未知函数的平滑化程度。
标准正则化理论只涉及线性问题,其基础是二次型稳定器,由此得到的结果是二次泛函最小化和线性的欧拉 - 拉格朗日方程。为了加上正确的物理约束,可能需要非二次泛函(表1中从明暗恢复形状属于非二次泛函)。即使在这种情况下,标准正则化理论也还是可以使用的,但解空间不再是凸的,因而在极小化过程中可能会发现许多局部极小。有人已经提出了一个从深度数据重建表面时可以保持不连续点的非二次稳定器,其中加入了关于不连续点几何性质的先验知识(线处理过程),特别是由不连续点所构成的是一些连续的、一般是直的轮廓线这种先验知识。在标准正则化理论中,搜索空间只有一个局部极小,对这个极小,适当的算法总是收敛的。对非二次泛函搜索空间则好像是有许多局部极小值的“山脉”。最近已经有人提出了一些旨在解这类极小化问题的随机算法,以避免可能使简单爬山法陷入困境的局部极小,其基本想法有点像在搜索算法中加上一个噪声抑制项。如果有办法在一个非线性模拟网络中表达非二次变分原理,那么一个合适的高斯噪声源就可以驱动这个模拟网络。因此,系统的动态特性可以用代表扩散过程的一个非线性随机微分方程来描述。
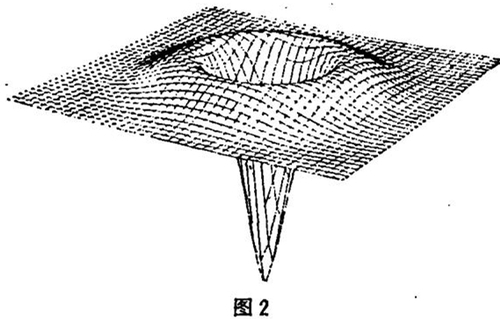
图2表示作过滤波处理边缘检测的一个正则化
视觉正则化理论现在所面临的挑战,是如何使它突破标准正则化方法的限制。可以用二次泛函来实现的计算,其适应性是很有限的。只要认识到对二次代价泛函的极小化只能产生一个线性正则化算子,也就是说,只能产生从输入数据到解空间的一个线性映射,我们就可以看清这一点。在数据都在规则的格点上且满足适当的条件这个特殊情况下,这个线性算子就可以变成一个卷积运算,也就是对数据作简单的滤波处理。与物理学中的线性模型一样,标准正则化理论在许多情况下是一种非常有用的近似方法,但它并不能解决视觉中的全部复杂问题。
用随机方法实现正则化
实现正则化的另一个严格的方法是在贝叶斯估计和马尔科夫随机场模型的基础上建立起来的。在这种方法中先验知识是用恰当的概率分布来表达的;而在标准正则化方法中,先验知识则产生对解空间的约束。以表面重建为例,先验知识可以用表面的一个马尔科夫随机场(MRF)模型来描述,在MRF中,每一个离散位置上的取值只依赖于一个给定的小领域中的值。在这种方法中,最佳表面使诸如MRF的最大后验估计或MRF的后验平均值一类似然性判据达到极大,已经有人指出,MRF的最大后验估计等价于式(3)那种一般形式的变分原理;式(3)中第一项代表数据与解之间的差异,第二项现在则是一个任意的势函数(定义在一个离散的网格上)。如果噪声是可加的、高斯分布型的,而场的一阶差分是零均值的、独立的高斯随机变量,那么在一般情况下,凡是非二次的全部变分原理都可以简化成一个标准正则化二次泛函。在这种情况下,最大后验估计(MAP)就符合所有的估计,特别符合后验平均值。但马洛奎恩(Marroquin)最近已经证明,上述结论在一般情况下并不正确:在大多数情况下,对自然的误差测量来说,MAP估计并不是最佳的,可以找到像后验平均值这种更好的估计。在这些情况下,正则化问题并不等价于寻找一个能量泛函的全局极小:不需要模拟退火过程而可以用一个Metropolis型算法来代替。
在希尔德莱斯的运动计算中,平滑化假设相当于假设在一条轮廓线上两个相邻点之间的速度矢量变化是零均值的、独立的高斯随机变量。随机方法与标准正则化方法之间的这一联系,使我们得以洞察约束特性和稳定器选择的真相。在解决视觉这个求逆问题中所使用的变分原理,就对应于能产生合理解集的马尔科夫结构。
在今后的研究中,与视觉正则化相关的一个领域是正则化算子的学习问题。在标准正则化条件下,把数据映射到解空间的相应的线性算子可以通过一种联想学习方法获得。这种学习方法是在研究生物记忆问题时提出来的。
向符号化的描述发展
迄今为止,我们讨论的都是初级视觉问题,在视觉初级阶段所产生的则是在观察者周围的三维物理表面的类图像 - 表象,从这些表象出发得到所谓本征图或2.5维图,还需要向前迈出一大步。本征图仍然是类图像数值表象,但还不能用物体来加以描述,它们已经足以应付像操作、导航这样一些视觉系统的高层次任务。但仍不能直接用它们来完成识别与描述任务,因为这些任务需要产生并利用更符号化的表象。首先,我们很难看出究竟怎样才能把符号表象的计算纳入不适定问题正则化的框架中去。
所有正则化方法的基本想法,在于约束由可能解所组成的空间,如果把这个空间约束在有限维,那么把求逆问题正则化还是很有希望的。因此,一个以分立符号的有限集为基础的表象可以使一个可能是不适定的问题正则化。从这个观点出发,知觉问题(使用关于外部世界的一般性约束,使一个原来是未加约束的问题正则化)实际上就等价于问题求解和推理这个经典的人工智能问题,也就是说,通过对解的搜索范围的限制,寻求解决难于对付的问题(例如弈棋)的途径。
结 论
我们提出了一类能自然转变成目前正在蓬勃发展的并行数字计算机体系结构的视觉算法,标准的正则化方法只要是充分的,就可以引出两类并行算法。一类是像最速下降那样寻找一个凸泛函极小值的算法,另一类则是为视觉计算发展起来的更有效的多格算法。这两类算法总是适用的,如果数据在一个规则的网格上给出,且式(1)中的A是空间不变的,那么这些算法就可以用卷积运算来代替。这时,通过数据与一个已计算好的滤波器卷积,就可以获得正则化的解。
所有这些算法、都可以用由许多彼此只有局部联系的处理器所组成的并行结构来实现。不能用正则化方法加以解决的问题,需要符号表象并对符号表象进行运算的问题,可能需要像目前正在开发的“联络机”(Connection machine)那样的具有全局通信设施的并行结构。
不适定问题的概念以及与之有关的老的或新的正则化理论,似乎为初级视觉中的大部分问题提供了一个令人满意的理论框架。这一新观点揭示了初级视觉问题的计算方面的(不适定)性质,在求解这些问题的算法结构和可用于高效视觉信息处理的并行硬件之间建立了联系。它也指出了初级视觉中迄今所使用的变分原理的内在的局限性,同时也指出了把正则化分析从标准理论推广扩大的途径。
(Nature,1985年第317卷第26期)