美哉物理(十一)
时间是少数几个最基本的科学概念中的一个。有哲学家说:“应从时间理解存在”;又有哲学家说;“由于运动,空间在时间中产生”。爱因斯坦就是从时间概念着手,创立了相对论以及相对论时空观,他认为:“空间和时间融合成为一个均匀的四维连续区”,四维时空依赖于物质及其运动而变更着自身的形式。这时间概念的深刻性,或许更在于由黑格尔所说明的、并为恩格斯所认定和进一步锤炼的“一个伟大的基本思想”,此乃指:“世界不是一成不变的事物的集合体,而是过程的集合体”。过程者,运动变化的时间进程;过程者,有可逆和不可逆之分。而物质系统的运动,循着怎样具体的过程演化,是一个疑难问题;但有一点可予肯定:时间之矢,演化所凭。科学家用“熵”的增减标志演化过程的方向,从而拓宽了热力学的范畴,也扩充了整个物理学的涵容、还促使其向自然科学的其他领域不断地渗透。藉此,伊 ? 普利高津*提出了耗散结构论,并将此认作是开始了“人与自然的新对话”。该理论为自然界的非生命物质系统、生命物质系统之进化研究提供了适当的解释;普氏还因这“新对话”而得到了“美感上的满足”。
时间反馈的对称和不对称
一般说来,线性动力学定律都具有时间反演变换的不变性,即当t→-t,其动力学方程的形式均保持不变。例如在经典动力学和经典电动力学里,牛顿运动方程包含位置矢量对时间的二阶微商项,电磁场传播方程也包含场量或势函数对时间的二阶微商项,它们对于时间反演而言都是对称的。相对论尽管变革了牛顿的绝对时空观念,但其时间反演对称性还是保留的。而量子力学里的薛定谔方程和狄拉克方程等包含带有系数ih的一阶时间微商项,当t→-1,且波函数ψ→ψ*,方程的形式也保持原样;这里ψ*是ψ的共轭复量,对微观粒子系统测量得到的是粒子出现的几率,此乃取决于|ψ|2=ψψ*,因此波函数的方程对于时间反演而言依然可认作是对称的。至于从具有普遍意义的拉格朗日方程来看,倘若拉氏量本身对于时间反演是对称的,则拉氏方程便显然具有时间反演变换的不变性;鉴于该方程的普适性,故而说一般的动力学系统都禀有时间反演的对称性,或谓之通常的动力学过程都是可逆的,似当无可非议。
力学运动的过程可逆,尚易于想象。譬如说,看地球绕太阳运转的录像片,若把片子倒向放像,感觉上并无异样,除了地球反向运转外,轨道是完全相同的。但看一花瓶摔到地上而碎裂的过程,假如倒过来看,则是地上的碎片拼合成毫无碎纹的完好花瓶、再跳回桌上;这当然不可理喻,因为如此过程不可逆,即不可能自发地逆转发生。
与动力学系统不同,涉及热现象的热力学系统的变化过程往往是不可逆的。孤立系统与外界无相互作用,所含能量则守恒;孤立的热力学系统的变化过程是绝热的;而凡自发地进行的绝热过程必定不可逆。德国物理学家克劳修斯(热力学的奠基人之一)引入“熵”概念,以表示自发的热力学过程的不可逆性。熵的德文原词Entropie 为克劳修斯所创作,乃取意于它与“能”(Energie)概念的密切关系;而译名为我国物理学家胡刚复所制定,乃取意于公式
dS≥dQ/T (1)
此式将熵S的改变量dS与热量的改变量dQ与温度T之商作比较。对于孤立系统的绝热过程,dQ =0,于是
dS≥0 (2)
如果过程可逆,dS= 0;如果过程不可逆,dS> 0。这就是凭借熵概念所阐述的热力学第二定律:孤立系统的一切自发过程总是使熵增大;该定律禁绝了熵减,故而这样的过程不可能逆向进行。其实,孤立系统从非平衡态趋向平衡态的过程总是自发进行的;一旦达到平衡态,熵取极大值,过程也就终止了。反过来,从平衡态回复到先前的非平衡态,确是不可能自发进行的。
统计物理的奠基人玻耳兹曼对宏观物质系统的分子热运动作出统计分布解释,为宏观热现象之热力学描述提供微观(这里指分子尺度)理论基础。他建立了分子速度分布函数所满足的“玻耳兹曼方程”,又提出了H定理。可以证明,玻耳兹曼方程对于时间反演变换是不对称的。而H函数与熵函数有简单的关系:
S=-kH+常数 (3)
其中k是玻耳兹曼常数。H定理则简洁地表示为
dH/dt≤0 (4)
此式对孤立系统成立,表示在这样的系统的自发过程中,H函数总是递减的;达到平衡态,dH/dt = 0,H取极小值。由(4)式可见,H定理把热力学过程的时间反演不对称表达得更为明晰。

图11-1
图11-1是玻耳兹曼的墓碑照片,碑上刻着墓主人导出的公式*
S= klog W (5)
其中,W为与宏观态所对应的可能的微观态的数目。W增大,S也随之增大,则就表明热力学系统的熵增过程,实际是状态朝着其出现几率渐次增加的方向演化、直至达到几率为极大的平衡态为止。所以,这个公式从微观意义上给出了熵概念的统计解释。也就是说,熵函数是系统之微观无序度的反映(或径直说,就是其无序的一种量度),熵增即为从有序向无序的演化过程。那末,如(5)式所定义的熵概念比克劳修斯等人的定义有更为深刻、宽广的涵义,这样的定义就为此概念超越平衡态热力学、超越物理学,甚至超越自然科学的应用留有广阔的拓展余地;因此,(5)式也许可算是玻耳兹曼的最大科学功绩。
熵增和熵减
英国物理学家爱J顿曾把熵喻作“时间之矢”;这“矢”之所向,便是物质系统的演化过程之方向。熵增意味着系统从有序向无序演化;那末,熵减又如何呢?物理学家大多偏爱对称化的思考方式,熵有增,似当亦有减;大自然恰恰如此,有熵增的过程,亦有熵减的过程。
自然界里的孤立系统并不多见,绝对孤立的系统毕竟太理想化了。而绝大多数是开放系统,即系统与外界有相互作用,有能量和物质的相互交换,亦即总有能流和物质流从系统边界流进流出,热流就是一种能流。随着能流和物质流的进进出出,系统的熵并不总是增大;也就是说,外界与系统之间还有熵流。可以把系统的熵变量分成两部分
dS=diS+deS (6)
其中diS即为系统内因无序度的增大而导致的熵产生; deS便是熵流。对于孤立系统,deS = 0,则dS=diS> 0;对于开放系统,虽然diS > 0,但deS或者大于零,或者小于零,分别对应于熵流和负熵流,若是负熵流,则导致dS大于零、等于零或小于零的不同结果,即系统的熵可能增大、不变或减小。
由熵概念自然会引申到“负熵”,玻耳兹曼本人已经意识及此,而更明确地阐述负熵者,乃是薛定谔(量子力学的创始人之一)。
他把玻耳兹曼的定义式(5)反其意而用之,便有
- S= kloge1/W (7)
若把W看作系统的无序度,1/W便可作为其有序度,那末这“取负号的熵,本身就是有序的一种量度”。
达尔文创立的(生物)进化论与热力学的构建和发展,恰是19世纪两大同时并重的科学建树。平衡态热力学视孤立系统乃沿着熵增的方向演化而抵达平衡态。进化论提供了生物界从低级向高级进化的美妙图像;薛定谔把熵概念推广用于生命物质系统及其进化过程,就使这幅美妙图像更为简洁、更为理性。原来,生命过程与负熵联系着;负熵、以至熵减,是导致生物进化的一个必要条件。薛定谔在《生命是什么》一书中说得很清楚:“生命似乎是物质的有秩序和有规律的行为,它不是完全以其从有序转向无序的倾向为基础的,而是部分地基于那种被保持着t的现存秩序。” 这“现存秩序”即体现于负熵,或说是低熵态。其实,生命有机体就是“依赖负熵为生的”;它不是孤立系统,在向外界吸收低熵态(有序度高)的养料、排洩高熵态(有序度低)的废物的过程中“不断地汲取负熵”,从而促使自身新陈代谢、生长发育、摆脱死亡、维持生命。负熵既为有序的量度,必然是“十分积极的东西”;而“新陈代谢中本质的东西,乃是使有机体成功地消除当其自身活着的时候不得不产生的全部的熵”。对照(6)式而言,生命有机体自身的熵增diS>0,从外界汲取负熵流,即deS<0,且|deS|≥|diS|,则有机体得以健全地生存,负熵流是在抵偿着自身的熵增;及至不再有负熵流进入,S达到极大值,生命过程便终止。至于生物界从低级向高级进化,有序度升高,不同发展阶段的生命物质系统的平均熵降低。
所以说,负熵是开放系统从无序向有序的进化过程的“时间之矢”,上面以生命运动形式说明了这个问题;当然, 进化过程更是不可逆的。熵增使孤立系统从非平衡态演化到平衡态,熵减则往往使开放系统从一种非平衡态进化到另一种更高级的非平衡态;进化是有积极意义的演化。
平衡和非平衡
热力学的研究从平衡态转向非平衡态,竟然将物理学以至科学引人意想不到的奇异境地。非平衡态热力学的显著进展,可算得是20世纪后半期最有价值的科学成就之系统若偏离平衡态,一些表示系统“强度”的量、诸如温度、粒子密度(浓度)等不均匀,相应地它们的梯度不为零,从而导致热流、粒子(扩散)流产生;若将这些梯度定义为广义“力”,则由其便引起系统内的广义“流”。如果系统偏离平衡态不远,或日处于近平衡态区域,“力” 和“流”尚保持线性关系,那末熵产生为极小,并与负熵流相平衡,即dS= 0;由(6)式得知,从外界进入的负熵流(dSe<0),其|dSe|=|dSi|。此时温度等“强度”量虽处处不一,但这些量却联系于一种稳定(不随时间而变)的不均匀分布,表明系统尚处在稳定的非平衡态。既为开放系统,此非平衡定态必然伴有一定的耗散,比如与外界有热量或粒子数的交换;这种近平衡区内的物质和能量的耗散,保证了系统的dS= 0。
在平衡态或近平衡区的稳定态的附近,纵有微小的涨落,亦破坏不了系统的稳定性。但在远离平衡态的区域,微小的涨落会被放大,从而导致系统突变,进入截然不同的全新状态。这时,近平衡区定态所遵循的“最小熵产生原理”已不复存在,广义力与广义流之间的线性关系也不复存在。仍看(6)式,一旦外界输入的负熵流之|dSe|>|dSi|,以致dS< 0,系统就有可能走上愈益有序化的进程,或可形成特殊的时空结构;这种“自组织”结构往往以能量(和物质)耗散为代价,故称之为“耗散结构”。耗散结构只可能出现在开放系统的远离平衡区。
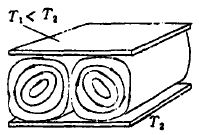
图11-2
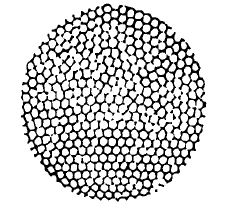
图11-3
且对普利高津及其布鲁塞尔学派的成员阐述耗散结构论时所列举的对流等现象作一粗略说明。平底容器里盛水,底部加热,水自下至上有温度梯度。设水的底层与表面层之间的温差为?T= T2- T1,它与一特征参量成正比。当?T增大、致使特征参量的取值达到其临界值时,会出现突变:水上下翻动、形成对流。对流元胞呈六角形;从上面看下去,像是一幅由无数六角形组成的对称图案(图11-3)。每个元胞里,水自下向上、再回旋着向下(图11-2)。就这样,水分子“自组织”起来,分子运动从原来的杂乱、无规突然转变成协调、规则而有序化了。对流是流体系统偏离平衡态甚远时所出现的一种典型运动形式、有序度明显的时空结构。而开放的化学系统在一定的条件下亦会出现有序结构,所谓的“化学钟”煞是好看、奇妙无比。管如说,已发现在某有机酸的特殊反应中,其组分(可能为铈离子)的浓度周期性地变化,造成反应液忽红忽蓝、忽红忽蓝地变,宛若钟摆一来一回地摆动。甚至还发现,在特定条件具备时某些反应液的浓度会突变成不均匀的特殊分布形式、以致呈现规则而漂亮的时空花样。“化学钟” 等效应也是化学反应过程进行到远离平衡区时才出现的。
由上述可见,孤立系统的熵增至极大值,便达到绝对的平衡,其熵变dS= dSi= 0,当然并无质能耗散相伴随。开放系统有耗散,在近平衡区dS=0,故处于稳定状态。开放系统在远离平衡区dS<0,形成耗散结构。至于静态的有序结构,例如晶体结构,是长久稳定的平衡结构。而有序的耗散结构起始于非平衡态,并依赖于负熵流、取决于特定条件,是一种动态结构;特定条件不具备,这有序亦就消失殆尽,所以这种结构与静态平衡结构不能相提并论。爱因斯坦也曾研究过热力学,导出了平衡态附近的涨落几率与涨落所引起的熵变之间的关系公式,由以表明随着熵增大,平均涨落会被衰减掉,因此系统不受涨落影响而依然趋近于、稳定在平衡态。上 面述及在远离平衡态,系统由非平衡态突变而形成耗散结构,却正是涨落不衰减、其影响反倒放大所使然。那末,可认为普利高津等人发展了爱因斯坦的热力学涨落理论。所谓“非平衡乃有序之源”这一说法,还是比较恰当的。
耗散结构的奇异美
耗散结构最奇异,也似乎最不可思议的一点,兴许在于:与它联系起来的那种远离平衡区的热力学系统之不可逆演化过程,竟然起因于系统的动力学行为及其动力学机制,对此并可用明确的动力学方程予以描述。但该方程是非线性的,这与描述可逆的动力学过程的线性方程甚有差别。差别之一,非线性方程对于初始条件极为敏感,初始值若有了微小变化,方程所给出的某变量的变化轨迹便偏移甚大、甚至会面目全非。换言之,初始涨落会被非线性动力学机制放大许多,并带有很大的随机性。

图11-4

图11-5
图11-4表示一个叉式分岔。图中X为热力学系统的一个“强度”量(例如浓度),它是特征参量λ的函数。λ= 0对应于平衡态。λ的临界值为λc。当λ<λc时,系统处在线性非平衡区,尚还稳定;当λ≥λc时,系统进入远离平衡态的非线性非平衡区。然而从λ=λc起,系统之状态变化所满足的非线性方程的解出现分岔,即代表原先解的一个热力学分支失稳,同时出现一对颇为对称的稳定解,二解对应于分岔后的两个分支b1和b2。远离平衡区里的涨落对系统的演化至关重要,非线性动力学机制使涨落放大,导致系统随机地选择b1分支或b2分支;当λ超越了λc,非线性动力学机制对涨落却有抑制作用,从而使系统稳定在所选挥的分支上,其状态已发生突变,形成稳定的耗散结构。继而b1分支和b2分支还会分岔,图11-5便是逐级分岔图。随着λ值渐次增大,系统离其平衡态越来越远,分支解一级级地分岔,系统也就一次次随机地选择不同的分支。伴随发生的一次次状态之突变亦便呈现明显的随机性。非线性方程的解出现逐级分岔是常有的,而且一再分岔之后、最终会趋于混沌;整个过程中出现多少个分叉,实难以计数。容易明白,非线性动力学过程不会是可逆的,它具有线性动力学过程的决定性,又受著对于线性过程无关紧要、甚或并不呈现的随机因素的显著影响。普利高津料定:远离平衡条件下因自组织而形成耗散结构,乃由“偶然性与必然性、涨落与决定论法则的一种微妙的相互作用”所引起;在上面的逐级分岔过程中,“在某个分岔 附近,涨落或随机因素起着重要作用,而在从一个分叉到后一个分叉之间,决定论的方面处于支配地位。”当然,这逐级分岔过程不可能逆转。
在远离平衡区,广义力与广义流之间的关系十分复杂,不同的力和流之间有相互影响,系统之不同元素亦就因彼此间的相干作用而产生协调动作,形成时间上、空间上或时-空上的有序化结构。这种有序化结构只发生在有耗散的开放系统里,有赖于负熵流的存在、有赖于非线性动力学机制所导致的正负反馈作用。例如激光与自然光相比不仅是强光,更本质的特征在于它是相干光、因非线性发光机制、因相干效应而产生,其高单色性、高定向性、高光子简并度正是其高度有序的表现。相干效应引起自协调、自组织。 生命恰是自协调、自组织和最高杰作。生命有机体可谓多层次的耗散结构。当然,一般的耗散结构都是多元素、多因素、多层次的复杂系统。
从耗散结构的起因、形成条件以及特征、描述方式等方面来看,它与作为物理学主体理论所研究的“哈密顿系统”[参阅“美哉物理”(九)]相比,甚有区别,亦就甚有奇异之美;且从这个角度,将本文作一小结。首先,耗散结构把两个意思颇远、甚至有点儿相悖的概念:耗散和有序的凝敛统一起来;当然,耗散是形成有序结构的条件之一。第二,开放系统的熵减使其走向有序,耗散结构依赖负熵流维持;这种由有序化导致的时空结构呈动态的稳定,是系统之演化过程中某一阶段的稳定形态,此乃远离平衡区里的相对稳定,与线性动力学系统的稳定轨道或孤立的热力学系统之平衡态的绝对稳定大相径庭。第三,熵增是孤立系统自发演化过程的标志,熵臧是开放系统有序化演化过程的标志;也就是所谓熵是系统之不可逆演化的时间之矢。耗散结构作为有序化的结果,表明熵减过程更具积极意义,导致系统进化,即朝着t从简单到复杂、从低级到高级的方向发展,故而负熵是进化之矢。至于生命,是宇宙中进化过程的局部结晶,是自然发展史上的进化顶峰,又可算得是耗散结构的最佳范例。第四,孤立系统自发地趋于平衡态,乃是纯粹的热力学过程;然而,对开放系统在一定条件下经由自组织、形成耗散结构的过程,却应溯源于热力学系统内蕴的非线性动力学机制,所以对于这样的过程必须予以非平衡态热力学和非线性动力学两方面的描述。这两种描述方式是互补的,二者恰可在耗散结构上得到统一。第五,导致耗散结构的非线性动力学机制,集决定性和随机性、偶然性和必然性于一体。大凡具有这样相反相成特征的系统必定很不简单,非线性动力学则披露了物质世界的复杂性。
耗散结构的形成需要若干条件(前述λ>λc就是一个主要条件),同时又往往因涨落不同这偶然性而形成炯然相异的有序结构。物质世界的多样性亦盖出于此。
耗散结构的奇异之美,则体现于上述相悖概念、相反特征、相左起因以及相违的描述方式的互补和统一之中;这种奇异美联系着大自然之非线性、复杂性、随机性和物质及其运动方式的多样性,当然比迄今物理学之主体理论的美学旨意更为丰富、多彩、玄妙、朦胧,尚待挖掘、细察、探讨、深究。
因此可以说,耗散结构论架起了从平衡态热力学到非平衡态热力学、从线性动力学到非线性动力学、从线性物理学到非线性物理学、从线性科学到非线性科学的桥梁之一。它有助于热力学与动力学的协调以及物理学之涵容的扩充,特别是促使熵和负熵概念向化学、生物学、信息论等领域全面地渗透;而随机性、复杂性、非线性、演化乃至进化等,将成为物理学未来发展的重要方面。恩格斯说过:“整个伟大的发展过程是在相互作用的形式中进行的”。实际上物质的相互作用非常复杂,由其造成自然界变化无穷之复杂而伟大的发展过程。那末,物理学今后终究要受到更复杂、更伟大的挑战。耗散结构论、信息论、现代生命科学、一般非线性科学等新款学科的兴起,是人与自然之新对话的开始,从而打开了展望科学未来的窗口;从这窗口看出去,乃是一片更奇异、更灿烂的,不断进化、生气勃勃的新天地。
____________________
*现正临近普利高津逝世(2003年5月28日)一周年。本文阐述其非凡的科学思想,谨以此作为对这位杰出的科学家、思想家的纪念。
*玻耳兹曼论证了S与logw的正比关系,普朗克将此关系写作等式。当然,人们都承认玻耳兹曼是该式的发明者。式(5)中的log当为loge, 亦即ln。