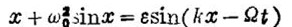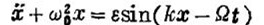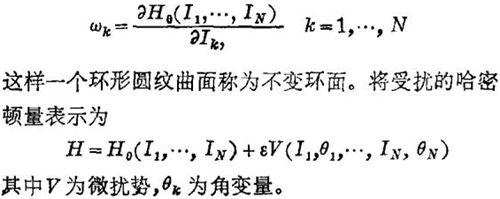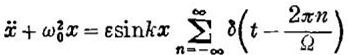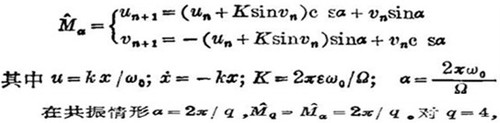40年前A. 爱因斯坦给M. 玻恩的一封信中写道，“上帝不玩骰子。”爱因斯坦是始终反对量子论的概率解释的、他不倦地探索着与经典力学更为直接的类比，即考虑没有概率不定性的确定过程。

如今，40年过去了，没有人会惊讶：甚至在一个经典哈密顿动力系统中也存在着浑沌（chaos）！在物理客体规则运动的领域内，在没有人预期会有的地方冒出了统计规律，使一个看来陈旧的课题重又振兴起来获得了新生命，造出了一幅不平常的物理动力学图画。

动态浑沌（dynamical chaos）是在一个决定性动力系统中，即在一个没有无规扰乱的系统内显现的表观不规则运动。物理系统内浑沌的发现引起了对自然规律的新认识。即使对非常简单的物理系统来说这类浑沌也是不可避免的；另一方面，由于在下的规则运动的对称性在浑沌内部存在着意外的有序。

从规则运动转变为紊乱的随机运动不是一件陌生的事。流体中的湍流运动，起初是规则的层流，随着流速增加而后就发生这样的变化。这曾被认为是和甚大自由度数的相互作用相关的。但是很出乎意料，对于只有少数自由度的体系也有浑沌动力特性的可能。

局域不稳定性与搅拌（mixing）

局域不稳定性的概念是了解浑沌现象的基础。由系统的坐标与动量构成一个相空间，系统的状态就由相空间内的一点来表示。相空间一定的体积内所有可能的始态集合可被描写为相空间内的一个小滴，称为‘相滴’。系统状态随时间的变化就相当于‘相滴’在相空间内的运动。根据刘维定理，对于保守系统，在‘相滴’的演化和形变中它的体积保持不变。若‘相滴’的形状变化不大，则对应于系统的稳定动力学。‘相滴’形状也可能剧变；当彼此紧靠的相点在相空间内一下子散开时就出现这种情况。‘相滴’迅速丧失掉它的规则形状而获得的是一个伤疤般的边界。这就是系统局域不稳定性的一个表现形式。

如果把相滴以外的相空间想象为涂成另一种颜色的液体，那么局域不稳定性就会引起这两种液体的迅速搅拌。搅拌的结果，在相滴所占的区域内夹杂着大量“泡沫”。随着相滴散开它所占的容积越来越大，造成一些越来越细的丝。

局域不稳定性引起物理体系轨道的搅拌。那么，动力系统的什么特性使得它们孕育着浑沌的可能性呢？

随机层

一个受到周期性外力扰乱的摆可供我们研究浑沌发动的许多特征。这是一个普通的物理模型，它的运动方程为

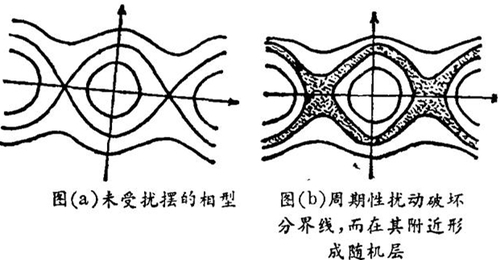
其中ω₀为振动的角频率，ε为扰动的参数，而扰动的空间与时间周期分别为2π/R和2π/Q。当摆为自由时，即没有外界的扰乱（ε=0）时，在摆的相平面上有清晰的轨线，它们通过单摆不稳定的上平衡态，后者在相平面中对应的点称为鞍点。这些轨线合成一串相似的橄榄形环（如图（a）），它们把相平面上不同类型（振动与旋转）的相迹分隔开来，所以称为分隔轨线或分界线（separatrix）。它们则既不对应于摆的振动也不对应于摆的旋转。因此，邻接分界线的相空间区域对任何扰动，即使是非常微弱的，都特别灵敏。

周期性扰动（本例中的εsin（kx－Ωt）代表一个沿x轴以速率Ω/k传播的平面波）破坏了这个分界线，在其ε邻域形成一个随机层（如图（b））。在此层内运动是浑沌的。在随机层所占的区域有一些随机轨线不能进入的孔（holes）。随着ε→0，随机层的厚度也渐趋于0。

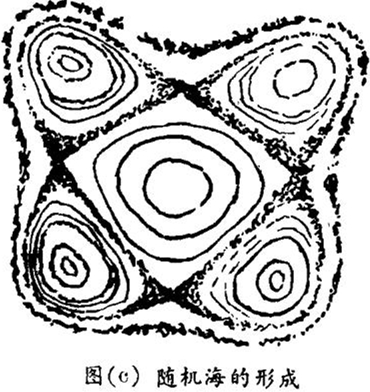
随机层的存在是哈密顿体系的一个普遍特性。典型的来说，相空间内存在着许多分界线。它们将相空间分隔成不同大小的区域。外界的扰乱或不同自由度的相互作用破坏了未受扰时的分界线或将所有分界线包在一个随机层内。它们可以合并成一些大的随机动力学区域，视层的厚度和它们在相空间内的位置而定，产生一个随机海（如图（C））因此，可以把随机层看作哈密顿体系中的一颗浑沌种子 · 在海内有大量浑沌轨线不能贯穿的稳定岛。在一个岛内有准周期运动区和俘获浑沌区。浑沌愈强岛就愈小而被随机海占去的相空间部分就愈大。

我们尚未提到浑沌发动的所有特性，然而我们已经明白，我们遇到了一组特别复杂的现象。

弱浑沌与间歌现象（intermittency）

具有浑沌动力特性的系统一般含有稳定岛，岛边界附近的运动未必与“最近”的规则轨线所描述的运动有很大的差异。浑沌愈弱，稳定岛的面积愈大。间歇现象是弱浑沌的表现形式之一，这个概念是从湍流理论借来的，那里用在一个耗散动力系统中。然而在哈密顿动力学中，间歇现象有另外一些特殊的特征。

考虑一个线性振子的方程：

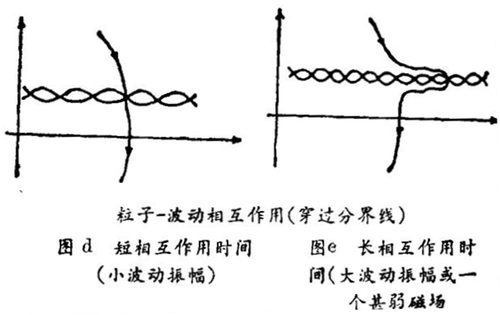
它也可以用来描写在一个沿着z - 轴指向的磁场再加上一个沿x轴传播的平面静电波场内一个带电粒子的运动。此时ω₀为迴旋频率。这个方程的问题包含了浑沌的多方面模型，研究起来不是那么容易的、最先是联系等离子体中离子的随机加热来研究的，在相平面上，在磁场内的圆运动轨道穿过平面波的分界线（图（d））。这两类运动在分界线附近强烈地相互作用，有两种极限情形是可能的。可以把每次穿过分界线看作是改变一个粒子的能量和相位的一次“碰撞”。可以证明，若发生了强浑沌，且若满足条件则碰撞时间与迴旋周期相比是短的（图（d））。

在弱磁场（ω₀→d）中则粒子在穿过磁场的过程中将在分界线附近完成多次振荡（图（e））。这时，碰撞的时间非常长，这就导致粒子具有浑沌的动力学特性，但是显然能量和相位的变化是小的。因此，只有长期积累的变化才能造成轨线的局域不稳定性。从而，这也意味着粒子的轨迹将由不时稍有修正的长的规则线段所组成。这种状况举例说明了哈密顿间歇现象。然而，这并非包揽了弱浑沌的所有特性。间歇现象和电子在固体中的所谓Anderson局域化之间的内在联系会导来凝聚态物理中新的有趣结果。

KAM定理

KAM定理，即由Kolmogorov，V. Arnol'd和J. Maser产生的定理。它的基本内容是和有弱扰动的情况下哈密顿体系的独立运动积分的守恒问题相关的。假定未受扰动的系统具有N个自由度，是可积的并且由哈密顿量H₀（I₁，…，I_N）描写。可以将这些作用量I_k选为N个独立的运动积分（不变量）。在此情况下系统的轨线是条件周期的。它绕在一个N维环面上并且由N个角频来表征

KAM定理的基本结果是，对于微弱的扰动（小的ε）而言，上式所描述的系统的环面虽然有些畸变，但系统的不变环面的大部分还是保存的。这个陈述证明，存在着一些永久稳定的区，在这些区域内浑沌是不可能的。然而也存在着定理的假设失效的一些区域，在那里是可以期望出现浑沌的。数值实验证实了这些预料。在ε＜1的弱微扰情况下，KAM定理失效的那些区域被证明就是前面讨论过的随机层。随着ε增大、因冒出邻接的随机层，它们之间的距离消失而使随机层的厚度增加。对某一定值ε_c，层迭加起来而合并成一个大的随机海。B. Chirik v在1959年提出了这类重迭的条件并作为出现浑沌的一个条件。

随机网（stochastic web）和Arnol'd扩散

一般情况，相平面上岛和随机层的图案可能意外地复杂。1964年Arnol'd注意到自由度数N超过2的系统有下述特性：在零级近似（ε=0）下，系统的分界线相交造成一张覆盖全部相空间的复杂网络。对于任何有限的ε，这些分界线或者被消灭，或者被包在薄的随机层内。尽管随机层薄，粒子却可以沿着由这些层构成的互相连通的网络通道游荡。这个非常重要的现象被称为Arnol'd扩散。它描述了几乎所有N＞2的物理系统的一个万有的不稳定性。

在受扰哈密顿量的表式中，我们已经了解到H₀产生覆盖相空间的分界线网络，而对任意小的ε，微扰εV产生具有随机动力特性的通道而使其破坏。我们将这种在任意弱扰动下遍及整个相空间的全局性游荡（global wandering）称为“最小浑沌”（minimal chaos），而通道网络就是我们所谓的“随机网”。（stochastic web）。Arnol'd最先估算了沿此网扩散游荡的速率。

全局性游荡导致一个极其重要的物理现象。在网的通道内部运动的粒子的绝热不变量可以一直变化到它们任意地强。这意味着总有与网的覆盖区大小正比的一部分粒子，它们的动力学特性是始终不稳定的。

最重要的问题之一是：有最小浑沌可能的最低维数是什么？Arnol'd不等式N＞2是否为一极限不等式？换句话说，对于N≤2是否存在无限大的随机网？这些问题的回答只是最近才得到，放在下面讨论。

最小随机网

我们早就指出KAM定理只在某些条件下才有效。一是在未受扰的系统中没有简并。这意味着：

det|?²H₀/?I_j?I_k|≠0                         条件1

这个条件意即系统H₀是非线性的。当去掉这个限制时，状况改变了并且在N=3/2时随机网就已有可能了。这就是最小的维数，因为对N=1动力系统是可积的并且浑沌是不可能的。

现在再回到描写带电粒子在一恒定磁场及垂直磁场传播的平面波场内运动的方程。简并是在共振条件

qω₀=Ω                               条件2

下产生的，其中q为一整数。

在此情形下的相型有一蛛网状的分界线网络及网眼内的不变曲线的轮廓。分界线为指数减薄的随机层所覆盖。对任意小的ε都存在这网，并且粒子可以沿着它的通道毫无限制地游荡，这意味着粒子能量无限地增长。在实际情况下，对于小的粒子的扩散行进距离受到限制，这是因为网的通道随着范围的扩大而变得愈来愈窄，使得在其内部的扩散也愈来愈弱。

当条件1成立时，网被破坏，但它的结构可以部分保存。在前述的受扰摆（非线性振子）的例子中就有这种情况。摆的振荡频率由于它的非线性而不再是ω₀。因此，即使在共振条件（条件2）下某些分界线的交织消失并且辐向运动变得不可能。只有随机层的有限厚度能够帮助克服这个困难。这样的网有一部分被镶在摆分界线的元胞中心去了，并在那里产生一个既有规则的也含浑沌成分的结构。两例都表明，在弱扰动下不管是确切的简并还是接近这种状态都导致定域在具有明显结构区域内的弱浑沌的发生。

而且，当撤去微扰时这些结构消失，它们只是由于微扰的存在才出现的，并且它们总有一个随机网。

具有晶体对称性的随机网

当未受扰时的运动频率ω₀与扰动频率Ω之间满足共振条件（条件2）时非线性起着不平常的作用。非线性可以使系统迅速脱离共振而稳定下来。这一事实说明了KAM定理中的条件1所起的特殊作用。不满足这个条件时，可以预料通往浑沌的道路性质上要更换。一个粒子在一稳定磁场和垂直此场传播的一个宽波包的复合场中的运动可由方程

描写。方程右侧的力包含无限多模式。它描写一个“被抖动的”振子（a“kicked” oscillator），抖动的周期为2π/Ω。

方程包含具有两类对称性的力场。ω₀²x项产生相平面上轨线的旋转对称性而扰动相对于变换x→x+2πn/k（其中n为一整数）具有平移对称性。在共振条件（条件1）下即使对小ε这些对称性的相互作用也是强的。何者将幸存下来？在2 - 维情形中这两类对称性，旋转和平移的并存只有在特殊情况下：{q_c｝是集{1，2，3，4，6｝时才可能。q值不属此集时会发生什么呢？

运动方程也可表示成差分式：

相平面为一无限大的、形状接近一个正方晶格的随机网所覆盖。网厚为exp（－常数/ε）量级且对任何ε都存在。对q=3和q=6，网成六方晶格形。

然而对q的其它所有值（q≠1，2，3，4，6），形成一个具有所谓准晶型对称性的非周期网络。这种由一个随机轨线产生一个复杂规则结构的极为有趣的事实是和最小浑沌的问题密切相关的。

经过对网的几何特性的复杂分析，我们能够找出在旋转与平移之间的竞争中那一类对称性能胜。在这类竞争中浑沌的出现是一个普遍特性，这决非偶然。弱浑沌是矛盾的对称性之间的一个折衷。

随机网都是分形的（fractal）。网的规则图案可以由它的付氏谱（Fourier spectrum）来展现。这表明，我们在此遇到一种新型的有序，它的研究将有助于了解物质自组织的新形式。

实在的准晶体已经获得并且已经证明准对称的流体力学体系可以存在。对这些结构的新探索是和随机网的特性联系一起的。

浑沌愈弱，也就是网越薄，结构就越规则。最小浑沌产生准对称的结构。

留待解决的问题

对于最低可能维数的物理体系，随机网的存在表明了随机的和规则的动力学特性有着何等牢固的联系。了解这类联系对物理学的许多问题，诸如稳定性，从层流到湍流运动的转变，凝聚物质中图形的出现，带电粒子的随机加速等等，都是重要的。

由研究动态浑沌的特性，我们发现了自然规律的新方面。力学和电动力学的方程可以描写规则的和随机的运动。关于这可以如何发生现在有了颇为详尽的知识。然而，随机的和决定性方面的综合是非常复杂的，很多有关问题有待于解决。将这些观念应用于量子论还不过刚蹒跚了几步。

实在的浑沌原来并非在相空间内全部搅浑。浑沌区与镶嵌在浑沌区内部的那些区域共存，造成一幅有序和无序相间的异常图画。实在的浑沌真是这样的结构吗？

[Physics Today，1988年No. 11]