恰在一年多前的一个晚上,当旧金山人正安享棒球赛事之乐时,却几经遭受了令人恐惧的震击。就总体地域而言,那次地震并非完全不可预料,但是肯定没能极精确地测定准确的日期和位置,尽管人们为了理解地震的复杂而潜在的动力学原理而作了坚毅的努力,仍然无法准确预报它们。
现在应将地震理解为分形现象还是混沌现象,一些分析人员尚不知晓究竟哪个更好。他们正在找寻一些相当简单,且有时对称的模型,以便揭示那些极复杂、不对称和混沌的行为,假若模型被证明能准确描述断层带上地壳的真实运动,那么它们可能有助于确定重要参数或者透彻了解重现模式。反过来,如果像有些模型描绘的那样,地震表现出决定论的混沌行为,解的指数发散将阻碍长期的预测,尽管利用方程式可以毫不费力地作出短期预报。
分形结构
“分形”一词是曼德尔布罗特(Benoit Mandelbrot)于1982年创制的,借以描述许多不同尺度上某些现象的空间模式的相似性,在这以前地质学家已认识到,地震带具有与分形有关的某些特性。加州理工学院的古登堡(Beno Gutenberg)和里克特(Charles Richter),在四十年代初已注意到,大于某个给定震级m的地震发生的频度f(m),可由下列公式给出:log10f(m)=c-bm(式中b、c为常数)由于震级依次与矩的对数有关,所以上述关系实质上符合幂律。大小变化在10的数次方的范围内的所有震级,这个规律均有效,对世界性的断层带斜率b都接近1。这个关系表明:小事件与大事件一样遵循同一规律,即意味着所打的事件必定服从一个尺度不变性机制。这就是分形行为的精髓。地震的震级与区域有关,因此由古登堡 - 里克特定律所暗示的自相似性也与空间尺寸有关。
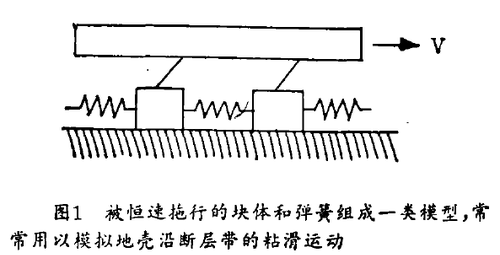
这样,分析人员已经明确断层带遵循分形统计,但他们不知道其原因。去年,加州大学圣巴巴拉分校的卡尔森(Jean Carlson)知分校理论物理研究所的朗格(James Langer),他们利用简单的块体 - 弹簧模型(block-and spring model)重现的行为近似于震级与频度的古登堡 - 里克特关系式、他们的模型的基础是伦敦施卢姆贝格尔 - 道尔研究所的伯里治(Robert Burridge)和加州大学洛杉矶分校的诺朴夫(Leon Knopoff)在1967年首先设计的模型,据此来描述地壳沿断层带的粘附和滑动。块体由弹簧互相连结,同时依靠其他弹簧,块体链被驱使着恒速运动(见图1)。当块体受驱拉时,起先粘附着,一旦弹簧力大于静摩擦力,那么一个或多个块体即刻全部滑动,直到弹簧力减缓下来为止。伯里治和诺朴夫对块体链的物理和计算机模型都作了研究。由于计算机功能的局限,那时仅限于10个块体。利弗莫尔劳伦斯实验室的伦德尔(John Rundle)告诉我们,他们及其余早期的研究者已经发现了幂律性状的一些证据。
卡尔森和朗格利用一大批耦合微分方程来描述块体链,将它扩展到200块之多。在卡尔森和朗格的模型中,随着块体速度的增大,摩擦力减小。非线性特征遏止了静摩擦与动摩擦之间的突变。一旦系统达到统计学的稳定状态,卡尔森和朗格将每个块体的速度作为时间函数记录下来。在小事件中仅有单个块体以低速滑行,散布于小事件间的大事件就涉及许多块体,并且它们的速度超过块体链被拖行的速度。偶而所有块体同时滑动时,灾难性的事件发生了。圣巴巴拉的科学家注意到,小事件只有一个或几个块体在仍然固定着的其他块体之间滑动,而它们有使块体间距相等的趋向,因此对系统有“平缓”作用。结果,一大组块体下回可能一起滑动,就这样“平缓”为更大的牢件辅平了道路。又由于移动得较快的块体所受的摩擦力较小,一组滑动着的块体间的任何不均匀性将得到扩大,因此较小的事件不断地产生。
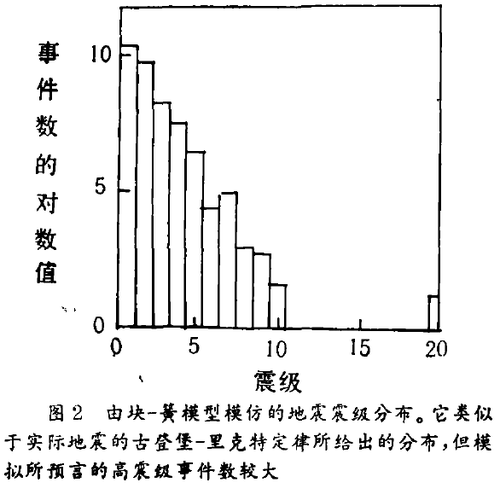
为简化不同规模的事件的统计,卡尔森和朗格对每个事件定义了“震矩”(moment),它是对块体总数和它们的位移两者的量度;又定义了“震级”(magni-tude),它是籐矩的对数。在对数坐标图上,震级的直方图显示出事件数遵循古登堡 - 里克特型的幂律,且斜率约等于1。(见图2)对于高籐级的事件,出现了对古登堡 - 里克特定律的显著偏离:块体系统经历的滑动比简单公式所表明的更大。
卡尔森告诉我们,像他们那样的简单模型有助于地越发生的重要参数的识别,也能为估计重现次数的规律提供导向。然而,她指出,模型是对断层过程的简化,而个别地震的关系仍是繁琐的。
自组织临界
卡尔森和朗格注意到,他们的地震模型是“自组织临界”之一例,此概念是布鲁克海文实验室的巴克(Per Bak)、现在加州圣巴巴拉分校的唐超(Chao Tang)和佐治亚理工学院的维森费尔德(Kurt Wiesenfeld)于1987年提出的。巴克和他的同事们确实常常将地震引作自组织临界的例证。按照他们的概念,某系统处于边界稳态,因扰动而偏离平衡时,系统会自然地演变回边界稳态。换句话说,这样的系统组织自身永久地处于临界状态。这三位理论家认为,自组织临界的机制可能是功率谱呈现“1/f”噪声的所有系统的基础。这些系统在一个很大的频率范围内与f-β成比例,而β接近1。由古登堡 - 里克特识别的幂律表明地震属于这个范畴。
作为自组织临界的一个例子,让我们看看一个沙堆吧。假若沙堆是如此陡峭以至于附加一颗沙粒就将导致整个沙堆的崩坍,那么这个系统是不可能抵抗微小的扰动而保持稳定的。倾斜度小的沙堆更为稳定:外加沙粒可能仅仅诱导小的滑动。组成沙堆的许多区域中虽然也有扰动的传播,但是这些区域彼此互不通达,因此滑动不会无限地扩展。如果我们缓慢地增加沙粒以构建沙堆,它既不会达到陡峭不稳的状态,也不会由于小“坍方”而达到浅薄状态,但是最终它将演变为临界状态,而它有别于那种所有各种规模的坍方都可能发生的极端极态。处于临界状态时,沙堆保持在同一平均高度,因为新加入的沙粒被不同规模的偶发坍落所抵消了。巴克、唐和维森费尔德断言,对这个系统不再存在自然的长度标尺。坍方规模的起伏与系统功率输出的涨落相一致。
巴克、唐和维森费尔德,以及后来芝加哥大学的卡丹诺夫(Leo Kadanoff)、内格尔(Sidney Nagel)周素敏(Su-Min Zhou)和吴磊(Lei Wu),利用分格自动机模型将“坍方”研究置于定量的基础上。在那个模型中,网格及它与邻近网格的相互作用由简单的规则支配,这些规则利用公式去模拟沙粒空间排列的性状。每个网格的状态给予一个整数值,它表示沙堆该处的局部斜率。当向沙堆加上1粒沙子时,可简单地在随机选择的网格上加一个整数。假若总和超过了某个临界值,它就减小确定的总数,比方说4,而每个邻近网格计数增加1。因此,如果某个给定区域内的许多网格接近临界值,扰动会触发牵涉许多沙粒的坍方。巴克和他的同事们从随机分布的斜率开始每一次模项试验,然后周期性地将沙粒加到随机网格上,每隔一定操作时间,他们就检查邻近沙粒激发的坍方程度,即受扰动影响的网格数,他们发现了作为群体数量和时间尺度的函数的事件的幂律分布。
假若以每个网格的整数表示弹簧力的强度,而阀值是最大静摩擦力,那么关于坍方的分格自动机模型恰能容易地模拟由弹簧连结的块体陈列的性状。事实上,巴克和唐将这个模型应用于二、三维陈列中的8000个块体来研究地震的自组织临界,他们发现以一定能量释放的事件的分布与E-r成比例。他们没观察到大幅度的偏差。巴克觉得,定标行为可以解释为何无法很好地预报大地震,但是他们更怀希望地注意到,这也表明人们可以通过研究小地震模式以推论有关大地叔的信息(这类信息的真实数据是稀有的)。巴克觉得,地震或处于临界状态的其他系统刚刚在混沌的边界上,因此长期预报被排除的可能性,就不像如果系统确是混沌的那么大。
一个类似的地震模型是由桑迪亚实验室的布朗(Stephen Brown)、哥伦比亚大学拉蒙特 - 多尔蒂地质观测台的舍尔茨(Christopher Scholz)和伦德尔创造的。当巴克和唐仅着眼于远离边界的模型样本时,布朗、伦德尔和舍尔茨检验了有限边界的效应。像卡尔森和朗格一样,他们发现大事件发生的频率要多于人们归纳小事件推得的结论。舍尔茨注意到,地震发生于地壳相对地比较浅薄的地区。地震学家早就觉察到,小到无法达到界区边缘的那些小地震与约束在这个尺度内的那些大地震之间的差别,因此,一定存在着冲破这两类地震间的定标的特征长度。
混沌
至今讲述刹的模型包含了一大群块体,而有人已在探索仅有几个块体的动力学机制。康奈尔大学的瑞绅(Andy Ruina)和其他研究人员已将从属于实际摩擦力的单个块#模型模拟地震,摩擦力取决于块体的速度和它的运动历程(所谓的速度和状态可变摩擦)。在瑞纳的模型中,摩擦力的参数化很大程度上基于加利福尼亚门洛伯克美国地质调查局的狄特里希(Janes Dieterich)的实验测量。与通用电气公司的纽斯鲍姆(Jeffrey Nussbaum)一起,1987年瑞纳决定探索尽可能简单的模型的结果,观察动力学能否单独产生空间不对称行为,而并非由断层不均匀性所致,回答是肯定的,纽斯鲍姆和瑞纳的模型由隶属于同一摩擦力的两个相同块体组成,随着块体的滑动和粘着,这个摩擦力在动态和静态的两个可能值之间变更。他们发现块体的运动是周期性的,然而一般不对称:在某些解中,一个块体总比另一个滑动得快些,而在其他的模式中两个块体交替地经历短暂滑动。
瑞纳和西北大学的霍罗维茨(Frank Horowitz)在新近的论文中分析了物质特性均匀的、且不受块体链末端的影响的带有速度和状态可变摩擦的模型,这实质上是一个沿断层不断变化着的滑动连续区模型。他们再次发现,动力学会产生地震现象的时间和空间的复杂性。
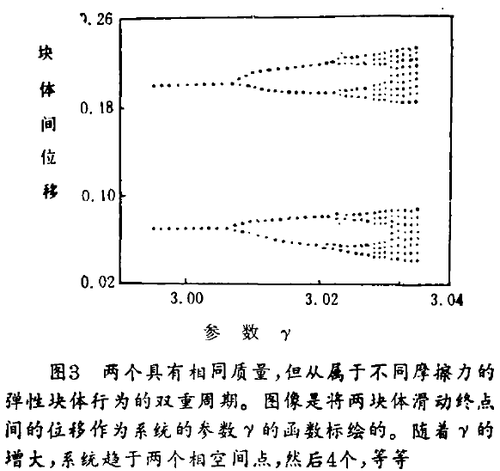
1990年,黄捷(Jie Huang)和图科特(Donald Turcotte)采用实质上和纽斯鲍姆、瑞纳同样的模型,但是允许作用在一个块体上的摩擦力大于另一个(比例系数为β),利用这个不对称性,黄和图科特获得了决定论的混沌行为的证据。他们分析时,首先显示系统在相空间的连续状态,并图绘比较两块体的位置。展现的轨道绝非如人们期待的那样,定于某一个或有限数目的点上,如果系统接近稳态或周期性行为,而是充满了相空间图。而且,系统呈现沿着双重周期路线、趋于混沌的现象:随着描述摩擦随速度变化的参数γ的增大,系统先是演变成单一的相空间点;然后当参数继续增大时,系统在两个终态之间振荡;接着4个状态、再后8个,等等(见图3)。
图科特告诉我们,他们计算一个模型的李雅普诺夫指数的正值,在这个模型中摩擦随着块体运动的加快而变小。(李雅普诺夫指数是对相空间中系统中出发时彼此相当接近的两个点的指数发散率的量度,)此项工作显示的混沌现象,仅指两个块体的系统,而非对地壳中的断层和裂缝复杂得多的结构而言。仍然需要观察、研究的是:低位模型中的混沌行为是否意味着混沌也存在于高位的真实系统中。
(Physics Today,1990年11月)