物理学之美, 美在哪里？ 美在充实、美在可靠、美在对称、美在统一、美在简洁、美在和谐、美在造福人类。而物质世界及其物理学描述、乃至物理学的理论构建, 其美学特征主要在于对称、在于对称与对称破缺的辩证统一； 故对称亦可谓物理美之源、物理美之最。

本文拟对此作一多方面的、然而简略的讨论, 也可算是对前面诸文有关内容的粗浅总结。

物理现象中的对称性直观而明显, 物理定律所凭依的对称性普遍而内敛, 因此物理学的美既朴素又精深, 其理论构建既严整又华彩。李政道先生指出: “ 艺术和科学,都是对称与不对称的巧妙组合” ；物理学尤其如此。对称性是一个古老的概念, 人们考察了两千多年,直至20 世纪的现代物理学, 其中对对称与对称破缺的探讨, 依然是一个艰深的研究课题。或许在21世纪, 物理学家还得深入探讨下去； 当然, 现代物理学也就随之愈益完善、圆满、优美。

大自然 无穷的对称

茫茫宇宙, 对称无处不在、无穷无尽。行星及其卫星、恒星系、星系、星系团… …都沿着圆、椭圆、抛物线、双曲线（参见图9-7） 等各具不同对称形状的曲线轨道运行。圆锥曲线等曲线中圆的对称性最高, 曲面、立体中球面、球体的对称性最高； 果其然, 从宇观→宏观→微观的各个层面上, 诸如天体、生物细胞、构成一切物质的原子、原子核等, 甚至整个宇宙, 恰恰俱都近乎球形。诚然, 球形并非世间万物的唯一形态。在二维图形和三维立体中, 正多边形和正多面体的对称性亦相当高。

图10-1 柏拉图立体

柏拉图立体模型（ 图10 -1）——正四面体、正六面体、正八面体、正十二面体、正二十面体与不同大小的球面一一内接、外接, 相互套合, 曾被用来解释宇宙结构, 虽然与近、现代宇宙学给出的结构图像不相一致, 但因展示了三维世界的一些十分齐整的对称形态, 而仍然受今人所青睐。此模型里的一些立体构型,时而在矿石晶体中见到。晶体对称性远较柏拉图立体的对称性丰富, 有几十种之多。

图10-2 旋涡星系

图10-3 双锥螺

图1 0 -2 所示的旋涡星系, 有鲜明的旋转（ 转动） 对称性。图10 -3 所示的双锥螺, 其形状是由连续的旋转变换、纵向平移变换和横向伸缩变换三者结合所致。

这两个实例表明, 许多物质系统往往具有变换（转动变换、空间平移变换等）操作下的不变性；变换的形式多种多样, 变换不变性是最广泛、最普遍的正规对称性。圆、球、正多边形、正多面体都具有连续的或分立的转动变换不变性。至于常见的物-像关于镜面的对称（俗称左右对称）并非转动变换不变性所使然, 而是空间反射（ 空间坐标x , y , z→-x , -y, -z） 变换不变性的体现。同样, 时间平移不变性和时间反演（时间t→- t） 不变性也是经常见得到的对称形式。

图10-4 对称图案中的不对称

正如李政道所言, 对称与不对称的巧妙组合才更为美观, 单纯的对称有时会嫌其过分单调。图10-4 是一幅由正六边形组成的对称图案画, 图案上还覆盖了展翅飞凤和多种花卉； 这似乎使原来十分规则的对称形式有所缺损, 其实是愈加增色添彩, 尤显灵活秀丽。

图10-5 阴阳太极图

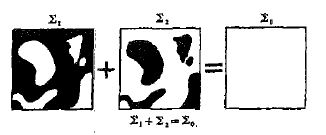
10-6 互补衍射屏

相反相成、互补并协, 亦是一种很基本、很普遍的对称性； 或可看作正规对称性的变型。粒子和反粒子、物质和反物质、黑洞和白洞、正电荷和负电荷、磁北极和磁南极； 微观物质体系的波动性和粒子性、连续性和分立（离散）性, 等等, 彼此间都是这种互补并协的对称关系。中国古代的阴阳太极图（ 图10-5）, 恰是这种对称性的绝妙写照。喻作阴、阳两极的黑鱼、白鱼, 除颜色不同外全都一样, 二者相互填补、拼合成一个具有最高对称性的圆； 此圆对于两条鱼而言, 还具有绕通过圆心之垂直轴的180º转动对称性（不管其颜色）。显然, 用太极图表示轻子偶素、夸克偶素（偶素者, 为正反粒子所构成）也是很适当的。而图1 0-6 是两个互补衍射屏。光通过二屏后在空间同一点所产生的衍射场之和, 等于光自由传播（ 即无屏） 时该点的光场； 那么, 两个衍射场互补, 表明两个屏的作用互补。互补并协的定义似可延拓。譬如说, 实物和辐射组成了整个物质世界, 亦即实物粒子——费米子（包括夸克和轻子,而夸克构成强子） 以及相互之间的作用场量子——（中间） 玻色子充满了全宇宙。因此, 费米子和玻色子是大自然的两类基本构成子, 二者互补并协、地位对等。

自相似性可谓物质系统在不同尺度、不同层次之间的对称性； 而同一层次上的相似性可算得是特定意义上的对称性。例如三代夸克-轻子（费米子） , 除质量外性质几乎雷同[参阅“ 美哉物理（四）”]。以质量不同而论, 这可看作各代之间的自相似性； 以物质结构层次而论, 三代夸克一轻子都属于同一“ 基底”粒子层次, 故对它们可予统一描述。那就是说, 不同粒子系统（一般而言, 乃不同物质系统） 的相似性, 正是其理论描述得以统一的依据。再如各种相互作用场的统一场论探索, 就是按照作用场（玻色子场）的相似征状（共性） 而去谋求其统一的场论研究工作。

对称性 物理定律之所倚

爱因斯坦最崇尚物理理论的对称与和谐； 他创建的相对论, 正是其对时空对称性予以成功研究的结果。关于这个事例, “ 美哉物理（七）”已有详尽的论述。’ 该文指出, 经典物理理论是时空模型理论, 故而时空对称是经典物理中最基本、最主要的对称形式, 由此对称性所支托起的相对性原理, 便是经典物理理论的逻辑前提。由相对论得知: 在四维时空空间里, 时间与空间坐标的地位对等。而一些物理量, 例如能量与动量的分量、电荷密度与电流密度的分量、电场强度的分量与磁感应强度的分量等等, 彼此间亦地位对等, 所表现出来的对称形式, 与时空对称均可比拟、甚至完全相同。在物质系统的两个惯性参考系之间, 时空变换即为洛仑兹变换, 物理量以洛仑兹张量表示； 如果参考系是非惯性的,对应之时空变换便是广义的非线性变换关系, 物理量以广义张量表示。当从一个参考系变换到另一参考系时, 时空发生变换, 以张量的时空微分方程表示的物理运动定律保持不变——张量方程形式不变、运动定律依然成立； 这就表明, 物质系统运动变化时, 乃受制于时空变换不变性。这种不变性, 与时空几何对称性不可分割, 前者依托于后者, 又是后者的具体表现, 故而前者又赋予后者以生动实在的盈盈风采。也就是说, 宏观物质世界千变万化的种种运动方式均凭藉时空对称性而遵循其确定不变的规律,经典物理所着力描绘的这种时空变换不变性（洛仑兹变换不变性或广义时空变换不变性） 是对称的一种高级形态。

对称变换的不变性, 往往与不变量相对应； 这种对应关系在物理学各领域普遍存在。著名的诺迪尔定理即指: 如果物理定律在某一对称变换下具有不变性, 则必定存在一个相应的守恒量。换言之, 在物理学中, 一种对称形式总是与一个守恒定律伴随着。例如三条基本定律: 能量守恒律、动量守恒律、角动量守恒律分别对应于时间均匀性、空间均匀性和空间的各向同性, 亦即物理定律之时间平移变换不变性、空间平移变换不变性和空间转动变换不变性； 此即时间、空间的三种基本对称形式。至于洛仑兹变换不变性, 比这三种基本对称形式的对称程度更高, 还反映了四维时空空间整体的转动变换不变性； 它与光速不变定律相关联。另外, 下文将说明时间反演不变性和空间反射不变性亦有不同的守律定律与之相对应。总之, 物理学里有许多运动定律都凭倚于时空对称性的方方面面； 而种种对称形式（不限于时空对称） 所对应的那些守恒定律则都是对运动定律有限制性意义的、并往往是物理学里的基本原理。

当然, 时空对称性是直观对称性； 除此之外, 物质系统还具有内禀对称性。特别是微观物质系统,探讨其内禀对称性, 亦就是研究其动力学性状和运动定律的量子本质。量子物质学家采用抽象数学方法, 将量子场的一些内禀性质看作抽象的内禀空间的对称性。且以同位旋说明之。例如, 核子系统的同位旋（是一种内禀量子数） 在强相互作用过程中是守恒的。核子—— 质子和中子的同位旋相同（ 但在一特定方向上的分量不一）, 二者被看作是同一种粒子、即核子的同位旋二重态, 可通过强作用（核力）而相互转化。转化过程中系统的同位旋保持不变。此守恒律对应于同位旋空间——一种抽象的内禀空间——的转动变换不变性； 这转动变换相当于核子在二重态之间转换, 即质子与中子互换。质子和中子在同位旋空间里的对等地位, 便可用以解释强作用（场）的电荷无关性。

直观的时空空间也好、抽象的内禀空间也好, 在其变换操作下的不变性都是几何对称性, 数学上均以对称群表示, 确是最简洁明了的。上面提到的种种变换操作分别构成时间平移变换群、空间平移变换群、（空间）转动变换群、洛仑兹群、反演（或反射）变换群等等。这几个对称群里除反演（或反射）群是二阶分立群外, 都是连续变换群,即属于李群之列。李群的生成元往往就是所对应的守恒量的一定倍数, 例如三维转动群SO（3） 的三个生成元即与角动量的三个分量成正比, 转动变换不变性便对应于角动量守恒。同位旋变换群是三参量的特殊幺正群SU（2）, 亦有三个生成元, 对应于满足守恒律的同位旋矢量。这些李群, 正是量子物理研究的最重要的数学工具。

凭借群论工具,“人们在对称性关系的研究中寻求前进的途径”（玻尔语） ； 说得更具体些, 人们为了发展量子物理学, 则须继承并超越爱因斯坦的研究方法: 着眼于变换, 使理论模型、运动方程“ 在越来越广泛的变换中具有不变性”（狄拉克语） , 从探讨时空空间的对称性转向对种种抽象的内禀空间之对称性的研究。上述同位旋空间是一例, 而最突出的成果是杨振宁和米尔斯所提出的规范场概念和规范变换不变性原理。当然, 这规范场理论的建树, 更离不开对群论工具的有效运用。

规范场, 更确切地应称作相位因子场。譬如说, 电磁场便是一种规范场, 可用单参量幺正群U （1）表示它在相位变换下的不变性, 与此相应的就是电荷守恒。相位因子为e^Qθ（Q是电荷、θ 是参数）, 作出相位变换后, 电磁场的运动定律保持不变。一般说来, 相位因子是局域性的, 即θ是时空坐标的函数。五十年之前, 杨振宁和米尔斯解决了同位旋变换的局域性问题, 并由以断定, 各种相互作用场都是局域场, 都满足规范变换不变性原理,只是场不同, 规范变换的形式也不同。显然, 由于此原理对所有量子化的作用场普遍适用, 便从而找到了使统一场论研究走向成功的捷径和通途。此原理是一条比时空变换不变性原理抽象得多、但涵义也更为深邃的对称性原理, 借助于它可反映量子场的共性, 并揭示量子场的深层次性状。对此, 杨振宁认为是“ 由对称性支配相互作用。杨先生等人的工作可谓吸取了爱因斯坦“凭倚于对称性而进行统一场论探索” 的方法之精髓, 又在研究深度以及工作成效上超越了他； 的确,规范变换不变性是一种比时空变换不变性更高级的对称形态。

简单说一下利用这规范原理统一相互作用的过程。现已基本完成的有两步: （一） 弱-电统一； （二）强-弱-电统一, 即“ 大统一”。用弱同位旋标志弱作用场的一种基本量子性状, 则相关的内享对称性亦由SU （2 ）群表示； 并将这弱作用场当作与电磁场地位对等的规范场。那么, 弱一电统一场总体的规范变换不变性便通直由SU （2） 群与表示电磁场之内桌对称性的U（1）群的直积表示, 即以SU （ 2 ） x U （ 1 ）作为弱相互作用偕同电磁相互作用的规范群。自然, 此直积群的对称性高于其子群SU （2 ） 和U （ 1 ）。它有四个生成元, 对应于弱同位旋守恒和电荷守恒, 还对应于四种“荷” , 即四种规范粒子: 传递弱作用的（ 弱） 中间玻色子W士, Zº 和传递电磁作用的光子γ[或可称作（电）中间玻色子]。

对夸克之间的强相互作用还得引入“色”这个内禀自由度（夸克有三“色”） ； 强作用场就是所谓“ 三维色空间” 中的规范场, 亦具有在该内禀空间的规范变换不变性, 用SU （ 3） 群表示[参阅“美哉物理（ 四 ）”]。此群有八个参量、八个生成元, 相应的有八个守恒量以及八种“ 色荷” , 即八种规范粒子—— 胶子[或可称作（强） 中间玻争子], 藉以传递“ 色作用” 乃至强作用。要将强作用与弱-电作用统一起来, 可采用以直积群SU （ 3）x SU （ 2 ） 又U （ 1 ） 为子群的更大的群, 诸如SU （ 5） 群等。当然, 这样的群的对称性又提高许多, 把强、弱、电磁相互作用均统一, 还能把每一代夸克一轻子（费米子）归入其“ 表示” 中； 共有二十四种规范粒子, 其中除了十二种是传递三种作用场的中间玻色子外, 还有十二种乃传递未知规范作用的未知规范粒子。至于把“ 大统一”理论进一步拓宽以囊括引力作用、以达成四种相互作用的“超统一” , 目前尚在探索之中。其试探途径之一, 依然是把对称群扩大。

对称群扩大、对称性提高, 由以构成的量子场理论体系的动力学涵义也就大为扩充, 实际上就可把越来越多的粒子及其相互作用的变化规律予以统一描述, 甚至可预言一些未知的粒子和未知的相互作用。看来, 量子物理与经典物理一样, 许多定律的确立都倚重于一些特定的对称性及其相关的数学形式, 而许多理论模型的构建亦都凭借于对对称性的探讨和对对称数学工具的运用。对称性研究确实在为理论物理的发展寻觅捷径、开辟通途。

对称性 并非凝固不化

对称性并非凝固不化、一成不变。“ 美哉物理（一）” 提及, 正、反粒子的电荷共扼对称性并不是绝对的。在宇宙极早期, 粒子过量是因粒子与反粒子的性质略有差异所致。这里且以C 变换、P变换、T变换为例, 说明物质系统的对称性必常常伴随以对称性的破缺, 二者亦是相反相成的。

C变换即为电荷共扼变换, 乃指将系统的所有粒子都变成其反粒子的变换, P变换和T变换就是空间反射变换（亦即镜面反射变换） 和时间反演变换。这三种变换往往是对于粒子系统之运动状态时而起到举足轻重作用的对称变换。图10-7 便是镜面反射: 两套衰变实验设施互为“镜像”。时间反演也不难想象。譬如说, 将录像磁带从正向放像到反向放像, 就是T变换。图10-8 甚为美观, 其中黑人黑马和白人白马的外形丝毫不爽,但二者既有左右方向的差别、颜色又相反； 杨振宁把此图喻作CP变换, 当然是比较适宜的。把黑白两色互换比作正反粒子的电荷共扼变换； 如果再想象驮人的马在奔驰,则可喻作CPT变换。由此图的对称完好显示了CP变换或C即变换的不变性。P变换、C变换、T变换的不变性对应于P宇称、C宇称等量子数的守恒。

众所周知, 李政道和杨振宁因图10-8 黑人黑马和白人白马提出弱作用过程中P宇称不守恒的假设而获得诺贝尔奖, 吴健雄用实验证实了他俩的假设。图10-7 表示吴氏所做的两套互为“镜像” 的衰变实验, 其中选定极化的钻60 核作为试样。⁶⁰C₀因弱作用而发生β衰变。这两桩互为“镜像”的β衰变所放出的电子的角分布并不相同（见该图下方的两个计数器的读数有别）, 表现出殊为可观的左右不对称, 这自然是由弱作用引起的。

李、杨、吴的工作披露了相互作用过程中的对称性破缺,P宇称守恒定律原来并不普遍成立。可是, 在P宇称不守恒的某些场合,更广义的对称性还是存在的。例如中微子和反中微子都只有一个相对的自旋指向: 中微子的自旋指向始终与其运动方向相反, 反中微子的自旋指向始终与其运动方向相同。这样, 中微子本身和反中微子本身都不左右对称, 而是中微子的“镜像”成了反中微子, 反中微子的“镜像”成了中微子, 即在镜面的反射下对称性破缺； 然而, 要是把中微子在镜中的“ 像”再变换成它的反粒子, 则又回到了原来的中微子。这表明在空间反射变换（P ） 和正反粒子互换（C ）的联合变换（CP ）下, 对称性依然保持。关于这一点, 李、杨已经注意到。后来在考查K 介子的衰变时, 又发现对称性在CP 变换下有新的破缺, 而必须再顾及时间反演（T ）, 即在CPT联合变换下对称性还能满足。在宇宙极早期, 正因为K 介子等粒子在CP变换下出现对称性破缺, 才使粒子数略微高于反粒子数。从P→CP→CPT,这个转化过程来看,粒子体系的对称与对称破缺确是相伴相随、潜在互动、有机地结合在一起的； 这是一个动态过程, 静中有动, 从而导致微观层面的美学趣味丰饶、盎然、非凝固化。

再看宇观层面, 其统一场的逐步分解更是一个生物演变的过程。现代宇宙学有如下设想: 在宇宙极早期, 能量极高, 所有相互作用完全统一（“超统一”）, 即只有一种统一的作用场； 以对称性而论,这时的对称程度最高。能量降低,对称性开始破缺, 引力场从统一场中分离出来, 强-弱-电依然“大统一” , 其对称性可用SU （ 5） 群表示。能量再降低, 对称性继续破缺, 强作用场与弱一电作用场分离, 二者各自的对称性可分别用SU （ 3 ） 群和SU （2 ） x U （ 1 ） 群表示。能量进一步降低, 弱作用场与电磁场分离, 这两个场各自的对称性自然都低于弱-电场。就这样, 随着对称性的不断破缺, 统一场最终分解成四种不同的作用场。这个过程若倒逆而观, 那便是上一节讲述过的: 由于能量渐次上升, 四种作用场一步步地统一, 对称程度也逐级升高, 最后成为一个统一场。由此得知, 各种对称形式都有其呈现范围, 倘若使其呈现的条件不具备,就会发生破缺。对称程度越高, 呈现的范围越广。所有的作用场达成“超统一” , 乃是对称程度趋于极致时量子场的极限状态。而通常,不同的物质系统虽都具有一定的对称性, 但同时潜在地伴有对称性的破缺趋势； 换言之, 不同系统在彼此不同的条件下, 因其对称性与对称性破缺以各自特定的方式相互制约、并达到辩证统一, 以致处于各各相异的状态。正因为对称形式不是单调划一、凝固不化, 物质世界才会多姿多彩、千变万化, 整个宇宙亦会不断地演化。

对称与对称破缺 物理美之无尽的源泉

对称-和谐-统一是物理之美蕴崇的三部曲, 对称是首部、是源头。人们往往认为, 大自然本来是对称与和谐的, 于是, 探索大自然的对称与和谐便成为大部分理论物理学家的共同目标。对物质世界的物理学描述及其理论构建, 常常都以是否具有显著的对称特征与和谐色彩为评判其优美与否的标准。例如, 麦克斯韦方程、爱因斯坦引力场方程、狄拉克相对论性电子波动方程, 都可算得是物理学中极为优美的方程, 它们的对称性都表现得淋漓尽致。麦氏方程充分体现了电与磁的对称性状, 是电场与磁场相统一的标志。爱氏方程使时空对称性提到至高水准, 以至于揭示了时空的动力学机制, 把时空几何与引力场统一起来。狄氏方程将电子波运动规律置于时空对称以及能量-动量守恒的基础上, 从而揭示了电子-正电子乃至正反物质这一深层次的对称性, 并使狭义相对论与量子力学在形式上结合起来。而各种量子场理论均同样地满足规范对称原理, 凭藉于规范变换不变性这个迄今物理学中最高级的对称形态, 可望使统一场研究登峰造极。“ 美哉物理（九）” 论述的“ 第一性原理” 和“第一性方程” 赋予物理学各分支体系以同一模式； 鉴于此, 物理学的和谐与美妙, 可谓无可比拟, 其各领域如果没有丰富实在的对称性和同一性, 彼此统一于同一模式当然是不可能的。

描绘物质世界之对称与和谐的物理理论, 其结构上的对称、简练、完整, 实际上就是所采用的数学表述形式的对称、简洁和完美。且看几例。经典力学的伟大成就和广泛应用乃凭借于微积分理论的精致以及变分原理的普适性。电磁场理论通过矢量分析工具, 把电磁场与电荷-电流的关联、变化的电场与变化的磁场相互影响的对等地位, 清晰地表达出来。复变函数论被认为是“ 最和谐的数学理论之一” , 而这正是使量子力学成为完备理论的主要缘由之一； 凭籍抽象的希耳伯特函数空间框架, 得以简明地描述微观系统之量子态的变化规律及其统计特色。量子场理论以及统一场论研究的逐步成功, 则如上文所述, 很大程度上得力于对对称群理论的适当应用。至于作为现代时空理论的相对论, 乃是利用阂可夫斯基空间的对称形式以及可容纳广义时空变换不变性的黎曼空间。如此等等, 不一而足。特别要指出一点, 物理理论的简洁亦是其主要的美学特征之一, 它亦起源于对称美。具有对称美的理论从结构到表述, 势必洗练、单纯、简捷。再者, 简单性原理正是理论物理的一个重要方法论原则, 循此原则,也就必然追求理论的对称和统一。

上文已述, 就物质世界本身而言, 其对称必导致统一性, 而对称之破缺则导致多样化。唯有对称、没有对称之破缺, 唯有统一性、没有多样化, 就谈不上美妙, 甚至也谈不上多姿多彩之间的协调和谐。相反, 对称与对称破缺的辩证统一, 才是物理美之无尽的源泉。在不同的场合, 破缺的方式不一。有的是外界干扰引起破缺, 有的是自发破缺（而且是一种更重要的破缺方式）。例如超导电性和反常真空, 涉及到的正是对称性的自发破缺。所以说, 物质系统纵然趋向于对称与平衡, 同时又有改变原有状态的自发趋势。李政道先生提出疑问: 很多物理理论都是根据对称产生的, 但为什么我们的世界又是不对称的？ 他并认为要从真空探索中寻找答案。一旦能解开这对称与对称破缺之关系的全部具体涵义, 物理学的理论结构和表述形式也就会随之更改。待到那时, 定会有更丰厚的物理之美被披露, 物理学内蕴的美学意义并会被揭示得更加透彻亮堂； 因为, 对称性毕竟是物理学、科学、科学美学中的一个至为关键的深刻概念。