美哉物理(九)

经典力学的后牛顿发展

继牛顿力学体系之后，拉格朗日-哈密顿的分析力学体系是经典力学发展史上的又一成功建树。众所周知，牛顿力学离不开牛顿本人所创建的微积分(流数术)，但他的《自然哲学之数学原理》一书阐述其力学体系还主要利用几何的直观形式，推理时必须用到的微积分乃采取其特殊表述的流数术。大数学家欧拉，将微积分表述成清晰简洁的形式，并由以重新阐解了牛顿的质点力学，进而还探讨、发展了刚体力学和流体力学。数学分析进一步完善，则促使力学体系得以拓宽。在牛顿和欧拉之成就基础上形成的拉格朗日-哈密顿力学体系，也明确地采用纯数学分析的完善表述形式，其理论框架并有所变更；此力学体系就称作分析力学。

《自然哲学之数学原理》于1687年问世；一百年以后，拉格朗日出版了《分析力学》(1788年)。成书之前二十年，拉氏依据」伯努利、达朗伯的工作成果，便已从两条重要的力学原理——虚位移原理和达朗伯原理出发，得出了动力学普遍方程。拉氏等人选取广义坐标作为独立变量，引人所谓的拉格朗日函数(拉氏量)，而由动力学普遍方程导出二阶微分形式的拉格朗日方程。

又过了将近五十年，哈密顿进一步扩展了拉格朗日分析力学。他添入相应于广义坐标的广义动量，将其也作为独立变量；由拉氏量转变成哈氏量——哈密顿函数。于是，他就将二阶微分形式的拉格朗日方程(组)转化成个数增加一倍的一阶微分方程(组)；此方程形式更为简洁、对称，被称作哈密顿正则方程。而后，又有所谓的哈密顿主函数的哈密顿-约可比方程建立，该方程对于求解能量守恒问题尤显简易。分析力学有微分、积分两种形式。拉氏方程和哈氏正则方程等属微分形式。至于积分形式，乃从对最小作用量原理的探讨起始。一般认为，该原理由莫佩蒂提出，其实对此最早作出确切表述的是欧拉，比他更早提及的可能还有菜布尼兹。各人对该原理的陈述方式不尽相同。粗略地可陈述为：凡物质系统运动变化，总是使其作用量为最小(或极小)，但也可以为极大，即只要稳定一取为极值便可，亦即实际发生的运动变化对应于作用量为稳定的过程。

变分法的发明使分析力学的建立和扩展有了简便的数学工具。变分法发端于雅各布 · 伯努利和约翰 · 伯努利兄弟俩以及约翰的学生欧拉的卓越工作，并由拉格朗日用于构建其分析力学。变分原理使分析力学的微分形式和积分形式相互等价、易于转换。作用量之变分为零(意指作用量取极值)，即可由以简捷地导出拉格朗日方程和哈密顿正则方程等。所谓哈密顿作用量，就是拉氏量对时间的积分；对应于实际发生的运动，其变分为零，即作用量取作极值。这就是哈密顿原理。

因此，该原理实际是作用量的变分原理，这作用量由拉氏量确定。变分法是普通适用的数学原理；在物理学各领域，拉氏量和哈氏量又是涵盖面极广的物理量。故而，哈密顿原理是物理学中最基本的原理，或可称作第一性原理。这是经典力学后牛顿发展的主要标志，也是物理学近、现代发展的一块重要里程碑。当然，此原理还是以牛顿力学为其理论基础的。

最小作用量原理的臻美旨意

物理学家考察具体的物理问题，常常以最小作用量原理为出发点，通过变分运算而导出物质系统的运动方程以表示其运动规律。所以，数学上的变分原理亦可谓物理学中一项可起颇大效用的方法论准则。牛顿质点运动方程可通过这样的推导过程得出；甚至如广义相对论里的爱因斯坦场方程也可如此导出，尽管它是一个相当复杂的非线性方程。其实，所有运动方程就是拉格朗日方程或哈密顿正则方程在其拉氏量或哈氏量对于不同物质系统取不同形式时的具体体现。

哈氏量H乃物质系统的动能T与势能U之和，即H=T+U；拉氏量L乃其动能T与势能U之差，即L=T-∪(一般就保守系统且受完整约束条件限制的场合而言)。所以说，H和L都反映了物质系统的能量状况。而上文已述，作用量S是系统在一段时间间隔(t₁→t₂)里L的累积数量，即：

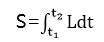
S取极值，其变分δS=0(S往往取极小值)。实际上，最小作用量原理意味着，一切物质系统的运动变化都遵循最大可能的经济原则；即上文所说的往往使作用量降到最小(或不很严格地说，乃能耗最小)。这符合一般的变分原理，而变分法便是自然界里普遍成立的一条经济原则。

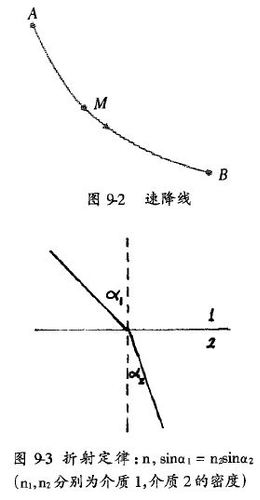
数学家曾详细讨论过两点之间的最短连线和最速降线；变分法正起源于这些数学课题。在地面上的直立平面内，一质点在自身重量作用下，沿某一条曲线从一点最快地降到另一点；这条曲线称为速降线。伯努利兄弟等人通过变分运算，确定速降线呈摆线(旋轮线)形状(见图9-2)。与此相仿佛，费马断定：光线在两种介质的交界面上折射，之所以满足折射定律(如图9-3所示)，也是因为循着一条最速路径(光程最短)。再者，自由粒子在平坦空间里沿(最短的)直线行进，在弯曲空间里沿弯曲的(最)短程线行进。这短程线满足的方程也由变分原理导出，其方法与推导速降线的相同。该方程与爱因斯坦引力场方程相洽，它亦是广义相对论的一个重大结论；而如前文已提及的，引力场方程的导出可采用引力场之作用量的变分运算。从光线路径和质点运动到四维弯曲时空中的短程线方程乃至引力场运动方式等等实例可见，无论是几何问题，还是物理问题，都可凭籍变分法去圆满地解决；特别是最小作用量原理及其在物理学各领域的成功应用，正就是利用变分法这一几何方法、亦乃经济原则去解析各物质系统之运动规律的丰盈成果。

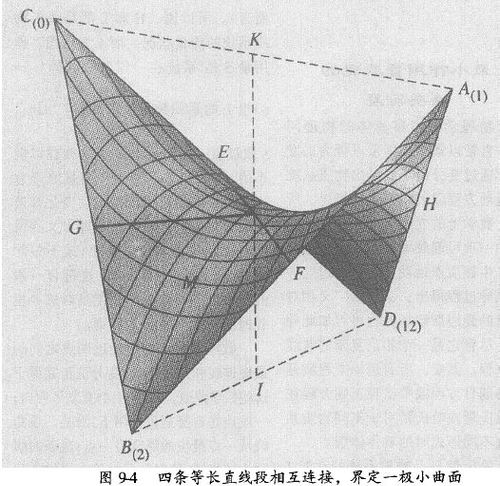
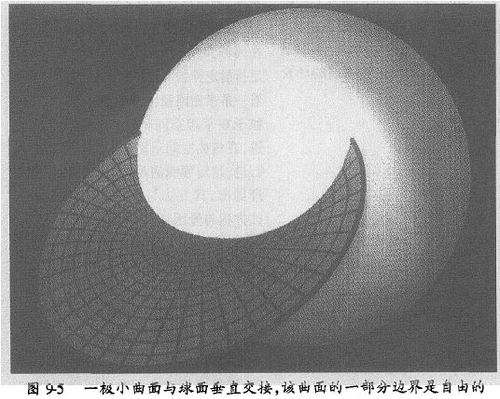
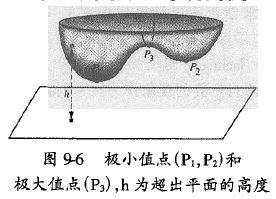
变分法作为一个简单、有效的几何方法，具有明显的赋美价值。作用量等取极值，则导致静止物体呈现平衡形态、运动物体呈现优越的变化方式；那么，最小作用量原理，或日哈密顿原理，也就显露出生动、丰富、瑰琦的臻美旨意。诚然，该原理是动力学原理；而静止1物体取特定的形态，亦有与其相似的缘由。例如，小液滴总是呈圆球形；张在闭合金属丝架上的肥皂膜？均为极小曲面(其面积极小)形态。此乃因为液面的表面能与其表面积成正比，曲面不论封闭与否，凡表面能极小以至表面积极小者才是其稳定平衡形态。相同体积的所有立体中球面的表面积最小，当然，球形的对称性最高；而张成不同形状的闭合围线的极小曲面可谓千姿百态，亦都富有一定的对称性，观之颇为赏心悦目。这里选载两幅极小曲面图*(图9-4、图9-5)，由其可见一斑。静止物体的平衡态有稳定和非平稳之别；比如对于处在引力场里的物体而言，稳定平衡态对应于(引力)势能极小，非稳平衡态对应于势能极大。如图9-6所示，小球在P，P2点时很稳；P3点虽也是平衡点，但小球在此并不那么稳定。

开普勒定律表明：行星沿着椭圆轨道绕恒星运行；牛顿用他的动力学理论对此作了严密的论证。而从哈密顿-约可比方程出发，同样可得出行星运行轨道一般为椭圆的结论，并且还可导出行星运行速度增大时，其轨道会演变成抛物线、甚或双曲线形状，至于圆形乃椭圆形的特例。图9-7所示的从圆→椭圆→抛物线→双曲线这一些圆锥曲线，正是天体运动的优美写照。牛顿力学描绘了天体运动的出色图景，拉格朗日-哈密顿理论描绘此图景也毫不逊色。当然，在经典力学范畴里，这两个理论体系本来是等价的，二者的臻美旨意也相仿佛。只是着眼点有所不同：对于行星运动，牛顿着眼于行星与恒星之间的万有引力；哈密顿等人着眼于行星运行时的能量守恒。正因为后者着眼于能量状况，遂使哈密顿原理的适用性得以超出经典力学范畴。

就是说，在力学以外的经典物理领域，哈密顿的作用量原理同样有效。例如电磁场，也可对其设定作用量，令其变分为零，便可导出著名的麦克斯韦方程。与离散质点系不同，物质场是连续性系统；亦有相应的连续性系统的拉格朗日方程，对于电磁场、引力场、流体等均适用。再者，哈密顿原理的应用还可越出经典物理。量子力学的核心薛定谔方程正可从哈密顿-约可比方程过渡得出。量子力学的三种表述形式与拉格朗日-哈密顿理论比较，都有其直接的对应物；当然，这里除了考虑到从经典力学过渡到量子力学的对应原理外，还须引入量子概念。其实，作用量原理在量子场论研究中发挥的效用最大；经典物理各动力学方程的导出，起先倒不必利用该原理，而建立种种量子场论，往往就是考查所研究之量子场的作用量，用变分法探索其变化规律量子物理学家乐于采用此法去展示微观物质层次的面貌。狄拉克认为：“哈密顿量对于量子理论是真正重要的；只有通过将哈密顿量或哈密顿概念的推广，才能获得成功。“因为”……从哈密顿量出发工作，确实是极为本质的”；而且由此出发的方法“有一个最大的优点，便是可以很容易使得理论满足相对性原理。”

看来，哈密顿作用量原理以及拉格朗日、哈密顿等人创造的凭借变分法的研究方式，的确能揭示许多物质系统的运动状况。物理世界的外观美(行星运行轨道、短程线等)和内在美(各种不同的运动规律)，全都聚焦于这同一条最基本的原理；这真乃大自然的造化神功。

“第一性方程”的最优性

如果把哈密顿原理称作“第一性原理”，那么也许可把由该原理简捷地导出的拉格朗日方程(或哈密顿正则方程)称作“第一性方程”。且把拉氏方程列出如下：(d/dt)(∂L/∂q_i)-(∂L/∂q_i)=0其中，q_i是第i个广义坐标。倘若系统内有n个三维质点，同时受s个约束条件限制，则系统的自由度为3n-s，相应地就有3n-s个独立的广义坐标。倘若是连续性物质系统，即某一物质场，虽有无限多自由度，但q_i代表场量，场量的个数当然不多。拉氏量L是系统的状态函数。前文已述，常有L=T-U。但L也可不取T-U的形式，它由所着眼于系统的某一特征而定。它可以反映系统是质点系还是物质场；也可以反映是经典物理系统还是量子物理系统。它可以反映系统之动能及其相互作用势的性质，也可以反映其他方面的主要特征，比如在广义相对论里，则反映引力场之四维时空的弯曲征状，如此等等。自然界中物质系统的多样性，就由这拉氏量的不同形式表达得淋漓尽致。

拉氏方程本身是关于L的线性微分形式，但因对于不同物质系统，L的形式相差甚多，故当它转化成具体的质点(系)运动方程或场方程后，有时会是非线性的。比如爱因斯坦场方程——关于时空度规的微分方程，因L及其作用量体现了引力场的自作用而包含非线性项。由此可见，物质运动的一些线性规律和非线性规律，竟然都可溯源于相同的数学方程。既然拉氏方程是各种物质运动规律的统一表示形式，那么不妨说它是物理世界的一个最优化的理性描述方式。对于一定条件下的保守系统，L可等同于T-U，直截了当地反映系统的能量性质。而在别的某些场合，即使L代表系统其他方面的特征，这特征还是与其能量有关；仍说广义相对论的例子，时空的弯曲本由引力场的能量-动量所引起。因此，拉氏方程揭示的是物质系统能量性质趋于极致状态这样一条基本的经济原则，表明系统真实的运动过程比其他一切可能的变化方式都优越、都经济；系统总是通过最简捷的途径达到最佳状态。姑妄言之，第一性原理和第一性方程的全部美学蕴含就在于其统一性乃至最优性，它披露了一个使人惬意的真理：宇宙万物的运动变化服从于一个统一的经济模式。

既然不同物质系统的运动变化同出一辙、服从于同一的模式，那么物理世界必然呈现和谐统一的美妙图像。拉氏量可以千变万化，从而把这幅图像渲染得斑斓多彩；不同的拉氏量满足同一方程，又使图像的各个片段彼此协调和顺。故而这第一性原理和第一性方程把物理世界的多样性和同一性融于一体。此物理世界包含种种物质系统的不同运动形式，包含宇宙物质构成从宇观到微观的所有层次。各层次、各系统的运动规律尽管有形形色色的特殊性，但都以同一的模式结合成为一个整体。这同一模式就把内涵宏富的整个物理学贯穿起来。

并且，任何物理理论都是物质系统运动的近似描述，各层次各系统的具体理论都有一定的适用条件；而它们的同一模式、即第一性原理和第一性方程的适用范围也还是有限的。笔者以为，若作如下广义定义：凡遵循这第一性原理和第一性方程的物质系统，就称为哈密顿系统；那么，迄今为止物理学主要研究的就是这样的系统。也就是说，凡满足此原理和此方程的物理理论，组成物理学迄今为止的全部理论结构的主体。至于上世纪中期开始红火起来的混沌物理、分形物理、孤立子理论、耗散结构理论等，则超越了这个主体规范；它们有另一番景象、另一派风光，它们会为当今物理学增添别的美学旨意，而且可能更为诱人、瑰琦、朦胧。

_____________________

* 引自《悭悭宇宙一自然界里的形态和造型》一书，该书的中译本于近期由上海教育出版社出版。