对概率的更深入了解,将使生活更安逸、更安全,甚至更有趣。
清晨6点45分,时控无线电的天气预报声把琼斯 · 坎迪达闹醒了。“气温,63°F:有雨,可能性30%。”据此,坎迪达穿了一件薄羊毛开衫去上学,而把雨衣留在衣柜里。
坎迪达(Candida)在8点15分登上了校车。她冒着突如其来的大暴雨,刚刚跑完那最后四条街,她的绒衣散发着湿羊毛的气味,她的头发浸湿得一缕缕柔曲地垂着。“今天本该只有30%的下雨机会,”坎迪达一边坐下、一边暗自思量:“眼下一想,我甚至还不理解那是什么意思呢。要下雨,是说本市30%的地区?或是说今天30%的时间?不管究竟是什么吧,我觉着就好像刚试了下运气,却输了。”
虽说坎迪达的理解有她的道理,但那两种解释都不对。天气预报说的是,在以往相同气候条件下,每100天普遍有30天下雨。而这一天也许会是70个晴天中的一天,但结果却是30个雨天中的一天。
和生活之中许多其他事情一样,天气预报有赖于概率——某事发生的可能性。保险统计员计算人均事故发生的概率,以确定汽车保险费。政府民意测验计算每一位候选人获选的概率。机场指挥人员计算两架飞机同时到达的概率,以制定降落方案。因此,决定是否要穿雨衣,在从民意测验中提名候选人,以及我们搭乘的下班飞机会不会降落前要盘旋几小时?所有这些,在很大的程度上都和人们对于概率的理解、分析和计算有关。
概率计算可以仅仅是简单的基础数学,也可以是涉及上千种因素的复杂过程。计算抛掷硬币时正面朝上的概率,就只需要最简单的公式——以成功的次数(正面的)除以两者似乎具有相同可能性的总合次数(正、反两面的)。结果,正面出现的概率是1/2,即两次里有一次。就像所有的分数,它还可用小数(0.5)或百分数(50%)来表示。
同样地,从一副52张的纸牌中抽出黑桃“A”的机会是1/52。在52次同等可能的抽出中,抽对的仅只能是其中的一次。当然,一副纸牌中有四个“A”,要抽任意一个“A”,就会有四次抽对的可能,因此,机遇也就更高些——4/52 。这个分数同样可约简为1/13。
我们不但可以利用数学来计算抛掷硬币或抽纸牌的概率,而且还可以依据实际地进行一系列实验来计算事件的概率。正如天气预报测定下雨的可能性一样,后一种方法是在经验的基础上确定概率。计算式也十分简单。假如在N次迹象或试验中有S次成功,那么,在以后的事件中,获得成功的概率就是S/N。例如,抛硬币100次,大约会有50次是正面朝上的。因此,出现正面的概率就是50/100,即1/2。抛掷的次数愈多,概率就愈接近1/2。
第一节课是英语,坎迪达将会碰上另一个随机现象。教师曾布置她回家阅读赖特 · 欧尼斯特 · 文森特(Ernest Vincent Wright)的一本小说。虽然标记符号注明这是一部值得注意的著作,但她读起来感到太枯燥而禁不住睡着了。今天,坎迪达侥幸地发现,摊在她面前的那一页上怎么会没有字母“E”呢。“E”在英语中要算是最常见的字母了,而实际上在这部5万字的小说里,字母“E”竟一次也没有出现过。
坎迪达认为这真是件了不起的事,她自己试着模仿作者的这一技巧,却甚至连一段也写不出来。Gadsby的无“E”文体绝非是偶然的。作者为避讳“E”显然是尽了很大的努力。因为单凭偶然性,即使是只写一页,而不用字母“E”,这个概率也几乎趋近于零。
怎么会知道它是如此之小呢?要计算这个随机现象的概率,我们首先必须知道任何一个字母可能是“E”的概率。如果我们数一下各种图书或报纸的用字频率,并制成图表,就会发现在每1000个字母中,各个字母是有一定的出现次数的。
用字频率告诉我们,假如随机地从任一作品中抽取一个字母,而它是“E”的概率就是132/1000,也就是0.132。换句话说,在每1000次抽取中,会抽到“E”132次。由于另外的868次将抽不到“E”,因此,抽不到的概率就是868/1000,即0.868。
两个单独事件共同发生的概率,是他们各自概率的乘积6假如任取两个字母,他们都不是“E”的概率就是0.868×0.868即0.753。刚才摊在坎迪达面前的那一页有780个字母,要算出那一页没有“E”的概率,就得用0.868乘方780次。这样计算太冗长而单调了,我们借用计算器算出的结果大约是:
1/1048即在1048次中仅有一次可能。
在碰到某一事件的概率非常小的情况下,我们可以认为,这一事件凭机遇几乎是不会发生的。但是我们怎样来表示“非常小的概率”呢?显然,像我们例子中所举的1/1048那么小的概率,我们可以断定Gadsby这部小说是没有可能的。
铃响了,英语课结束了。坎迪达到楼下教室去上她最喜欢的课程之一的生物学。这一学期,她们班正在学习研究遗传原理的遗传学。她喜欢这门课,因为它可以帮助她懂得色盲是怎样遗传的。像其他的遗传特性一样,色盲遗传是由概率的基本原理所控制的。
美国大约有12%的男性患色盲。坎迪达的父亲就是其中的一个。像许多色盲患者一样,琼斯(Ralph Jones)能看出红、绿色的深浅,但却不能敏锐而一致地区分两者。在一次学校舞会上,她父亲穿的蓝外套、绿衬衫和结的红领带,曾使坎迪达大为窘迫,现在由她帮她父亲选择衣服了。
早在1800年,英国化学家道尔顿(John Dalton)首次研究了色盲,他自己也是个色盲患者。因此色盲法语为Daltonism。然而,直到1960年,人们才知道色盲患者眼中的世界是个什么样子。那时,纽约市哥伦比亚大学的眼科学家格雷厄姆(Clarence Graham)研究了一名妇女,那位妇女一只眼睛患色盲,另一只眼睛视觉正常,她能正确地描绘色盲病人所没到的一切。
像所有从父母遗传来的特征一样,色盲是由基因脱氧核糖核酸片段传递的,这种基因决定了:我们人体像什么;人体又是如何活动的。在细胞核内、基因排列成线状样,称作染色体。因为红绿知觉基因在T染色体内,即女性染色体内,所以色盲是伴性遗传的。
男性从母亲那里得到一条x染色体,从父亲那里得到一条y染色体。女性从父母亲那里各得一个x染色体,共有2个x染色体。因为同正常视觉基因相比,色盲基因是显性遗传,所以女性色盲患者必须有二条带有色盲基因的x染色体。如果仅有一条x染色体带有色盲基因,她仅是一个携带者,就是说,她自己视觉正常,但将有可能把色盲基因传给她的孩子。男性视觉,不管是色盲还是正常,都由他的单条x染色体所决定,因为y染色体缺乏一种管理色素视觉的基因。
坎迪达和同学们正在尝试测定色盲遗传的概率,即在一个假设的家庭中,双亲视觉正常,而他们的孩子将是色盲患者的概率。学生们知道在美国12%的男性是色盲患者。既然每个男性仅有一条x染色体,可推测12%的x染色体带有色盲基因,而88%的x染色体有正常基因。在同学们的假设中,这个家庭的父亲视觉正常,所以他的x染色体也正常。
下一步测定视觉也正常的母亲是携带者的概率。这个概率就是她可能由遗传获得一条带有色盲基因的x染色体的概率。两个事件共同发生的概率是各个独立事件的概率之乘积,这是显而易见的。所以,一位母亲认她的母亲那里遗传来一个色盲基因和从她的父亲那里遗传来一个正常基因的概率是0.12×0.88,等于0.1056。她从她的母亲那里遗传来一个正常基因和从她的父亲那里遗传来一个色盲基因的概率也是0.88×0.12,等于0.1056。因为有两条途径获得色盲基因,所以色盲发生的概率是二个的总和——0.1056+0.1056,即0.2112——大约为21%。
现在来分析一下下一代人的情况。他们知道女儿认父亲那里得到一条x染色体,从母亲那里得到另一条x染色体。因为她必须要有二个色盲基因才会色盲,又因为她父亲的x染色体带有正常基因,所以她仅能从母亲那里得到一个色盲基因。女儿是色盲患者的概率为零。
儿子将从他母亲那里得到一个唯一的x染色体,而他的母亲有21%的机会是个携带者。如果母亲是携带者,她的儿子就有50%的机会得到一个色盲基因。所以,双亲视觉正常,而儿子患色盲的概率是0.21×0.50,即0.105。
坎迪达的祖父母视觉都正常,所以坎迪达认为她父亲患色盲的机会仅是10.5兔、她也推断自己是一个色盲基因携带者,因为她肯定从她父亲那里得到一条x染色体。幸运的是,色盲不是一个严重的医学问题。但是,这种病说明了在患有严重遗传病病人的遗传咨询方面,如何使用概率分析的成果。
离开生物班以后,坎迪达认为她已放弃了概率分析,她不知道回到家后,还会遇到概率问题。那天晚上,咮饭前,她哥哥西蒙尔(Seymour),一个社会大学的经营系学生,请她一起做一个游戏。
西蒙尔请她选择一个三联组。通过连续抛三次硬币,根据所获得的正反面,这种三联组有八种可能的结果:HHH,I1 TH,THH,TTH,HHT,HTT,THT和TTT(H代表正面,T指反面)。坎迪达选择了HTH,西蒙尔选择了HHT。目的是通过往上抛硬币,直到某个序列三联组出现。谁选的一组先出现,谁就赢。
开始几次,出现的顺序是HTTTTHTH,坎迪达赢了,因为最后三个硬币正好是HTH。后来的每次比赛,坎迪达和西蒙尔各选择不同的三联组,不久坎辿达的运气就不佳,在下十次比赛中,西蒙尔赢了七次。她不知道西蒙尔运用了概率分析的战略,这种战略使西蒙尔总是起码以二比一的可能性获胜。
如果坎迪达选择的一组以TT开头,或以HH开头,西蒙尔就挑选HTT或THH。他的一组的最后二个选择与她的开头二个相同,但是第一个是不同的。如果坎迪达选择,以TH或HT开头的一组,他就分别选择TTH或HHT。也就是说,他以坎迪达的第一选择作为他的第一、第二选择,而把坎迪达的第二选择作为其第三选择。西蒙尔让坎迪达先选,这不是出于兄妹般的宽厚,而是因为他策略上的需要。
西蒙尔的成功取决于让坎迪达先选。那么,如果坎迪达选的一组前二次抛掷是一样的(正面或反面),西蒙尔就选一组最后的两次抛掷与坎迪达的前二个相同,但是他的第一个与她的不同。
为了找出他要这样做的原因,让我们用标记XXX和XXY来表示坎迪达的选择,XXX可代表HHH和TTT,XXY可代表HHT或TTH。西蒙尔的相关选择,不管是THH还是HTT,都用YXX来代表。
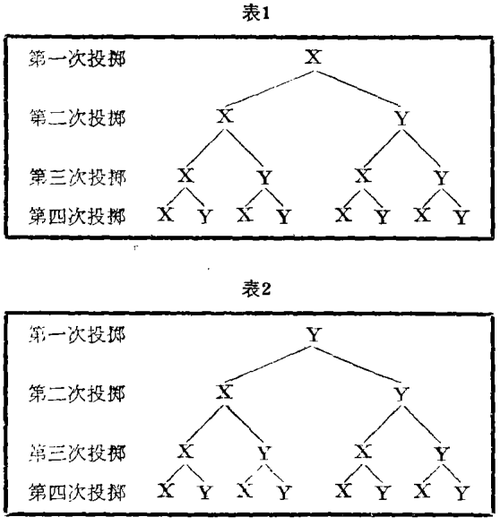
下面我们作两幅枝状表。第一个表表示当第一次投掷是x时的各种可能结果。
这里第一次投掷好像对坎迪达有利。然而只有第二次投掷也是x的话,才真对她有利。如果确是x,她就有了取胜的基础。因为假如她选择的是XXY,而最后投掷产生的是Y,她就赢了。
假如她选择XXX,最后投掷产生X,她就取胜,然而如果第三次投掷产生Y,她就丧失了对比赛的控制,因Y是西蒙尔选的三联组中的第一个符号。
如果第二次投掷产生Y,比赛实际上是西蒙尔的了,因为在他选择的三联组中,第一个符号是Y。如果接下去的一次投掷还是Y,西蒙尔不管是获得还是丧失取胜的基础,都能控制比赛。如果下次投掷产生X,他就差不多完成了他的三联组而取胜。这时,坎迪达没有取胜机会,因为在她的一组中,必须有2个连续的X,而即使有两个连续的X,前面有个Y,都仍然是西蒙尔获胜。
这样,如果第一次投掷产生X,西蒙尔赢得比赛的机会是一比二,因为第二次投掷产生Y的机会是一比二。
在第二个分表中,第一次投掷产生Y,很明显,西蒙尔将肯定获胜。
只要出现西蒙尔就控制了比赛。只要两个x连续出现,他就取胜。既然任何两个x连续出现,前面必是Y,那么坎迪达必败。
研究了这二张图表后,你能看到二次投掷以后,有四种可能性相同的结果——XX,XY,YX,YY——在其中的三种情况下,西蒙尔一定能取胜。他赢得比赛的可能性是三比一。
如果坎迪达选择XY(HT或TH)作为三联组中的前二个数码,西蒙尔能选择XXY反击,虽说这时他取胜的可能性比第一个例子稍少一点,但仍然对他明显有利,这点可以通过制作一个更为详尽的枝状表来证明。不过,只要让坎迪达先选,西蒙尔总是回报一个可能性对他有利的选择。
西蒙尔用二个完全相同的棕色购物袋和许多扑克牌筹码,尝试与全家人做另一个游戏。他把14个白筹码和6个蓝筹码放进一个袋里、把14个蓝筹码和6个白筹码放进另一个袋里9因为第一个袋里放的白筹码多,他称它为白袋,则第二个称作蓝袋。然后他告诉坎迪达把二个袋拿到另一个房间去,再带回一个。西蒙尔不知道她带回的是那一个袋,也不能看袋里的东西。他从袋里抽出一个筹码,是蓝的。他把这筹码放回去,摇摇袋子,另取一个。这样重复10次以后,他抽了7个蓝筹码和3个白筹码。
西蒙尔请家里人猜一猜他刚才所抽的口袋是蓝袋的概率——蓝袋就是内装14个蓝筹码和6个白筹码的口袋。坎迪达猜60%,西蒙尔微微一笑。然而,这天早上,在工业管理班上西蒙尔也是以50%回答他教授的这一问题的。其他学生回答的范围很大。
西蒙尔和个别几个学生坚持说这种概率是50%。他们认为以这种抽取是不能决定蓝白口袋的概率的,这种有色筹码的顺序能来自任一口袋。少数几个学生估计这种概率是60%,他们认为这种抽取对蓝袋的概率有利,但这种概率不会太大。大多数学生猜测这种概率是70%或80%。学过概率课的科学家们和学生猜测为80%0少数几个学生认为这种抽取非常有利于蓝袋的概率,他们猜测90%。
通过一系列有关的计算,正确的答案是一个令人吃惊的数字97%。确切地说,这十次试验足以说明坎迪达带回的口袋肯定是蓝袋。
西蒙尔的游戏告诉我们二个重要的经验,第一,极少几次的抽样足以用来精确地估计行为,这本来仅能由非常广泛准确的测定才能决定的;第二,即使在相当简单的概率问题中,人类的直观并非都很灵。
晚饭后,坎迪达去超级商场买一些巧克力。她的两个同学在同一天过生日,她的任务就是带些胡桃巧克力到家庭生日宴会上。坎迪达认为,在一个班级的25名学生中,有二人的生日在同一天,这是很不寻常的,然而机遇却创造了这种可能性。
为了测定这种可能性,我们以某个学生的生日为基准。至于到底是哪一天,这与计算毫无关系。第二个学生和前者生日不同的概率就是364/365(分子是生日不相同的次数,分母是可能的答案的总次数)。三个学生生日不同的概率是364/365×363/365,同样,四个学生生日不同的概率就是364/365×363/365×362/365。
当一间房子里的人数多于22个时,就可能至少有二人生日相同。在25名学生的班级里,所有生日不同的概率是0.43。因此,1-0.43,即0.57,是至少二人生日相同的概率。换句话说,生日相同的可能性是0.57比0.43,即4比3。
这似乎是预测二人生日在同一天的可能性的落后方法。然而,要计算所有的学生生日不同的可能性是一个简便得多的过程。随着学生人数的增加,其中可产生二人生日相同的能组合的数量也逐步上升。例如:两个学生(A和B)可能同享生日的途径只有一条。而对四个学生(A、B、C、D)来讲,其中任意两人同享生日的途径却有六条:A与B,A与C、A与D、B与C、B与D和C与D。因此,在计算所有生日不同的可能性时,每考虑一个学生,我们只要从分子不同生日的次数中减去一天就行了。
在超级商场,坎迪达选择了结账队伍最短的一队。然而队伍一点也不动,因为她前面的一位顾客正在和店员争论标在一罐橄榄上的已模糊的价钱。坎迪达又一次变成一个机遇游戏的无意的参与者——这次涉及到排队等候问题。
对付排队等候问题,分析家们要研究队伍的可能长度,和在各种情况下,排队的人们等待服务所需的时间。
坎迪达在结账柜台的耽搁只不过加重了负担,而载有贝尔法 · 约翰斯的大型喷气式飞机在拥挤的天空上停留是危及生命的。假如飞机是在有规则的飞行间隔到达——如相隔一分钟——假如每架飞机在跑道上都要54”——这类停留就很容易避免。从理论上讲,在4:04到达的一架飞机用第二个54”着陆,在第二架飞机到达前6”内跑道上没有飞机。跑道只用了54/60的时间,其他时间是空的,因此飞机永远不会排队。
但是,现实世界永远不会如此完美。实际上大多数飞机不是迟到就是较时刻表稍微早到一些。这样,在一个正常的星期五下午,就会出现临时性排队。飞机安排得愈紧,排队愈严重。例如,如果我们安排每54”到达一架飞机,我们可以预计有很长的排队:如果我们安排每二分钟到一架,排队就会大大减少。
星期五下午,每条航线都想安排尽可能多的飞机着陆,对此机场管理人员和联邦航天局必须决定下午4 ~ 7点钟可安排多少架飞机着陆,避免排队等候致使飞机不得不在空中盘旋直至耗尽汽油,或使担惊受怕的驾驶员转向另一个机场降落。
飞机是否会在空中排队等候,其后果如何,对此数学难题尚无简单解决办法,因为飞机是随机到达的,比如,机场管理者无数学公式来推算7架飞机在空中的排列情况。
要决定下午4 ~ 7时对安排多少次着陆,机场管理者必须使用一个表格来进行反复试验和误差计算。他也许只能略作猜测,说180次,然后在几个月里对此估计进行检验,以观效果。如果180次着陆无大问题,可以接着试200次,以此递增,直至出现问题。但做该试验时不能影响正常的飞行及航线上的乘客,因此机场管理者就得改用一种模拟办法,根据机场完全相等的条件作一个系统的数学分析。
首先要记录全部有关事项。如:每架飞机着陆时间为54秒,降落是随机的,降落率为1分钟。如果他以6秒钟作二次降落的间隔,一架飞机到达的概率便为6/60或1/10,间隔如此之短,几乎很难有任何机会两架飞机同时着陆,也可以试用5”、3”或1”的间隔。随着间隔缩短,模拟变得更为精确,但计算也相应变得更冗长了。到达间的平均时间以1/10为间隔是理想的。
现在机场管理者把下午4 ~ 7点这三小时分为1,800个6”间隔。因为这段时间共计10,800”,相应的间隔就有1,800个,然后用1到1,800的间隔次数来测算时间。
第二步,假设一个星期五下午的一次模拟航空,计算每架飞机的到达时间。由于每个间隔中到达的可能性为1/10,机场管理者也设了同样的情况。他在图书馆找了本有关随机数的书,书中的数码是由某个人或计算机任意选出的,诸如抽取帽子的号码等。因为书中只有双号,他要找的是单号,就要把双号拆开来看。他规定每个数字表示一个间隔,仅一个数-6表示到达。他翻到一页开头是:
29 14 16 35 67 22 08 19 40 65
因为机场管理者已经决定第6号代表一次到达,所以第一个号码2表示在第一个6”间隔中没有飞机到达。实际上在第六个间隔出现时才有飞机到达,而这时有一个6字出现。他注意到在间隔9和19时也有飞机到达。他不断试验,直至试完了第一个1,800号中全部的6,模拟了下午4 ~ 7点间到达的所有飞机。
现在他能画出一张图表。A机在间隔6到达,飞行54”,或9个间隔。B机在间隔9到达,等到间隔15才着陆,飞了15 ~ 24个间隔。在C机到达前B机一直在飞行。
在画完了全部1.800个间隔的图表后,他得到了一个图像,即3个小时内所有飞机到达次序的排列图。这样他就可以找出某几架飞机,如3架飞机可能在空中分层盘旋等待着陆的平均等待时间和全部时间,并设想该系统的工作程序。
经过这次模拟“飞行”,他只得到了假设条件下的情报信息。也许这个星期五十分走运,飞机几乎没存在空中排列,但也可能是罕见之拥挤。事实上他已建立了一个飞机到达的时刻表,并作了一次试验,但他还没有充分理由来决定是否采用这个程序系统。
所以他使用了另一组随机数字来重复进行该试验。经过十几次试验,他就能决定这个预定时刻系统是否可以应用。倘若不行,还可以试验另一个预定时刻计划——也许把到达时间改为57”。
由于是模拟,他可以对一个系统的各个性能进行试验。他可以轻而易举地让模拟来描述航空控制减速或需65”着陆和起飞的大型喷气式飞机。当他在模拟中作这些变化时,便能看到等待着陆的飞机行列的变化情况。
该可行性模拟可用于各种排列问题,诸如设计超级市场的结算柜台和高速公路的收税门等。寻找两个极端的最佳折中方法,即:没有排列次序和尽可能使顾客满意,或是在一个服务途径上削价与一长列不满意的消费者之间,这是一个单位的管理者要不断面临的难题。超级市场的管理者可以不断调整他商场内的这个系统,当排列似乎太长时就可以再开设辅助的结账柜台。
有许多项技术能减少顾客长期等候的烦恼。例如,在一些面包房和糖果店可要求顾客取一个号,然后根据先到先卖原则来处理。许多航线的票房柜台和银行已在若干办事员和出纳员的位置上建立了一个单位排列系统,如果Candida的超级市场使用了这个系统,它就不会为顾客的等候等问题发愁了。
1900年前,可能性分析仅为赌徒们原始地用来核算机遇比赛中的运气之类。此后,科学家、医学家和工程师们也开始研究这个差额(可能性),他们运用可行性分析来预测地震,估计心脏病人发作的时机及决定在一条收税路上的收费亭位置和号码。将来,我们可以寄希望于可行性分析在分配能源、选择人工心脏接受者和设计更复杂的计算机比赛中起作用。
我们无法控制随机事件——气候变幻、掷分币或人类和自然界的灾害。但可行性分析可以使我们的世界变得更安全、更可知和丰富多彩——甚至更奇妙有趣。
[Science year,1982年]