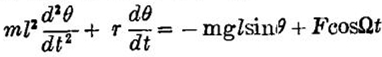物理学家们大部分只关心简单性,从复杂的世界中抽象出来的简单性。比如牛顿发现了能预测行星运动的简单规律。从原子物理学得出的结果表明,薛定谔方程是几乎所有能观察到的原子的行为的正确描述。事实上,氢原子结构理论,在物理学的各个领域,都作为一个有启发性的例证,说明我们如何寻找简单性。
从某种意义来说,这种对简单性的寻求,使我们对这个世界的描述,有点类似于一幅稍微歪曲的漫画,而不是一幅如实的肖像。大部分初等物理教科书所描述的世界,是一个充满了简单性、规则性和对称性的系统。这使得学生可能有这样的印象:原子物理就是氢原子,在日常生活中经常碰到的各式各样的电磁现象,就是平板电容器或偶极辐射。规则的结晶态固体就是材料的典型等等。在标准的物理学课程中,有流体力学这一门课,它十分充分地讨论了物理学定律可能演化出什么复杂的结果,但这门课现在已很少讲授。我们所谈到的这些学生,如果用无偏见的眼光看这个世界,他将会发现这个世界要丰富得多,没有一件像物理学教科书中所描述的那种样子。在真实世界中,简单性是极稀少的例外。海上的波浪搏击海滨,破碎后产生涡旋、泡沫和浪花。每一个行星都与另一行星不同,有些带有卫星,卫星之间又各各不同,有些带有漂亮的光环。原子及分子光谱表明:有许多特性不同的能级即频率差,以及十分丰富的不同的光谱线结构,它们是从未在氢原子的光谱中观察到的。甚至“基本粒子”物理也包含极大的复杂性,使其虚有“基本”之名。基本粒子世界在从毫电子伏到几百个千兆电子伏的能量范围内,几乎每一个能量级都有它自己特有的现象。我们周围的世界,复杂性虽然是最明显的特点,但是物理教科书的描述,总是忽略了世界的多样性,或者把它们当作一种迷乱来处理,然后选择一些简单的情况来绕过它们,并给我们自己'一个“有代表”性的例子。
上面我描述的图景是极端的情况,其实物理也注意理解复杂性,特别是其中应用性更多的那部分。这里所谓应用、不是指商业应用,而是指那些在真实世界中产生的、特定类型的系统。例如,天体物理学家必须了解的,物质在宇宙中的分布。生物物理学家所提出的,生命的起源。等离子体物理学家所必须处理的,电离气体的涡旋中的流线的互相缠绕的结构。至于固态物理化学家,则要注视 - 块钢铁的晶体结构。上述这些科学家们都以处理复杂性为其每日的课题。直到现在,很多物理学家都把上述例子看作是“不纯正”的物理学或“贫困”的物理学,而不予考虑_可能认为这些例子中所含的才智内容,不如一个,比如说,简单而容易解释的光谱多。在本文,我想提出一个相反的观点,并探讨其可能性,即:在我们周围世界中所观察到的复杂性,提出了一些问题,它们对理解物理定律的本质是最为基本的。其中三个问题是:
· 非常简单的物理定律是怎样给出错综复杂的结构的。
· 为什么这些错综复杂的结构,在我们观察到的世界中,如此处处存在,随时显现。
· 这些复杂结构常常是各该类简单物理定律的具体的显示者,为什么会这样。
在物理学内部及其周围,有一些学科确在研究这些复杂性,并认为不论就复杂性的普遍性或其特殊性来说,均存在某种值得感兴趣的东西。特别是上述那些较易研究的存在于流体力学、天体物理学、固态物理学、激光物理中的例子更是如此。这些研究题目现在已经有了各种名称,但最流行的名称是“花样形成”或“混沌”态。从这些研究中萌发出一些重要的概念,下面我要描述其中之一个。
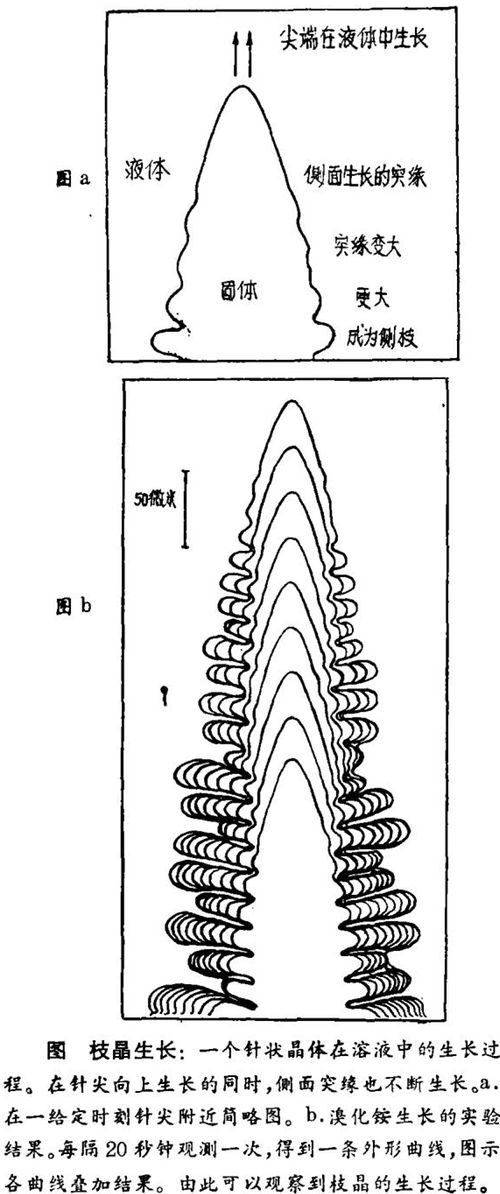
在一个已经确立的物理定律中,又产生出复杂性,其主要原因常常是:对初始条件有很灵敏的依赖性。这种灵敏性可在结晶固体冷却,枝晶生长这一过程中直接看到。在条件适当时,结晶固体会在液体中向上生长,成为针状物,并在外周有突缘,类似于葫芦环(图a、b)。每一突缘都是在固化过程中的不稳定性产生的。突缘开始时在靠近针的顶部形成,其时它们非常之小。随着时间推移,针尖向前移动,而不稳定性便使每个突缘长大。最后,这些突缘形成复杂的形状,具有许多旁枝,好像从侧面把针拉出来一块似的。这些旁枝的高度和位置都很不一样。因为每一个旁枝都是起源于最初在界面上的微观扰动,后来经逐渐放大而成。因此,所观察到的结构的种种变化,都是由于晶体生长时,对生长条件有十分灵敏的依赖性。这种敏感性多次重复,便是自然界复杂性的主要来源。
枝晶是一个例子,表明混沌的不可逆增长。雪花的生长也许是一个更熟悉的例子,并且是一个粗略的相似物。另外一个例子是在一个封闭的环境空间内发生的运动。此时,描述此系统的变量,永远不能越过一个有界区域。在某种意义上说,这个系统必须不断重复做同一件事情。如果这种系统呈现出对环境条件的灵敏性,并且此灵敏性不断重复,那么它也会变成混沌状态。它将在其有界区域内遍历可能的各个状态,每次往复运动都与以前任何一次不同。这个系统永不会精确地重踏同一路径。
这类混沌行为的典型例子,为一个阻尼摆(锤)受一个周期外力所推动。描述此运动的微分方程极简单。若摆的角位置变量为,质量为w,长度为I,则方程是:
若正确选择阻尼常数r,力强度为F,外加力的频率为Ω,那么这个运动永不会准确地重复自身。
此外,也有极好的理论及实验,描述当运动方程的参量变化时,这类系统如何从有序变到混沌。但我们现在仅限于理解这样的系统,即这种系统可以用几个变量或激发方式来描写其运动。流体力学系统能呈现出丰富得多的行为。在那里,旋涡套旋涡,并且对状态条件有灵敏的依赖性,这种依赖性在许多互不相同的尺度上同时、并发存在。要了解这一完全紊乱的行为,到现在仍未成功,尽管已有几个使人鼓舞的迹象。
因此,对学生提的问题:“为什么物理定律如此简单,而真实世界如此复杂。”正确的回答是:让我们进入物理学并找出答案吧。
[Physics Today,W87年3月号]
——————
* Leo Kadanoff系凝聚态理论物理学家,美国芝加哥大学物理学教授。