J. 斯威夫特(J. Swift)在1733年有诗曰:
科学观察惟仔细
蚤身复有小蚤栖
大蚤之血小蚤咬
循环往复无止息
这首诗反映了物理科学和生物科学中一个激动人心思想的基本特征,这个思想就是:我们在众多自然现象中观察到的动态活动,是许多不受注意层次的运动结果;这个难以察觉的运动,通过一个尺度因子,使运动从一个水平到另一个水平互相关联起来,斯威夫特看到了尺度间的自相似性:在最大尺度上观察到较小的运动图形,当观察的尺度越来越小时,运动图形的大小将以逐渐减小的方式不断重复。具有这种特性的过程,如今称之为分形。虽然不存在任何简单的分形的定义,但所有致力于简单定义的尝试,均包含“整体是由以某种方式与整体相似的部分组成的”这样的思想。
在描述动态过程时,对过程起作用的各种时间尺度(频率)形成一个特征谱。这个谱表明此过程的能量如何分配给不同种类的运动。该种过程的一个实例是简单谐振子,它具有单一频率组成的谱。相比之下,随机时间序列具有一个很宽的谱,因为许多频率影响内在的动态特性。但分形过程或分形时间序列却迴然不同。就分形过程而言,不存在任何特征尺度,其频率组成反幂律谱,即l/fα,其中f为频率,α为正数。
当然,人们既会谈到空间序列,也会论及时间序列,在空间序列中,频率对应于每米周数;在时间序列中则对应于每秒周数。无论哪种情况,反幂律谱都显示出内在过程的分形或尺度不变性质。许多蕴含分形或尺度不变特征的自然现象,都叫做1/f现象。
1738年,当D. 贝努利(D. Bernoulli)设想把某量叫做效用函数时,他实际上指出了1/f现象的重要性。贝努利对刻划个人行为的特征饶有兴趣,并用效用函数来描述个人的社会福利状况。他认为某种非特定的量f的变化量?f,对依赖于已拥有多少f的不同人来说,具有不同的含意。例如,若f表示一个人的收入水平,则收入水平越高,收入的任何异常改变?f越无关紧要。若两个成员的?f/f比值相同,贝努利便断定由收入不同的两个人所做的交易相等,也就是说,交易包含有各人收入的相同份额。
贝努利认为个人交易的效用函数由方程U(f)=log(f/f0)给出,这里f0是维持生命必需的某临界值。当U(f)具对数形式时,效用函数的变化正好是?f/f。此对数函数与f的单位无关,也不依赖于过程的尺度,效用函数的导数给出1/f性态,反之,?f/f的积分得刻对数效用函数。该对数及其相对变化的尺度不变性,将再三出现在我们对1/f现象的讨论中。
我们知道,个人的社会行为不能由这样简单的数学形式所表示,尽管有许多生物系统和大规模社会系统的性质能如此描述。我们所看到、嗅到、尝到以及所体验到的任何事物,都处于连续的变化过程之中。但世界的变化不是一成不变地体验得到的。G. 费克纳(G. Fechner)在上个世纪通过实验确定,人对刺激的反应不取决于刺激的绝对水平,而取决于刺激的变化率。假若频率为刺激作用,则我们对?f/f的反应较f本身更甚。这项早期工作证实了贝努利的直觉,即便其基础是生物学的而不是社会学的。我们目前已认识到,人类正是以这种不相称的方式对各种刺激作用(包括作用于皮肤的电击、灼热和压力,以及提起重物等)作出反应。由此看来,包含尺度不变性的对数函数logf比函数f,能以更自然的方式刻划生物和社会现象的特征。
有证据表明,一个现象的1/f特性与其复杂性有关。复杂系统由大量产生不确定性的相互作用组成。这种动态不确定性或无规行为被归入噪声时行列。按照确定性观点,我们只能预测过程可能的未来状态,而不能认识复杂过程的演化。可能的未来状态的谱由概率分布函数给出,它描述系统的复杂性,而与其机制的细节无关。就复杂系统而论,这种概率分布函数形式,的普适性,表明了无处不在的l/f现象的本质。
从正态到对数正态
每个一年级大学生都熟悉众所周知的正态分布,他们会得到一个基于钟形曲线的分数。19世纪英国古怪的S. F. 高尔顿(S. F. Galton)曾这样谈到正态分布:“我知道万物几乎无不如此易于铭刻为图形,成为‘误差频数定律’表示的井然有序的不可思议的形式。虽然古希腊人了解这个定律,但他们仍然把它人性化甚至奉若神明,这个定律以宁静和在最无序的混乱状态中完全隐蔽的方式支配—切、民众越多和明显的混乱状态越厉害,则其统治越完美。它是无理性的至高无上的自然法则,无论何时控制和以其量值的数量级安排大量样本的混沌元素,一种出乎意料、美丽无比的规则形式始终潜在。”高尔顿指出了这样的事实:在正态分布中(和在其它分布中一样),系统整体上看到的规律性和稳定性,与系统的个别元素的可变性截然不同。
高尔顿搜集了孪生子的特征、打呵欠的频率、个人的寿命、女继承人的不育、肉体和精神特征的遗传等的统计资料。他把正态分布引入社会科学以及人类计量和行为的统计学,尽管高尔顿赞美正态分布,但他还认为由几何方式较代数或调和平均方式,可较好地描述某类事件。换言之,此过程与其用正态分布,倒不如用对数正态分布会更好地得到描述。
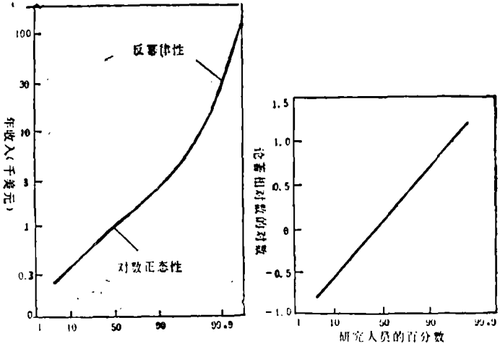
只是在给定变量的对数情况下,对数正态分布就是常见的正态分布;也就是说,若x是给定变量,则当已知X的对数时,分布看起来是正态分布。如logx,分布函数本身即为尺度变量。西方社会的个人收入,至少部分是具有对数正态分布的过程的例子。图1显示97%的收入水平为对数正态分布,其后的分布光滑地偏离对数正态分布。我们把收入分布与一具有正态分布的过程——人的高度——作个比较。从高度的分布,我们感到偶遇比你高50%的某人的概率是有限的,而遇到2倍于你身高的某人的概率非常接近于0,遇到10倍于你身高的某人的概率肯定为0。再考虑收入的分布。碰到某人10倍于你的收入的概率不为0,碰到某人100倍于你的收入的概率也不为0。处在收入的极端数值时,这些有限的概率水平就是收入分布中的长尾。
之所以出现对数正态分布的理由,是基于苏联数学家库尔莫果罗夫(A. N. Kolmogorov)提出的损耗理论(theory of breakage)。他在研究收入分布的问题时所采取的方法是:首先假设达到某一收入水平是一个复杂的任务,它由一系列子任务诸如社会背景、教育水准、个性类型、技能、交流能力、动机、天时地利,以及冒险等组成。然后对各成员规定分别实现8个因素的一系列概率。则个人的收入水平正比于8个概率的积P1P2…P8。按照库尔莫果罗夫变更的论点,若这个乘法的假设是正确的,则收入的分布是对数正态分布。对直至97%或98%的总体情形,图1显示了这一点,余下的2%到3%显著偏离对数正态形式:因为分布变为受反幂律支配。这将在后面讨论。
图1. 左边的双对数图中,可见美国1935—1936年的收入在主要区域遵循对数正态分布(近似为一条直线),在弯曲部位之上遵循反幂律分布。许多通常所说的1/f现象,在较高区域均呈现这种反幂律性态趋势。如同收入的情形一样、科学家发表的论著数目也是对数正态分布(右图)。图中的对数正态特性未表现出反幂律,因为此结果是根据不足100名科学家的研究人员得到的。数据是晶体管的发明者肖克莱(Shockley)收集的,他指出由于有大量因素影响出版发行,所以论著是对数正态分布。
显然,在上述例子列举的因素中,或许遗漏了某些重要因素,包含的要素也不一定十分恰当。但是,这些考虑都不改变观察到的分布,因为在给定收入水平实现之前,必须成功地完成大量的子任务。正态分布和对数正态分布间的区别,可由两句俗语的对比来形象说明:“足骨连踝骨,踝骨接胫骨”——表明组成人体身长的骨头的依附性;“掌钉在时掌不在,马掌在时马无影”——表明互相依存事件的乘法关系。在第一种情形中,若丧失一个要素,则后果较小,而在第2种情形中,个别要素的缺失,会导致整个过程失败。事实上,正是对数正态过程的乘法(而不是加法)基础的这种隐含的连通性,引起对数正态分布的长尾,这就与经济学家称谓的比例作用定律有关,此定律指在任何阶层的变量(个人收入水平)的变化,是其当前值的无规比例;即非尺度比?f/f是一个随机变量。
从对数正态到1/f
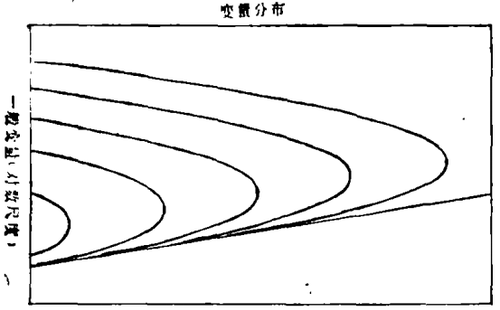
当对数正态系统变得越复杂时,其分布就越宽广,而且它们具有与1/f性态有关的量也越多,这种趋势示于图2,其中5个对数正态分布对应于复杂性和噪声的增加,呈现宽度递增。在图2的对数尺度中,1/f分布是斜率为负的一条直线。正如所见,当对数正态分布的宽度增加时,1/f分布和对数正态分布重合的区间大小也增加。实际上,对于欲完成的主要任务来说,必须实现的子任务越多,对数正态分布和1/f分布之间无法分辨的f的值域越大。
图2. 当对数正态分布变得较宽时,相当于系统的复杂性增加,它们与反幂律分布(显示在这里为一条直线)大部分重迭。这说明渐增的复杂对数正态现象,更多地表现出反幂律支配系统的分形或尺度不变性特征。
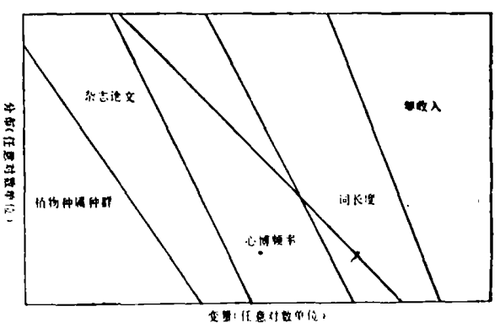
另一个遵循反幂律或1/f分布现象的例子是词使用的频率。长词较短词更少使用,从而一种语言的词汇按其使用的频率排列,产生一递减的对数正态图(图3)。词的长度正比于产生词(无论用写、说或其它方式)需要的时间,所以我们能使词长度与关联时间相关,若我们假定对于语言没有任何特征时间尺度,或相应地无任何典型词长度,则我们断定语言肯定是一种1/f现象。事实上这已由G. K. Zipf所测定。他发现就词使用的频率而论,许多语言具有反幂律,但不同语言间斜率略有变化。尺度不变性和实验语言学之间的关系,是一个充满活力的研究领域。
图3. 反幂律至少部分决定惊人数量的社会生物学现象。5个全异的现象以任意单位对数轴如上作图,使得反幂律为一条直线。左起是:植物种属内的种群对含此种群的种属数作图;杂志发表的论文数目对发表此数论文的科学家数作图;心脏搏动包含的频率对此频率的出现情况作图;英语的词长度对各句的使用情况作图;收入对具备该收入的人数作图。与肖克莱相反,罗托卡(A. J. Lotka)在科学出版物中观察到反幂律特性,因为他采取了大量的样本。
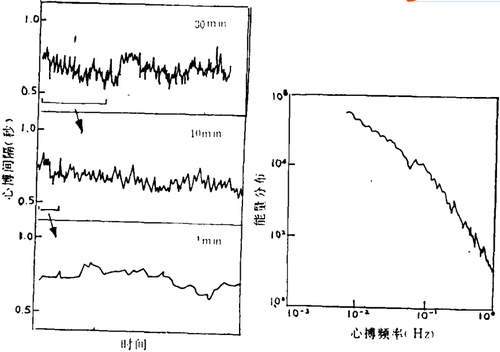
复杂过程一般具有关联时间(也叫弛豫时间)分布,它随关联时间本身作相反地变化,麦克卢帕(S. Machlup)强调1/t分布(t是关联时间)反映这样的事实:大自然“以公正的尺度控制……的大量机制是足够混沌的”。不足为奇,反幂律谱还表示一类明显不相关的生理过程。我们来考察心动过程(图3)。在正常条件下,心搏被普遍设想成遵循有序的、周期性的模式,这隐含在“规则的窦节律”的临床用语中。但是,分析健康个体的心率涨落,展现出令人惊讶的无规模式。而且,这些无规涨落在多种时间间隔中出现(图4)。对这种可变性进行谱分析,显示出具有相对宽泛频率范围的宽带分布,即1/f分布。
图4. 由反幂律决定的系统的复杂性,蕴涵着尺度不变性;即对此现象的描述在许多尺度上相似。这可由心搏频率的无规涨落来说明。左图显示可变性在三个尺度上相似。的确不能由其中一幅图来确定该尺度。右图可见心搏频率的整个分布满足近似为一直线的反幂律。
反幂律谱的这项研究表明,在多种时间尺度上产生自相似涨落的心搏可变性的调节中,可能包含有分形机制。目前在许多生理系统中,尺度的多样性可能取自用心电图和脑电图记录的时间序列测量。在解剖学中,结构的丰富性展现出内在的分形网络,说明分形几何学能为理解生理学提供一个新的基础。
声学中的噪声
分形之父曼德布劳特(P. B. Mandelbrot)提出一个用声音使这种自相似时间序列具体化的方法。若录下小提琴拉出的音乐并以不同速度放音,则有特色的小提琴声失真或消失,这说明小提琴声具有特征 ~ 间尺度 · 另一方面,当以不同速度放音时,存在一种音质没有感觉得到的变化的声音。这种声音'叫“尺度噪声”,加登纳(M. Gardner)评述过它。
尺度噪声最简单的例子是白噪声(一种无特色的杂音),宛如流水的声音,当以任一速度放音时它是单调乏味的。白噪声也就是收音机上广播电台之间听到的沙沙声,以及电视机无输入时荧屏上见到的 “ 雪花”。白噪声具有这样的性质,即任一时刻的涨落与其它任何时刻的涨落无关;也就是关联函数为0。全然不同的尺度噪声的例子是布朗噪声,其涨落在其特征时间尺度上强烈相关。白噪声的频谱与f无关,而布朗噪声的频谱由1/f2界定。
沃斯(R. K. Voss)和克拉克(J. Clark)在1978年研究了一种产生他们称为“随机音乐”(stochastic music)的算法,其放音音调随机选择,由规定的分布函数确定使用的特定音调的频率,“白音乐”(white music)由白噪声产生,听起来完全无规律,这是预料之中的,因为音调之间缺乏关联。“布朗音乐”由布朗噪音产生,听起来则很不同,因为音调之间相互关联,尽管布朗音乐比白音乐较有规律,然而它缺少自发性,传统音乐的审美要求显然需要某种自发性。
传统音乐证明是1/f现象的又一个例子。音乐的1/f谱在不相关的白音乐(具有平坦的谱)和布朗音乐(具有陡峭的谱)之间中途下降为1/f2谱。这是一个有关随机音乐的更奇妙的结果,实际上对古典音乐和爵士音乐进行分析,两者均表现出一个潜在变化的1/f谱。因此,尺度噪声反映了音乐的一个重要特征,比如巴赫等创作的音乐都显示出共享这个无处不在的1/f性态。
看来1/f噪声更具有艺术感染力。马夏(T. Musha)发现1/f噪声对生物系统其它方面的影响;例如,它在减轻长期难消除的疼痛方面起重要作用,经皮的电神经刺激是有益的,这种疗法有若上溯到公元46年的历史,早在1855,年便用于临床。最近的实验比较了此疗法中各种无规刺激谱的用途。白噪声刺激(如白音乐)看来太无规,偶而引起患者可怕的反应。1/ f2谱(如布朗音乐)看来太单调,使病人不快。在大多数情况中,1/f噪声备受偏爱,即使在刺激停止后很长时期内,它仍可减轻由创伤、癌症、腰部风湿痛和背痛等引起的疼痛程度。
广义噪声
许多现象可归为尺度不变性噪声,它具有由l/fα规定的通用谱形式。我们已述及在声学领域的三种情况:α=0(白噪声),α=1(1/f噪声)和α=2(布朗噪声)。然而,由于内在的过程并未具有一特征尺度,故存在一个α值的连续值域。为了有助于理解这个事实,回想在独立变量的大范围中,分布可为标准型分布(如正态分布或对数正态分布),其后在总数的最后少许分布百分数中经历一反幂律的转变。
回到图1,我们注意到占总数5多到97%的收入水平具有对数正态分布,它与反幂律分布重合。帕莱托(V. Pareto)在1897年就提出这个幂律性态。他收集了许多国家在历史上不同时期,个人收入和财产的统计资料。当它出现在宽阔的中心区域时,比例作用'定律适用于我们挣钱的手段,而最后2%或3%的人证明实行某种不同的方式。富人通过某种放大过程(如不动产投机)往往积聚额外的财富。这种投资的普遍特点是,仅以小差额支付的形式冒险使用来得容易的金钱,比如以承诺的10%支付随后的余额,组织某些投机商品,若商品的价格翻番,则10%的差额支付放大成9倍的利润。
这种倍增放大过程受通常所说的“统计杠杆原理”的支配。在一个或更多资深科学家的指导下,通过使用研究生和博士后,可以影响科学论文的发表。后者受惠于对多个出版物的合作关系,较他们单独工作可能产出的要多,而前者获益于经验丰富的“老将”的指导。因此我们通过测定科学家发表的论文数,在描述其产出能力时,预期有一个从对数正态到1/fα的转变。事实上确实观察到这个转变。它是Lotka在1926年发现的。
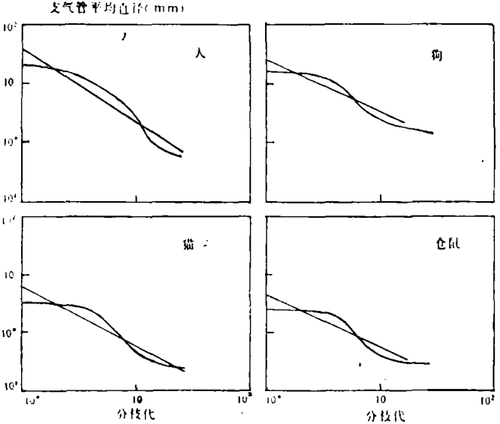
在生物学领域也能见到统计杠杆原理,例如,人肺便是具备两个主要特点(组织结构的无规性和丰富性)的生物复杂性的范例。这两个特征要求完成肺的气体交换功能。当支气管树分叉时,支气管的尺寸渐小。在各代均未支配时,分形尺度关系规定了一类管的大小。肺构造的经典指数模型忽视了各代支气管尺寸的可变性,对管直径仅采用平均值,而分形模型意味着一个“无限”系列的尺度对结构起作用,其中每个尺度因子小于其“邻居”,但各尺度因子具有比其“邻居”小的概率。第ζ代的平均直径由r(ζ)=A(ζ)/ζD给出,这里B是与支气管直径的可变性有关的分维,A(ζ)为一周期函数。因而肺的分形模型满足由周期性变化调节的反幂律关系。
拉伯(0. G. Raabe)及其同事的解剖学数据,说明肺的分形模型的适当性(图5)。在这个对数图中,反幂律关系表现为具有负斜率的一条直线。4组数据的主要特性都满足一条直线,但在直线附近具有明显的波浪起伏,正如分形模型所预言的,这种起伏起因于在反幂律回归线附近的谐波变化。这个特征在4个不同物种中出现,说明大自然在经典尺度生成这些物种期间,更偏爱分形结构。这可能与分形结构和过程拥有的差错耐受性有关。分形过程对内部的变化和外环境的变化更加适应。在生物结构中,大自然或许正是依靠这种涨落耐受性而进行选择的。
图5. 肺支气管直径总数遵循反幂律以及谐波变化。图中所示数据对应于4种动物,它们均近似为一条直线,同时在该线附近起伏变动。
我们认为在要求完整描述系统状态细节的程度上,复杂性具有其起源。描述在宽深的、缓慢流动的山涧中平静稳定的水流,只需极少的变量。然而,当小涧床变窄时,它越过和绕过岩石流动,则描述在最终的回水中涡流大小和时间尺度的谱,需要大量的细节,的确,想要完全描述溪流的混沌行为,需要无数个变量。囊括无数变量的不切实际性,驱使科学家在描述中引入概率分布。用这种方式还引入了一种重要的不确定性,它涉及空时定位和特定流元或涡流结构的速度。
概率描述的明显好处是,它不需要完全确定流场的演化;即人们不用预测出现特定涡流或时间尺度。更确切地说,人们只要满足于了解此事件出现的概率即可。眯眼观看奔腾水流的模糊图景,观察者对水流众多可能的未来状态或许留下深刻印象。这种湍流类似于我们上文讨论过的社会生物学过程,因为它也是1/f现象,并且具有α等于5/3的1/fα空间频谱。
正如我们所见,社会生物科学中大量系统的描述具有反幂律长尾,说明有意义的过程中缺少一个基本尺度。我们已经描述了取自社会学(Lotka定律)、经济学(Pareto定律)、语言学(Zipf定律)和生理学的实例。显然,重要的是以这些分布为基础的新尺度概念的潜在的社会学和生物学意义。例如,健康被理解为有序和可变性之间的一种平衡。某种疾病可能与正常分形过程的破坏(即与分形结构和功能有关的可变性受损)有关。健康人可变性的减少,反映在频谱的窄化上——“谱储备”的损耗。在最严格的病理情况中,可变性的损失最终会导致高度周期性和可预言行为的出现,医学文献充满了“病理周期性”的例子,人们应深思已知的生物医学过程的分形本质如何指导21世纪医学的发展——更不必说由具备尺度不变性的法律所规定的社会制度的宽广谱。
[American Scientist,1990年1 ~ 2月]