混沌理论揭示出一种支配现实世界正常运行的崭新的“测不准原理”,并且解释了时间为何只沿一个方向流逝。
时间的本质不仅对了解我们周围的世界(包括宇宙创生和演化的物理规律)至关重要,而且对诸如科学、文化和人类知觉之间的关系等问题有着不容忽视的影响。遗憾的是科学家们仍然没有一个易于理解的时间的定义。
问题在于,在日常生活中时间总是沿一个方向消逝——它存在一个箭头。人走茶凉,雪人融化,莽汉闯祸,我们未见有相反的过程,时间这样的无情流逝为热力学(不可逆过程的科学)所反映,而热力学被认为比宇宙的基本法则——由牛顿力学和量子力学给出的运动定律——还要基本。表征这些定律的方程对过去和未来不加区分。时间表现为一个没有箭头的可逆量。
显然,不可逆的热力学定律与可逆的力学运动定律两者互有抵牾。我们是不得已而放弃时间箭头概念呢,还是必须改变基本的动力学定律?如今,混沌理论会有助于回答这个问题。
爱丁顿(Arthur Eddington)曾说过,热力学第二定律是“自然界至高无上的法则”。这一定律来自这样一个简单的观测结果:在任何宏观机械过程中,某些或全部能量总是耗散为热。就像搓手发热一样。1850年,当德国物理学家克劳修斯(Rodolf Clausius)首先注意到这一司空见惯现象的深远意义时,他引入“熵”的概念代表因热耗散而缓慢增大的一个量。由于热量是组成系统的单个粒子无规运动的宏观表现,所以熵就被视为系统无序程度的量度。熵提供了一种把微观世界(其中牛顿力学和量子力学起支配作用)与宏观的热力学定律沟通起来的方式,
对于孤立系统(与环境既无能量交换,也无物质交换)来说,熵持续增长直至达到其最大值,即所谓的热力学平衡。这是系统的终态,此时密度、压强等宏观性质均与时间无关。平衡概念已证明对热力学有很大意义。结果不幸的是,我们不久将看到,虽然存在相当大的局限性,大多数科学家仍然仅在平衡态意义上讨论热力学和熵。
绝对孤立的系统是罕有的。更为常见的是“封闭”系统(与外界有能量交换但无物质交换)或“开放”系统(既有能量交换也有物质交换)。想象用活塞来压缩圆筒内的气体。气体与圆筒组成一封闭系统,故我们必须把系统与外界交换能量所产生的熵变以及气体内部的熵变都考虑进去。
传统的热力学描述方法如下。对于平衡态来说,系统和环境的总熵将处在最大值,如果气体及其环境在任一时刻均保持平衡,那么熵就不因气体体积的减小而变化,这个过程是可逆的。外界与气体的压强差在任一瞬时必须无限小,使平衡态得以保持,才能实现该过程,当然,实际上这种“准静态”压缩绝难实现,
因此,值得重视的结论是,平衡热力学不能描述变化,确切地说,通过平衡热力学无法了解时间。平衡热力学之所以深受物理学家和化学家的喜爱,是因为它易于数学化:它产生了描述一演化系统终末平衡态的量(比如熵)。熵就是通常所说的热力学“势”。
任何过程发生实际上总要经历有限的时间,从而必不可免偏离平衡。理论表明,系统只能趋近平衡,而不可能真实地达到。因此,热力学家们大多把注意力集中在热力学平衡这一特殊情况便颇具讽刺意味。平衡与非平衡两者的区别,恰如旅程与目的地或这句话的单词与末了的句点一般。正是通过不可逆的非平衡过程,系统才达到平衡态。生命本身就是一非平衡过程,因为衰老是不可逆转的。平衡等于死亡,同时腐烂的尸体分化为尘埃。
显而易见,当研究的系统因受外界影响而难以达到平衡(即系统与环境存在着连续的物质和能量交换)时,你必须应用非平衡热力学。“活”系统就是范例。
作为非平衡系统的一个例子,考虑起初其两端温度不同的一根铁棒。一般来说,若一端较另一端热,则沿该棒的温度梯度会使热端降温、冷端升温,直到棒温均一为止。这是平衡情形。但如果我们使一端维持在较高的温度,棒将受到一个连续的热力学“力”——温度梯度,这个力引起沿棒的热“流”(或热力学通量)。力与通量之积(即热流乘以温度梯度)给出棒的熵产生。
若系统是近平衡的,则通量以一简单、线性的方式依赖于力:力与通量成正比,这就是线性热力学,本世纪30年代耶鲁大学的翁萨格(Lars Onsager)奠定了它坚实的基础。平衡时力为零,通量亦为零。
普里戈金(Ilya Prigogine)率先用非平衡热力学来研究熵。1945年,对于近平衡系统他证明热力学势是系统的熵产生率;称之为“耗散”。普里戈金提出的最小熵产生原理预言,此种系统会演化为将耗散减至最低限度的一个定态。这使我们想起平衡热力学;终态是空间均匀的且不随时间改变。
远离平衡的系统
普里戈金的最小熵产生原理是一个重要的成果。后来他与格兰斯朵夫(Paul Glansdorff)及其他同事一道着手研究远离平衡的系统(其中力和通量的线性定律不成立),看看是否有可能将这一原理推广成对非线性远离平衡情形均成立的一般性判据。
20多年间,布鲁塞尔学派创立了著名的“广义热力学”理论(事实上这一术语该学派从未使用过)。为了把热力学原理运用于远离平衡问题,格兰斯朵夫和普里戈金假定该系统的性质就像一个平衡系统的良好的“拼凑物”,用这种方法使熵和其它热力学量如前一样依赖于诸如温度和压强这样的变量。
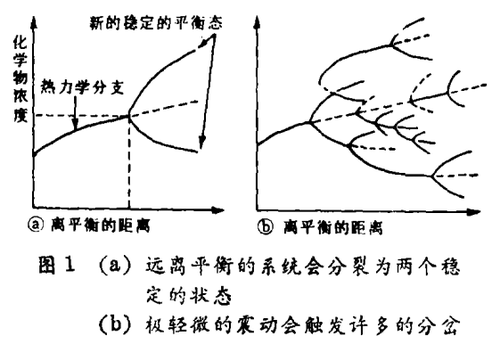
格兰斯朵夫 - 普里戈金判据对于远离平衡定态的稳定性给出了一般性表述:当它们受迫离平衡更远时会失稳,即它们将越过临界点或分岔点(系统在此处往往离开该定态)演化,并代之以另外的稳定状态(见图1a)。
—个重要的新情况是,在第一个临界点之外可能突然出现高度组织的状态。例如有的非平衡化学反应呈现规则的颜色变化——“化学钟”,有的则出现美丽的彩色旋涡。这些动力学状态与系统的最小熵产生无关,但所产生的熵被排入外环境。
因此,我们必须再三斟酌把时间箭头与向随机性匀速退化相联系——至少在局部水平,在时间之“终极”——平衡——随机性会笑得最后。但在较短的时间尺度内,我们能目睹有序结构脱颖而出,正如上而所说的,只要保持物质和能量流就存在这种结构。
由于有大量可能的行为可取得远离平衡,格兰斯朵夫 - 普里戈金判据并非不可逆演化的普适原理、非平衡系统随时间如何演化极其敏感地依赖于系统的微观性质——其组成原子和分子的运动,而与像温度、压强这样的大尺度参量近乎无关。在远离平衡时,微小的涨落会导致宏观尺度上的全新行为。难以计数的分岔会以随机的方式使系统跃入新的稳定状态(见图1b)。这些因时间或空间(或两者)而变的不均一组织结构,普里戈金称之为“耗散结构”;此种结构的自发演进叫做“自组织”。
现行的热力学理论不能阐明离开平衡之后在第一分岔点以外非平衡系统的行为。我们只通过在理论上考察该系统的动力学特性,来对此状态进行研究。为了描述该种非平衡系统的单向演化,我们必须构建基于方程的数学模型,这些方程表示系统的各种可观察性质随时间如何变化。按照热力学第二定律,这组刻划不可逆过程的方程总是含有时间箭头。
化学反应就是典型例子。当化学反应根据以微分方程形式表达的速率定律向热力学平衡方向进行时,我们能描述该反应进行的快慢程度。可以测定的量是所含化学物质的浓度及其随时间的变化率。
我们别指望在每个远离平衡的化学反应里6到自组织过程,但我们往往发现反应的内在机制导致非线性的微分方程,例如,当某一化学物质放大(或缩小)其产物时非线性出现,而且产生无法预测的复杂性。显然,就出现自组织结构(包括确定性混沌)而论,这种非线性是必要条件,但不是充分条件。本世纪50年代发现的著名的贝罗索夫 - 扎鲍廷斯基(Belousov - Zhabotinski)反应就是例证。
如今,正像本混沌系列文章所充分展示的,众多科学家都在用非线性动力学来模拟五彩缤纷的复杂现象——从流体动力学、化学和生物化学过程,到遗传变异、心脏搏动、种群动力学、进化论甚至经济学。所有这些不同现象的两个共同特征是不可逆性和非线性。确定性混沌只是一个可能的结果;另一个是更为规则的自组织;实际上,混沌是其中存在有序过载的一种特殊且很有趣的自组织形式。
我们可以再问:隐匿在热力学第二定律内部的不可逆性的起源是什么?传统的还原论观点认为,我们应该对可逆的力学运动方程的基础寻求诠释。但是,正如物理学家玻尔兹曼(Ludwig Boltzmann)所发现的,不可能把时间箭头直接建立在忽略它的方程之上。他试图使微观力学和第二定律和谐一致的努力以失败告终,从而产生本文开头提到的“不讨逆性佯谬。”
从组成系统(比如气体)的单个粒子的运动方程(不论是经典力学方程还是量子力学方程)出发,是推导在非平衡热力学中应用的方程的标准方法。由于我们无法知道每个粒子精确的位置和速度,我们只好转向概率论——统计方法——以把各个粒子的平均性态与整个系统的总体行为关联起来,此即所谓的统计力学。研究工作因所含粒子数极为庞大(达1024数量级)而获成功。
采用概率方法的原因不仅是由于无法测定有关粒子初始位置和速度的实际困难,量子力学预言这些局限是因为海森堡(Heisenberg)测不准原理的缘故,而且对于相当不稳定的混沌的经典动力学系统来说亦是如此。在去年珀西瓦尔(Ian Percival)的文章(“混沌:对于现实世界的一门科学”,译文见本刊1990年第6期)中,他阐释了混沌系统的一个显著特征是对初始条件的敏感性:系统的行为因不同的初始条件(不管它们怎样相似)随时间推移呈指数发散。要想预卜未来,你必须以绝对无限的精度——无论是原理上还是实际上都不可能实现——测定初始条件。而且,这意味着我们甚至不得不依赖微观水平的几率描述。
混沌系统以引人注意的方式表现出不可逆性,我们应该探寻与之相关的一个“似熵量”(entropy - like quantity),因为正是熵反映变化和提供时间箭头。理论工作者已经在一类称为遍历系统(ergodic system)的动力学系统中取得巨大进展。遍历系统是指将经历与其能量相容的每个可能动力学状态的系统。遍历理论的基础是本世纪30年代由冯 · 诺伊曼(John von Neumann)、贝尔霍夫(George Birkhoff)、霍普夫(Eberhard Hopf)与哈尔姆斯(Paul Halmos)奠定的,新近由苏联数学家柯尔莫果洛夫(Andrei Kolmogorov),安诺索夫(Dmitrii Anosov)、阿诺德(Vladimir Arnold)和西奈(Yasha Sinai)所发展。他们的工作表明,在动力学系统内部存在一整套行为层次——有的简单,有的复杂,有的简单和复杂似非而是地同时兼备。
如同前面的关于混沌的文章所述,我们可以用“相图”(phase portraits)来显示遍历系统的行为,但在这种情况下,我们把系统的初始状态刻划为相空间中的点丛,而不是一个点。图2 a所示为一非遍历系统:丛在空间有限区域内以周期形式形态不变地运动,图2 b所示为一遍历系统:丛形态不变但漫游空间的所有区域。图2 c中的丛,体积不变地扩展覆盖于细纤维之上,像一滴墨水在水中弥散一般;最终它侵渗,空间的各区域。这是所谓刘维(Liouville)定理的结果。换言之,总概率必定守恒(和为1);丛的行为好似一不可压缩的流珠。这是一个“混合遍历流”的例子,当时间演化停止时它证明趋向热力学平衡。此种扩展就是动力学混沌的一种表现形式。丛扩展的原因是它所包含的所有轨线均相互指数地发散,故它只能出现于混沌动力学系统。
混合流仅仅是格外不稳定的、混沌的遍历动力学系统体系的一员。以柯尔莫果洛夫命名的K流尤为无规。K流的行为达到总体不可预测性的极点:它们具有这样的显著特性,亦即甚至无穷多次的先前测量也无法预测下一次测量的结局。
我的同事米斯拉(Baidyanath Misra)与普里戈金合作在这一类极度混沌的系统中发现了一个似熵量,它具有随时间增大的理想性质。混沌的K流特性广泛存在于从1盒子中3个台球组成的系统(正如1962年西奈的开拓性工作所表明的),到包含大量粒子(可视为硬球)的气体,其中粒子之间的碰撞决定系统的动力学特性。许多理论工作者相信,日常生活中发现的大多数系统也是K流,尽管这一点尚未得到证实。我的同事赫里奥特 - 瓦特(Heriot - Watt)大学的彭罗斯(Oliver Penrose)和我正在尝试用严格的数学方法证明,对于该系统我们是否能用玻尔兹旻早先提出的方法来建立精确的动力学方程。
在与卡里奇(Maurice Courbage,也在布鲁塞尔)的合作研究中,就与不可逆性一致的K流而言,米斯拉和普里戈金发现了一个新的时间定义。这一称为“内部时间”(internal time)的量表示动力学系统的“年龄”。对于同样的系统在受牛顿方程约束的描述仅仅刻划可逆的动力学特征的时候,你可以把该年龄看作系统不可逆热力学属性的反映。
热力学和力学互相冲突已经一个世纪有余,然而现在我们展示了一种非常引人的联系。正像量子力学中的测不准原理(精确地已知粒子的位置就无法精确地获知其动量,反之亦然)一样,我们现在发现了一个新的适用于混沌动力学系统的测不准原理。这一新原理表明,系统热力学性质的完全确定(通过不可逆年龄的知识)使得可逆的动力学描述毫无意义,而动力学描述的完全确定同样使热力学图像失去效用。
研究动力学混沌有助于我们深化对熵概念的认识。熵原来是不稳定动力学系统的一个属性,正因如此,几率和机会对策推翻并取代了备受青睐的决定论。可逆性和不可逆性仿佛是同一枚硬币的正反两面。物理学家通过量子力学已经认识到,世界的全部结构比我们的语言所能表达和我们的大脑所能理解的要纷繁复杂得多。还有许多深层问题有待探索,但至少我们已经起步。
[New Scientist,1990年9月29 日]