原则上讲，量子力学可以精确地描述化学反应，但目前已做过高精度计算的仅为两个最简单最基本的化学反应，即：H+H₂→H₂+H和其同位素反应D+H₂→DH+H，理论计算必须要有相应的实验来检验，但这种实验的难度丝毫不亚于理论计算，这是由于检测H₂和产生具有精确能量值的原子束都不是件容易事。然而，斯坦福大学狄克 · 扎厄（Dick Zare）的研究小组，运用先进的激光技术，已攻克了这一难关，根据他们在《化学物理快报》上的论文，理论预测和实验结果相当一致。

如何搞清化学反应的细节，这一直是化学领域的主要课题之一，随着实验和分析技术的改进，现在已能够相当详尽地探测到分子反应碰撞的细节，对反应物和产物，选择其单个振动转动量子态进行研究也已成为现实。

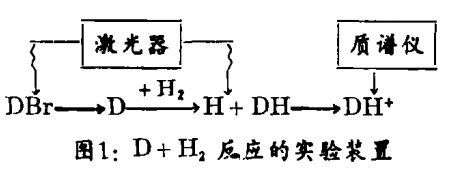
在斯坦福的这项新实验中，研究者采用了这一领域中一些熟知的方法（如图）用激光束离解DBr分子以产生快速的D原子束，然后再和H₂反应，生成DH分子，用同样的激光束将产物离子化再通过质谱仪，根据离子化的分子在质谱仪中的运行时间可计算其动能，这样扎厄和他的同事们就能推测出产物DH分子在不同振动 - 转动量子态的分布，他们发现，DH分子的最可n分布是在振动量子数j=4的九个转动态中，这一结果和量子力学计算取得了惊人的一致，在此同时，通过比较表明，经典力学的计算结果对DH产物转动能的预计略为偏高。

微观反应动力学的量子力学计算主要包括两个步骤，第一步是计算势能面，将体系的电子能表述为原子间距离的函数，目前量子化学从头计算法的巨大进展使得高精度计算H+H₂反应势能面成为现实。第二步是解出了原子在这一势场中运动的薛定谔方程。这种原子散射计算的通用方法是在近年来刚发展起来的。

回顾1976年，G. 沙茨（George Schatz）和A库柏曼（Aron Kuppermann）发表了具有里程碑意义的文章，在加州理工学院，他们采用近视的势能面，对低碰撞情况下的H+H₂→H₂+H反应作了计算，得到了较为一致的结果，计算表明，在室温下约有70%的反应是通过量子隧道效应进行的，由此表明许多能量不足以越过势垒的分子也能参加反应，作者充分利用反应体系的对称性，采用一组自然碰撞坐标来描述反应，尽管对这一反应的计算作了很大努力，但还不能够推广到D+H₂体系进行计算，因此有必要建立一种统一的理论方法。如运用极坐标，就可避免一些由自然碰撞坐标带来的困难，并将其计算方法推广到其它一些反应。

在此同时，一些研究者也独自发展了几种完全不同的理论方法，如伯克利的B. 米勒（Bill Miller），约翰 · 张（John Zhang），明尼苏达州的弗鲁拉（Don Fruhlar）和休斯顿的D. 库尼（Don Kouri）。他们研究的一些方法提供了有关反应D+H₂进一步深入的结果并和扎厄小组的实验相一致。这些理论借鉴了量子化学中分子轨道理论的一些思路，将反应物和产物的各个振动 - 转动量子态作为基组展开从而得到其计算结果，然而，只有运用大型的超级计算机如CRAY-2等，才能使这类计算成为可能。

目前有几种不同的实验方法，加州的J · 瓦伦丁（Jim Valentini）和他的同事们用了CARS（相干反斯托克斯拉曼谱）方法，运用两束激光，一束频率固定，另一束频率可调，用于检测产物分子，最初应用于D+H₂→HD+D反应，当时还没有精确的量子计算结果供对比，后来又应用于H+H₂→H₂+H反应，他们惊奇地发现，反应截面并不随着碰撞能的增加而平滑上升，这可能归因于“散射共振”，在某些碰撞能值时H原子的过渡态中有瞬间“陷阱”而造成这一现象，早些时候的理论计算也表明，当反应H+H₂严格限止在一维情况时，存在这种“共振”，但最近的计算表明，反应在三维情况下这种“共振”将被平均而不存在并且反应截面应随碰撞能平滑上升，如何解决理论和实验上的矛盾尚需进一步的实验来确证。

如何计算比H+ H₂更为复杂的化学反应？散射理论已被应用到H₂与O，F和Br原子的反应，但这需要更强大的计算机才能计算这些反应的势能面。有关H+H，反应的理论和实验为进一步的研究提供了基础，同时也说明了对于更复杂的化学反应，也能用量子力学方法进行精确描述。

[Nature，1990年4月12日]