一个寻常的分析错误会阻碍生物医学研究并误导公众。

2012年,《新英格兰医学杂志》刊登了一篇论文,声称吃巧克力可以提高认知功能。得出这一结论的根据是每个国家的诺贝尔奖得主数量与该国巧克力人均消费量具有强相关性。当我读到这篇论文时,我诧异于它竟然通过了同行评审,因为对我而言很显然作者犯了两个常见错误,这是我在生物医学文献中看到研究者进行相关分析时经常犯的错误。
相关性描述了两个观察现象之间的线性关系强度(为了简化说明,这里我着重阐述最常用的线性关系――皮尔森相关)。例如,一个变量值的增加,比如巧克力消费量,可能会跟随着另一个变量值的增加而增加,比如诺贝尔奖得主。或者可能是负相关:一个变量的增加会伴随另一个变量的减少。因为有可能两个数值不能用相同单位表示的变量关联起来――例如,人均收入和霍乱发病率――它们的关系是用一个无单位的数值来计算的,那就是相关系数。相关系数的数值范围是从-1到+1,绝对值越接近1,则表示相关性越强。
相关系数鲜明的简洁性隐藏了解释其意义时面临的相当大的复杂性。《新英格兰医学杂志》那篇论文的一个错误是,作者在群体数据的基础上得出关于个体的结论时,陷入了生态学谬误中。这个案例中,作者计算了集合层面(国家)的相关系数,然后错误地把这个数值用于得出关于个体层面的结论(吃巧克力提高认知功能)。实际上,个体层面的准确数据完全是未知的:没有人收集过诺贝尔奖得主吃过多少巧克力的数据,甚至于他们到底是否吃过。我并不是唯一一个注意到这个错误的人。化学家阿舒托什·乔伽莱卡(Ashutosh Jogalekar)在他的《科学美国人》博客《好奇的波函数》中写了一篇彻底的批判文章。加利福尼亚大学圣迭戈分校的比阿特丽斯·戈隆布(Beatrice A.Golomb)甚至与一个团队的合作者一起检验了这个假设,指出两个变量之间不存在相关性。
许多新闻机构不顾科学界的批评,报道了这篇论文的研究结果。论文从未被撤回,至今已经被引用23次。即使当错误的论文被撤回时,相关的新闻报道还保留在互联网上,还能继续传播错误信息。如果这些反映出对统计有所误解的错误结论甚至能出现在《新英格兰医学杂志》这样的著名期刊,那么我很好奇,这样的错误出现在生物医学文献中的总体频率有多大?
巧克力消费量和诺贝尔奖得主的例子把我引到了另一个更常见的曲解相关性分析的例子:即认为相关性就意味着因果关系的想法。计算出一个相关系数并不能解释一个数量一致性关系的性质,而只能评估这种一致性的强度。两个因素之间表现出一种关系,可能不是意味着它们之间相互影响,而是意味它们都被同一个隐藏的因素影响――在这个例子中,可能是一个国家的富裕程度影响了巧克力的消费量和高等教育的可获取性。相关性可以很肯定地指出一个可能存在的因果关系,但是并不足以证明存在这样的因果关系。
杰出的统计学家乔治·博克斯(George E.P.Box),在他的著作《实证模型的建立与响应面》中写道:“本质上而言,所有统计模型都是错误的,但是其中有一些是有用的。”所有统计模型都是使用数学概念对一个真实世界中的现象的描述,所以只是现实的一种简化。如果统计分析是精心设计的,与目前好的实践方针相一致,并且对所用方法的局限性有彻底的理解,那么,它们会非常有用。但是如果模型并不是按照上述两条原则设计的,那么它们不仅会不准确、毫无用处,而且还具有潜在的危险性――误导医生和公众。
我经常使用和设计数学模型来探究公共健康问题,尤其在健康技术评估中使用数学模型。为了这一目的,我使用已经发表的研究成果中的数据。不加批判地使用发表的数据来设计这些数学模型,可能会导致得出关于公共健康的不准确、完全无用,甚至更糟的是不安全的结论。
开始认识数据
在精心设计的实验中,相关性可以证实因果关系的存在。但是,在从非实验数据中得出因果推断之前,必须小心谨慎地使用统计模型。例如,加利福尼亚大学旧金山分校流行病学家史蒂芬·赫利(Stephen Hulley)及其同事发表的一个随机控制实验确定,激素替代疗法会导致心脏冠状动脉疾病的风险增加,尽管以前发表的非实验研究的结论是,激素替代疗法会降低心脏冠状动脉疾病的风险。这个精心设计的实验表明,非实验研究中低于心脏冠状动脉疾病平均概率的结果,是由那些使用激素治疗的人具有更高的平均社会经济地位带来的好处导致的,而不是由疗法本身导致。对非实验研究的重新分析,包括社会经济地位对收入的影响分析,得出了与随机控制实验相同的结果。但是损害已经造成:美国食品药品管理局顾问委员会已经批准激素替代疗法更换标签,允许把预防心脏疾病列为一个指示,这几乎是在上述实验十年之前。
即使科学家很清楚“相关性不等于因果关系”的真言,但是把相关性和因果关系混为一谈的研究在顶级期刊中还是太普遍。一篇被广泛讨论的1999年发表在《自然》杂志上的论文发现,两岁以下儿童的近视和睡眠期间夜间环境光曝光度这两者之间存在强相关。但是,2000年同样是发表在《自然》杂志上的另一项研究结果驳斥了上述发现,报告说儿童近视的原因是遗传性的,而不是环境因素造成的。这个新的研究发现父母近视与儿童近视之间存在强相关,指出近视的父母为孩子的卧室夜间开灯的可能性会更大。在这个例子中,作者基于假想的关联得出了一个结论,而没有检查其他可能的解释。但是正如下面的数据所显示的,完全无关的现象也可能会可笑地呈现出相关性。
除了相关性意味着因果关系这个错误的观念之外,我还看到了第三种相反类型的相关错误:认为相关性为零就意味着两个变量相互独立的想法。如果两个变量之间相互独立,例如,过去一个月我从早饭中摄入的热量与相同时期月亮表面的温度,那么我会预期这两个变量之间的线性相关系数为零。然而,反之则不一定总是如此。线性相关系数为零不一定意味着这两个变量之间是相互独立的。
尽管这个原则可以应用在很多例子中,仍然还是存在非单调的关系(想想一个上下波动的折线图),在这个例子中,相关系数的值为零并不意味着两个变量是相互独立的。为了更好地想象这个抽象概念,请想象一下按照下面的规则抛一枚不做假的硬币以确定投注金额:若第一次是正面朝上、第二次是反面朝上,则你输掉10美元;如果第一次是反面朝上、第二次是正面朝上,则你赢得20美元。如果我们定义X为投注金额、Y为净获胜金额,那么X和Y可能会是零相关,但是它们不是相互独立的――实际上,如果你知道X的值,那么你就知道Y的值。然而,这两个变量之间的关系可能是非线性的,因此无法通过一个线性相关检验来发现。
理想的情况是,科学家首先把数据绘制成图表以确定它是单调的(单调地上升或下降),但是从我在生物医学文献中看到的例子来判断,一些人正在偷工减料,并没有这么做。两个变量之间U型曲线的关系可能会有一个数值为零的线性相关系数,但是在这个例子中,并不意味着这两个变量是相互独立的。
1973年,英国统计学家弗兰克·安斯库姆(Frank Anscombe)发现了用图形展示这种误解的理想化的数据集,称为安斯库姆四重奏(Anscombe’s quartet),这个演示展示了统计特性非常相似的四组数据,每组数据的相关系数都是0.816。乍一看,每个例子中的变量看起来好像都是强相关。但是,只要观察一下这四组数据的图表,就足以意识到这个结论是错误的(参见上图)。只有第一个图表明显地显示出线性关系,对此做出强相关的阐释是合适的。第二个和第四个图表显示出两个变量之间的关系是非线性的,所以即使相关系数为0.816,这两个变量之间也不是相关的。第三个图表描述了几乎完美的线性关系,相关系数几乎为1,但是一个离群值把线性相关系数的值降低到了0.816。
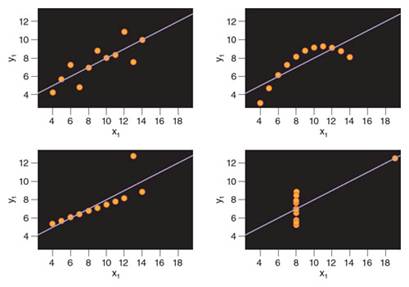
安斯库姆四重奏是4幅一组的数据图表,显示了相关系数为0.816的具有强相关性的数据。尽管统计上貌似显示出很强的线性相关关系,这样的结论却只适用于左上图,另外三幅图表都违反了统计分析的假设,由此强调了选择一个合适的数据分析之前首先绘制数据图表的重要性
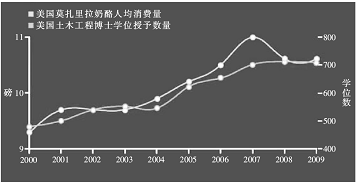
所有类型的不相关现象都可能具有相关性,包括莫扎里拉奶酪人均消费量与美国土木工程博士学位授予数量这两个风马牛不相及的现象之间。对伪相关性的错误阐释使得这种论文频繁地通过同行评审。
这种误解会对人类健康和政策产生重大影响。在对一种新物质进行安全性测试的时候,毒理学家通常以为高剂量的测试会比长周期、低剂量的测试更快、更不含糊地揭示低剂量效应。但是柏林夏洛特大学医学院的安德森·安德拉德(Anderson Andrade)及其同事的研究表明并非如此。他们在两种曝光程度相差很远的情况下,测试了一种名为邻苯二甲酸二辛酯(DEHP)的塑料成分和内分泌干扰物对老鼠的影响。在这个实验中,研究者监测了一种叫做芳香酶的关键的酶,它会诱导大脑的雄性化。他们表明低剂量的DEHP抑制了芳香酶,但是高剂量的DEHP确实增强了芳香酶的活性。
在安德拉德的研究中,这个剂量反应曲线遵循了非单调的模式,通常的高剂量测试预测不出这些低剂量效应。2010年,美国消费品安全委员会宣布可以认为含有DEHP的产品是有毒和危险的。像安德拉德这样的研究导致公众对用来设计激素活性化合物的毒理试验的基本假设产生了质疑,这个例子再一次证明了对数据的草率分析或是粗劣肤浅的阐释,一定不是一个良性现象。
避免错误
对相关性的所有三类错误阐释都可以避免。流行病学家和统计学家奥斯汀·布拉德福德·希尔(Austin Bradford Hill)在1965年表明,要得出因果关系的结论,就必须满足一定的判定标准。那些判定标准依然有效,但是科学家还研究出了从观察到的数据得出因果推论的更新的方法。还有一些方法正在研究中――例如,朱迪亚·珀尔(Judea Pearl)和詹姆斯·罗宾斯(James Robins)各自独立地介绍了一种从非实验研究中得出因果推论的新框架。罗宾斯研究出了一种统计解决方法,能把非实验数据转化为如同从一个随机控制实验中得出的数据。
为了避免生态学推论谬误,希尔建议那些缺乏个体层面的数据的研究者应该进行认真的多层面的数据建模。这种谬误通常会在流行病学研究中发生,当研究者只能获得集合数据时。在其1997年的著作《生态学推理问题的一种解决方法》中,哈佛大学的加里·金(Gary King)描述了导致这种错误的统计困难。正如金所解释的,用于生态学推论的数据往往具有庞大级别的异方差,这意味着一个数据集内部不同部分的差异性在很大的数值范围内波动。
集合数据通常比个体数据更容易得到,而且正确分析的话,会提供关于个体特性的宝贵线索,但是这还需要个体层面的数据。那么,就必须进行个体层面的建模,才有可能确定个体层面和集体层面数据之间的关联。只有到那时,才有可能得出集体层面的相关性是否适用于个体层面的结论。仅凭生态学数据,科学家是无法确定这类数据中是否可能存在生态学偏见;唯一的解决办法就是在生态学数据的基础上补充个体层面的数据。这种类型的建模通常涉及混合或多层次的统计模型,允许把个体数据嵌套到集合数据中。
为了避免因为相关系数为零就假定这两个变量是相互独立的,必须对数据进行绘图以确定数据是单调的。如果数据不单调,可以把其中一个变量或者两个变量都转换成单调的变量。在数据变换中,每一个变量的所有数值都使用同一个等式重新计算,这样能保持两个变量之间的关系,但是它们的分布改变了。不同的数据分布使用不同类型的数据变换。例如,对数变换压缩了大数值的间隔,扩大了小数值的间隔,当数组的平均值更大、变动也更大的情况下,这种数据变换是合适的。不获得原始数据,是不可能知道有没有犯这种错误的。
相关性错误和统计学本身一样古老,但是随着发表的论文和新期刊的数量不断增长,这样的错误也在倍增。尽管期望所有研究人员都对统计学方法有深入理解是不现实的,但是研究人员必须持续关注并不断扩展基本的统计学方法知识。不知道或是不加批判地评估所使用的统计学方法的充分性和局限性,通常是学术论文中所犯错误的根源。在一个研究团队中有生物统计学家和数学家的参与不再是一个优势而是必需。一些大学为研究者提供了选择,在把论文提交给出版机构评审之前,先让学校的统计学系检查他们的数据分析结果。尽管这个解决办法会对一些研究者起作用,但是让研究人员花费额外的时间这样做的激励几乎没有。
科学研究的过程要求足够的生物统计学知识,而这是一个不断变化的领域。为了达到这个目的,生物统计学家应该在一开始就参与课题研究,而不是等到测量、观察或是实验完成以后。另一方面,在批判性地评价发表的科学论文时,生物统计学的基本知识也是必需的。一个批判性的方法必须存在,不管论文发表在什么期刊上。在生物学研究中更谨慎地使用统计学,也有助于在其他领域设定更严格的标准。
为了避免这些问题,科学家必须清楚地表明他们理解了一个统计学分析背后的假设,并且用他们的方法解释:为了确定他们的数据集满足那些假设,他们做了哪些工作。如果一篇论文没有遵循这些最好的实践,那么就不应该让它通过评审。为了让论文评审者检验和重复论文中的数据分析,下面三个原则必须成为所有打算发表研究结果的作者的强制性规定:和论文一起附上原始数据作为补充信息,让评审者能充分获取用来分析数据的软件代码,并且在公开的在线数据库上登记研究结果、清晰地陈述开始研究之前设定的目标,强制提交总结结果以避免偏向于发表正面结果。即使当评审者有所疏漏的情况下,采取这些步骤也能加快发现错误的过程,增加了透明度,支撑了公众对科学的信心,最重要的是,避免了由于无心的错误而对公众健康造成损害的情况。
资料来源 American Scientist
责任编辑 彦 隐