2012年在大型强子对撞机上发现的希格斯玻色子证实了粒子物理学家长期以来的猜测:宇宙中存在一个场,可以产生大量的基本粒子。不幸的是,物理学家很难向他人解释,这个所谓的希格斯场是如何完成其艰巨任务的。
常见的方法是讲述一个荒诞的故事。以下是一个版本。
有一种物质,就像汤一样,充满了宇宙,这就是希格斯场。当粒子穿过它时,汤会减缓粒子的速度,这就是粒子获得质量的方式。
一些其他版本的类似故事将希格斯场描绘成类似蜜糖、灌木丛、人群或雪之类的东西。
然而,所有这些故事都与物理学家在大学一年级刚开始几周的课程中教授的内容相冲突。利用希格斯场施加阻力来产生质量,这违反了牛顿第一和第二运动定律。这种阻力如果存在,会在很久以前就导致地球螺旋式地进入太阳当中。此外,如果希格斯场真的是一种物质,它将被作为参照物,用来测量绝对运动,这违反了伽利略和爱因斯坦的相对论原理。
事实上,希格斯场与运动或减速无关。相反,它的故事都是与振动相联系的。
量子场论是现代粒子物理学的重要框架,根据这一理论,宇宙充满了场,包括电磁场、引力场和希格斯场。对于每个场,都有一种相应类型的粒子,我们最好将其理解为该场中的一点涟漪。电磁场的涟漪是光波,其中最温和的是光粒子,我们称之为光子。同样,电子是电场中的涟漪,希格斯玻色子是希格斯场中的最小涟漪。
一个静止的电子,就像吉他弦的振动一样,是一个驻波,以一个特定的频率振动,我们称之为共振频率。这种共振非常常见。因为弹拨的吉他弦总是以共振频率响起,所以它总是发出相同的音调。同样,摆锤的固定频率使其成为一个有效的时钟。根据同样的原理,每个静止的电子都以电场的共振频率振动。
如果你把钟摆放在非零的引力场中,一切都会改变。球笔直地垂下,如果受到干扰,就会摆动
宇宙中的大部分场都有共振频率。从某种意义上说,宇宙就像一件乐器,两者都具有最容易振动的特征频率。
对我个人来说,共振是世界的基础这一事实是我的快乐和惊奇想法的源泉。作为一名业余音乐家和作曲家,我很早就了解钢琴、单簧管和吉他的内部运作。但当我还是一名研究生时,我惊讶地发现,宇宙的结构,甚至我自己的身体,都是基于类似的原理运作的。
然而,如果没有希格斯场,宇宙的这种神秘的音乐性是不可能存在的。
在量子场论中,量子物理学和爱因斯坦相对论的结合导致了共振频率与基本粒子质量之间的关键关系:静止粒子振动得越快,其质量就越大。没有共振频率的场对应于没有质量的粒子。这种粒子,包括电磁场的光子,永远不会静止。
虽然希格斯场的荒诞故事表明,质量是由蜜糖状物质减缓基本粒子的速度引起的,但事实是,更强的希格斯场使基本粒子以更高的频率振动,从而增加了它们的质量。因此,人们可能会将希格斯场视为一种宇宙硬化剂,其作用是加快其他场的共振频率。
一个场如何改变另一个场的频率?钟摆可以给我们提供一个简单的例子。
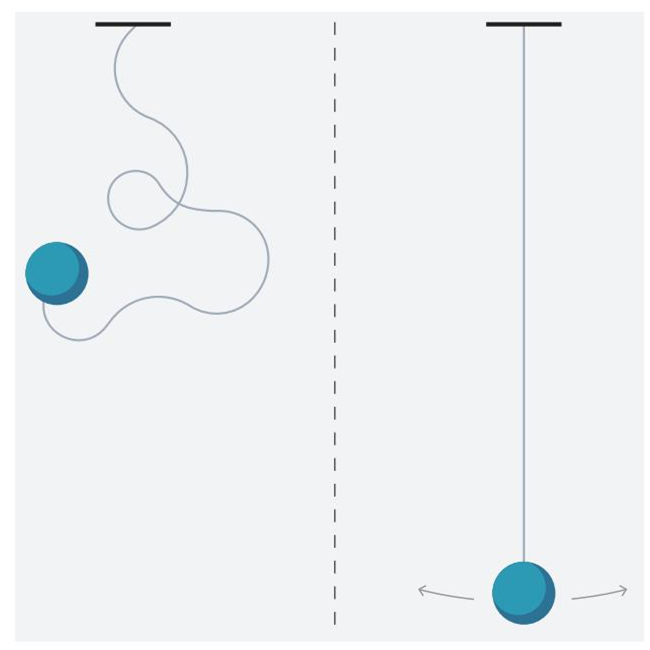
想象一下,把一个球放在深空中一段绳子的末端,那里的引力场基本上为零。球会漫无目的地漂浮。如果你稍微推一下,它可能会慢慢漂移,但不会振动。
然而,如果你把钟摆放在非零的引力场中,一切都会改变。球笔直地垂下,如果受到干扰,就会摆动。
当球静止时,它就处于平衡状态——稳定且平衡,没有理由移动。如果借外力让球向右移动,重力则会使它向左摆动,反之亦然。球的位置恢复到平衡点的趋势,即所谓的恢复效应,是导致它摆动的原因。
在这里,引力场起到了加强剂的作用:它使钟摆具有非零的共振频率。引力场越强,恢复效果越强,摆的共振频率越高。
类似地,希格斯场对其他基本场产生了恢复效应,从而改变了它们的振动方式。尽管任何场都可以像池塘中的波一样有移动的涟漪,但恢复效应同时允许场有静止的涟漪,即类似于吉他弦上的驻波。正如我之前提到的,这些驻波只不过是静止的基本粒子,在各自的场中荡漾。
这一概念是已故英国物理学家彼得? · ?希格斯(Peter Higgs,希格斯场因其命名)和他的学术竞争对手在20世纪60年代指出的核心观点:场可以使其他场变硬,从而允许它们的涟漪以共振频率在原地振动,赋予粒子以质量。大型强子对撞机对希格斯玻色子的实验研究证实,这确实是希格斯场的作用。通过使用粒子物理学标准模型的数学方法,即描述所有已知基本粒子和宇宙中的场之间相互作用的量子场论,科学家对希格斯玻色子的行为做出了与实验精确匹配的预测。毫无疑问:希格斯场对其他场产生了恢复效应。
因此,随着对希格斯场的深入理解,让我讲述一个不同的故事:
很久以前,宇宙诞生了。它炽热无比,到处都是基本粒子。其中有一个希格斯场,最初是封闭的。但随着宇宙的膨胀和冷却,希格斯场突然打开,具有了非零强度。当这种情况发生时,许多场变得僵硬,因此它们的粒子获得了共振频率和质量。这就是宇宙在希格斯场的影响下转变为今天的量子乐器的故事。
资料来源 Quanta Magazine
————————
本文作者马特?·斯特拉斯勒(Matt Strassler)是一位理论粒子物理学家。本文改编自物理学家马特?· 斯特拉斯勒的新书《不可能之海中的波浪》