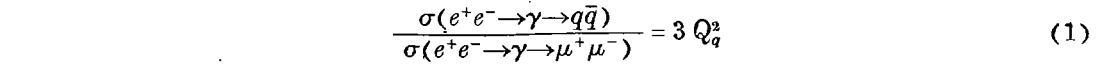(根据李政道教授1979年3月27日在上海市物理学会的演讲整理)
李政道教授来华访问期间,应上海市物理学会邀请在上海科学会堂作了“夸克模型——今日的粒子物理学”的学术报告。本刊特登载记录整理稿,以飨读者。此稿未经李政道教授审阅。文章中的小标题由本刊编辑部所加。
基本粒子概况
让我们来讨论一下目前基本粒子的概况。最近几年内,基本粒子有了很大的改变。从前我们认为基本粒子有以下几种,有光子,即光的电磁波的量子,它的质量等于零,自旋等于1。有万有引力子,即万有引力场的量子,它的质量等于零,自旋等于2。有轻子,英文叫Lepton,轻子有很多种,第一个是中微子,质量也是零,自旋是1/2;另外还有正负电子e±;其次是μ轻子,比电子重一些,它的电荷也是±1;再其次是最近三年内发现的τ±轻子,它的电荷也等于±1,比μ轻子重。在几年以前,我们认为除轻子外,基本粒子还有强作用的介子和重子,或称强子。但现在认为强子并不是基本粒子,基本粒子是夸克。夸克的种类分“上”(u)、“下”(d)、“奇”(s)、“粲”(c)、“底”(b)、“顶”(t)。这些夸克的质量,“上”和“下”差不多是零,“奇”差不多是100 Mev,即一亿电子伏,“粲”差不多是2 Gev,“底”差不多是5 Gev,顶还没有发现。我们认为所有的强子,像质子、中子、Λ粒子等等都是由夸克构成。这个概念讲起来很简单,就是所有的强子由夸克所构成,同分子是由原子构成一样,但有很大的差别。到目前为止还没有人看见过这些夸克。你会问没人看见过的东西是否在胡扯?因为夸克的质量是很低的,轻子已经量得非常精确,而单独存在的夸克还没有看见过。虽然有一些报告,如斯坦福大学的Fairbank(范尔朋克)说有实验表明有单独的夸克存在,但还未经其他的物理学家证明,只是个人说已经看见,科学上还不能被大家接受。所以我要给各位先讲一下,为什么近代物理学家觉得很熟悉的质子、中子、J/Ψ等等这一类粒子都不是基本的,而最基本的粒子只是左表所示的那些。
这些基本粒子造成了我们宇宙之间—切的东西。当然很可能未来的物理学会认为这些还不是最基本的,还有更基本的粒子。一层一层的,像层子那样,但是目前还没有到这种程度。现在用了这些假设的基本粒子就可以解释所有知道的现象。关键在于要说明,为什么我们觉得夸克是比质子和中子更为基本?为什么现在还没有看见他们单独存在?
夸克模型
先来简单介绍一下夸克模型。夸克模型就是说凡是具有强相互作用的介子与重子都是由夸克组成。夸克用q表示,英文中夸克是quark,是种起司蛋糕,是软软的,假如去德国或讲德语的瑞士,一定可以买到的。我们所讲的夸克不是起司蛋糕。在一部小说里有这么一句:“Three quarks for muster Mark”①。盖尔曼念了这句话觉得很生动,所以就叫它夸克。
夸克的电荷是分数
这样非常简单的想法,就产生了几个非常奇怪的结论,我先把这些奇怪的结论一个一个推出来,第一个结论是夸克的电荷是2/3或1/3。为方便起见,用Q表示电荷,取质子的电荷为1,这是一个电荷单位,正电子的电荷也是1,而电子的电荷是-1,这是一个方便的单位,用了这个单位,夸克的电荷是多少呢?Δ++的电荷是+2,它是三个上夸克组成的,自旋是平行的,这表示三个上夸克的电荷加起来等于2,因而上夸克的电荷,等于2/3。那么下夸克的电荷是多少呢?二上一下组成质子,电荷是1,所以下夸克的电荷是-1/3。我们再来看看对不对,π+介子是一个上夸克加一个反下夸克,因为下夸克的电荷是-1/3,所以反下夸克的电荷是-(-1/3)=1/3,相加起来等于1。这是对的。如此,用这样的方法,三个夸克组成重子,一个夸克、一个反夸克组成介子,我们就可推出夸克的电荷;上、下夸克的电荷分别是-1/3、2/3,也可以推出奇夸克的电荷是-1/3,粲夸克是2/3,底是-1/3,等等。可以用几百个重子来比一下子,这个结果可以解释所有重子的构造。故第一个惊人的结论是夸克的电荷是分数,不是整数。
这为什么惊人呢?因为我们还没有看见过一个东西,它的电荷是质子电荷的分数。根据普通的观念,凡是原子和分子都是由质子、中子和电子所构成的,中子的电荷是零,质子的电荷是1,所有原子核的电荷是整数,电子的电荷同质子的电荷值是一样,但差一个符号,是-1,所有原子的电荷,不管有多少电子都没有关系,都是个整数,由于所有的原子电荷是整数,所以所有的分子电荷也是整数,所以我们知道普通东西的电荷都是整数。怎么忽然来了个夸克,它的电荷是个分数?解释起来很简单,我们所知道的普通的东西都是由夸克 - 反夸克所组成的介子,或者三个夸克组成的重子,假如正反夸克、三个夸克的电荷加在一起就成为整数,这并不稀奇。不管怎样,第一个结论,夸克的电荷是分数。
夸克有三色,无色为强子
现在来看第二个非常惊人的结论。夸克的自旋等于1/2,凡是自旋等于1/2的粒子,我们都叫它费米子,费米子有一个统计法,叫做费米统计,按费米统计不能把两个完全一样的、自旋也一样的夸克放在一起。可是Δ++中三个夸克完全一样,这就违反了费米统计。这个矛盾在十几年前,有一个叫Greenberg(格林贝格)的作了解释。他说夸克还有颜色。我来解释一下,简单地说,他的意思就是说:“夸克有三色,无色为强子。”什么叫夸克有三色呢?Greenberg不会讲中文,这是我自己译的。其实每一个夸克都有三种,说它颜色也好,颜色只是个称呼,三种不同的夸克就很容易把它放在一块儿,这就不违反费米统计。你觉得它们是在同一状态,其实不然,它们是三种不同的东西,既然是三种不同的东西,当然可以具有相同的自旋。所以说“夸克有三色”。
但有个问题,假如夸克有三种颜色的话,你拿质子来将它变一变颜色,就会变出种种质子出来,颜色可以是红红黄,也可以是红黄蓝等等,随便你变,这一下子出来了很多种强子,但我们没有看见过。所以第二句话就说:“无色为强子”。既然强子没有颜色,就不会有许多种颜色的强子了。什么叫强子无色呢?这个看法是这样的,以介子为例,介子由夸克与反夸克组成,夸克的颜色与反夸克的颜色是相反的,所以,颜色都抵消了,整个介子当然就没有颜色。所以就只有一种无色的介子。另外重子里面有三个夸克,如何构成无色重子?可以想象颜色是个矢量,在颜色平面里,每一个夸克就像一个矢量一样(图1),把三个不同颜色的夸克放在一起,它的颜色的矢量和等于零。这就是所谓“无色为强子”。“夸克有三色”解释了它不违反费米统计;“无色为强子”保证了强子的种类不增加,所以夸克的种类虽增多,强子的种类与以前一样。
夸克质量很轻,强作用可以忽略
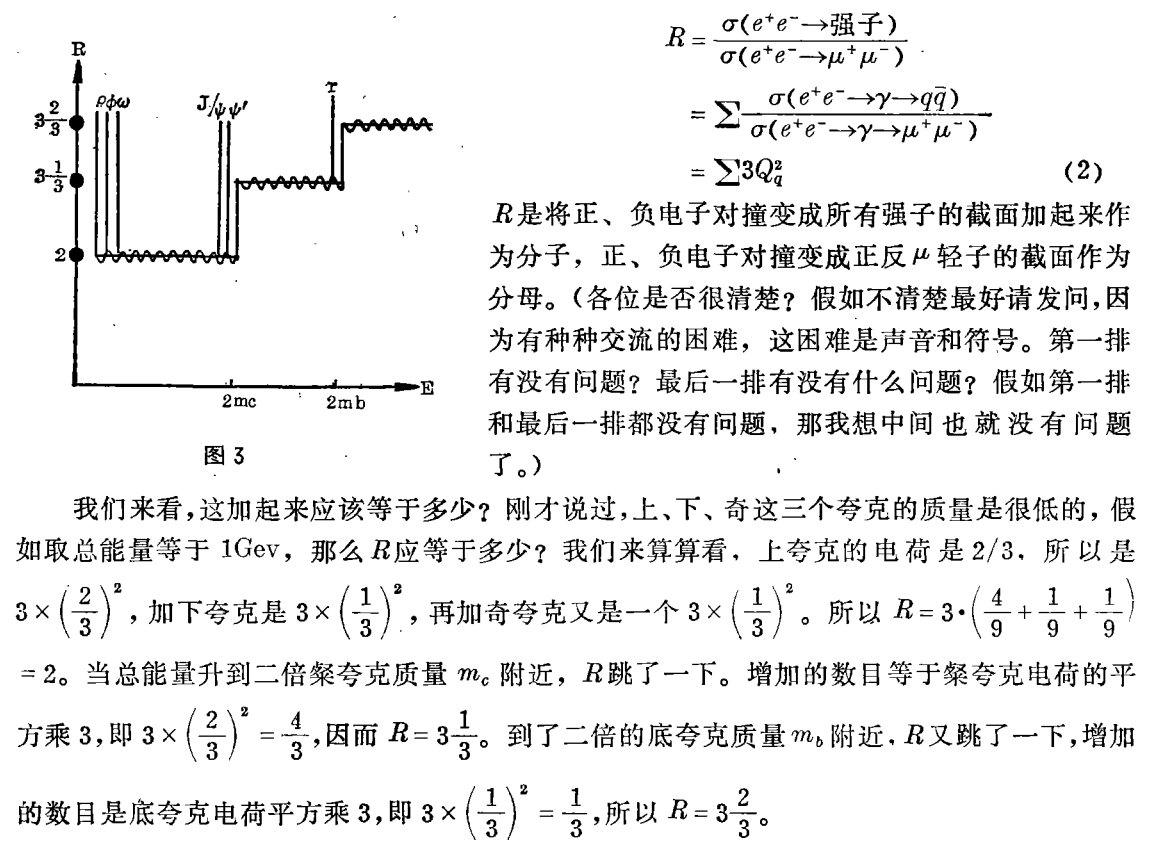
还有第三个结论。第三个结论就是说,夸克的质量是很轻的,它的强作用差不多可以忽略。把这三个结论合起来,就发现里面发生很大的矛盾,怎样解决这个矛盾呢?第三个是以直接实验的方法来测量夸克。怎样量呢?我们作两个假定,第一个是忽略夸克的强作用,这样就可以做以下的实验。(不作这样的假定也可以做以下的实验,只不过得不出以下的结论罢了。)这个实验现在做得相当确实的。把正电子与普通的电子对头撞一下,就变成了光子γ,接着γ产生或者是夸克与反夸克,也可以是正μ轻子与负μ轻子。(图2)假如忽略了夸克的强作用,这两个反应就可以同样处理,因为它们都没有强作用。μ轻子与电子没有强作用是原来就有的。而夸克没有强作用,则是我们的假定。这样图2中的二个图相比就完全一样,唯一的不同是电荷不一样,μ轻子电荷是1,而夸克的电荷是Qq。因此
(1)式中为什么是夸克电荷的平方呢?因为光子产生夸克与反夸克是跟电荷有关,电荷大振幅也大,电荷小振幅也小,这就是电荷的定义。振幅与电荷成正比,而几率是振幅的平方,所以(1)式中的分子是与夸克电荷的平方成正比,而分母上μ轻子的电荷是1,1的平方仍是1,所以(1)式也就与Qq2成正比。为什么有因子3,这是因为夸克有三色。由光子γ产生夸克时,产生这个颜色也产生另外的颜色,一共有三种,就有了个3。所以有了式子(1)就可以由实验来解释夸克的电荷以及夸克是否有三色。
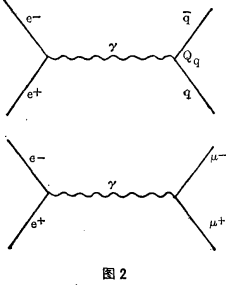
我们再来看实验的情况。以总能量E为横坐标,纵坐标用R来作图(见图3)。
假如实验是这样,那就证明了三件事情:第一证明了夸克的分数电荷;第二证明了夸克有三色;第三证明了夸克有质量,同时可以忽略夸克的强作用。这是个理论的推测,是不是有什么问题?实验的结果大致相符,但在图3中看到有一条条的直线,前面三条是ρ、φ、ω,中间二条是J/ψ和ψ′,最后的是γ。这就是说强作用不完全是可以忽略的。在跳跃的地方有峰出现,峰就是共振。所以我们就说存在峰的时候它的强作用不能忽略,但在峰以外这是可以的。因而我们刚才那样简单的解释是对的。的的确确,可能夸克的电荷是分数,是2/3,-1/3。夸克是有三色,而强子呢?“无色为强子”,所有的强子都没有颜色。夸克的质量mc ~ 2 Gev,mb ~ 5 Gev,并不怎么大。虽然并不能完全忽略夸克的强作用,不过在共振以外的地方是可以的。
这三点产生了极为严重的矛盾。这矛盾就是为什么我们看不见一个单独的夸克呢?既然夸克的电荷是1/3,或者是2/3,这个我们可以量的。既然夸克的强作用是不怎么大的,既然夸克的质量是不怎么高的,为什么它不跑出来呢?这个矛盾始终没有完全解决。今天,下面我们要讨论的是最近我自己在这方面做的一些工作,看看怎么样可以解决这个矛盾。
量子色动力学,红外发散与夸克禁闭的困难
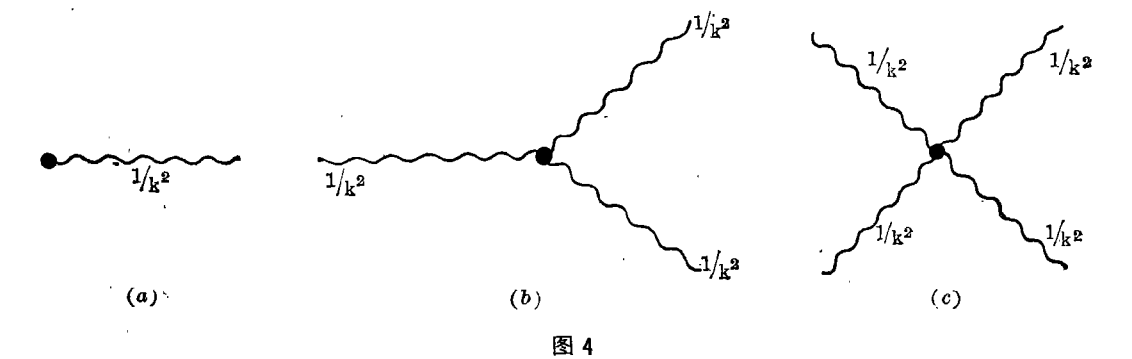
要解决这个矛盾,第一是要有量子色动力学。所以我先介绍一下量子色动力学,同时也说一下量子色动力学有什么困难?然后再看量子色动力学的困难加上夸克的困难,怎样可以消灭这些矛盾。夸克带有三色,色本身与电有点相似,我们就叫它色电。这色电也有一种介子,就跟光子传导普通的电磁场一样,我们叫它胶子,或是规范场,规范场是杨振宁很早在一九五四年介绍进来的。不过现在对规范场的看法跟那个时候有相当大的不同。规范场对于色,就等于普通的电磁场对于电荷一样,它们之间的关系是一样的,不过规范场跟色的关系更复杂。你看三种颜色加起来等于0,所以它的代数构造和电荷不一样,比如我们刚才讲过普通的电荷是1+1=2,1-1=0,可是色好像是一个矢量,有不同的方向,三个不同的色加起等于0。所以色的代数构造和电不一样。从技术上讲,电磁场是阿贝尔规范场,最早是由西欧的数学家阿贝尔提出的。1+1=2,1-1=0,1+1+1=0,是简单的代数。可颜色是复杂的代数,红+绿+蓝=0,三个加起来等于0,这当然是复杂一点了,这叫非阿贝尔规范场。它的复杂性就在于规范场自己跟自己有作用。这可用图表示,图4(a)表示普通的电磁场,电磁场跟电磁场并没有直接的作用,它可以通过电子而产生作用。通常一个电磁波跟一个电磁波,基本上是能彼此通过的。可是色规范场,因为它本身的几何变了,三个加起来等于0,它本身和本身就有相互作用。三个规范场有作用[图4(b)],四个也可以本身有作用[图4(c)]。这就有一个非常大的困难,所谓红外发散。什么叫红外发散呢,一个规范场的传播子是1/k2,k是波数。这就是说波数越小,传播子的力量越大。这样颜色也就有点像电磁场,在相当远的地方也有相当强度的力量,它与k的平方成反比。图4(b)把三个1/k2乘起来。图4(c)就把四个1/k2乘起来。红外的地方k→0,即波数很小,波长很大。波长越长,规范场自身的作用越大,k=0时,就成为无穷大,此即红外发散。这问题很难解决,在目前还没有完全解决。这是一个技术上,数学上的困难。另外有夸克禁闭的困难,夸克的概念很好,实验证明也很好,唯一的困难是我们没有看见过它,这是物理上困难。所以我们希望数学上的困难加上物理上的困难,也许可以克服掉这些困难。这也可以说是否定的否定吧!这在开始觉得很稀奇,让我来仔细地讲一下,我希望,这可能是对的。到目前为止这二个困难是大家承认的。以下来谈谈我自己做的工作。
真空作为理想的抗色电介质
第一步,把所有规范场放在一个大盒子里,长度是L,然后把整个宇宙放在这个盒子里,那就不应该有红外发散。因为k不能等于零,波长不能变为∞,波长最大只能等于L,是有限的,但最后我们还要使L→∞,这是数学上的一个技巧。这样做后,我来计算KL,KL是色电介常数。可以证明一个定理,这个定理是说,假如我们将同一个规范场放在大小不同的盒子里,那么,大盒子的色电介常数永远比小盒子的色电介常数小,即如果L>l,则有KL<Kl。这个定理现在没有时间来证明,但确是可以证明的,不光用微扰的方法是对的,而且当微扰展到任意高的阶数都是对的。这里要稍微用一些数学,可是也能正确地证明出来。电介常数本身没有绝对意义,比方我们就拿普通的电磁场来说,二个电子之间的力有多大呢?普通都晓得,电荷是e,距离是r的电子之间的力是(e2/r2)·(1/K),这里的K是电介质数。假定K对于真空是1,那么,式子就是e2/r2,这是为方便起见而假定的,电介常数是没有绝对意义的,可是相对的电介常数还是有意义的。普通在电磁学上我们假定电介常数对真空是等于1,这只是一个假定。这个基本道理是这样的,如取一个正电子,把他放在真空里,真空里面虽然没有电荷,但可以产生一对正电子和负电子,正电子把负的吸进一点,正的推出一点,这是普通的电动力学,叫做真空极化。这个真空极化的数值是可以量的,这是在三十几年前电动力学的一个很大的进步。将真空极化在理论上计算,实验上测量,这二个都很正确。也是说电荷在真空中是屏蔽的[图5(a)],如取正电子的话,由于真空极化,它的电荷就变得小一点。但色规范场就不一样,它是反屏蔽的[图5(b)],这是一个根本的不同,因为反屏蔽就会产生许多稀奇的现象。我一件件来解释一下,假如距离很小,l是等于质子的大小,为了方便取Kl=1,这纯粹是为了方便。而真正的宇宙、真正的真空L=∞,那么真空的K∞就一定比Kl小,这当然很明显是由那个定理推出来的。把一个电子放在真空里的话,它的电介常数就>1,为什么>1呢?因为它要产生屏蔽的极化电荷。可是现在产生了反屏蔽,所以它使得电介常数<1。反电屏蔽使电介常数减小,屏蔽是使电介常数增加。刚才这个定理就是证明了随便怎么样做的话,它都是反屏蔽的。其实这个证明很简单,只要你在微扰的时候,它是反屏蔽的,反屏蔽自身也产生极化,它是从同一符号反屏蔽产生更反屏蔽,更反屏蔽又更反屏蔽,所以它可以算到无穷高的阶数耦合常数都对。所以从物理上看,规范场有很特别的地方。
我现在把一个夸克放在真空中[图6(a)],真空等于一个介质,它的色电介常数是非常非常小的,等于零时则真空是个理想的抗色电介质。所以我们如果假设真空是理想的抗色电介质,那么就很容易了解,为什么夸克是被禁闭的?我们拿一个夸克来,由它形成的最低能量态叫孤立子(Soliton)。它里面KL=1,在外面K∞=0。我们来研究如图6(a)所示的物体,半径为r,D是电位移矢量,在内部因为KL=1,所以D内=E内。在外边K∞=0。另外由高斯定律可知D在垂直于分界面的方向上的分量是连续的,所以D外≠0。为什么?因为夸克有颜色,有颜色就等于像有电荷一样,有电荷则D在径向的分量就不为零。所以D在外边不能等于零,D外=K∞E外≠0。因为在外面K很小,所以E外就很大,这就使这个物体的质量很大。假如K在外边变成零,E外就成为无穷大,就把这个物体的质量变成无穷大。我再重复一下,这是个关键。假如真空是理想的抗色电介质,那么我放一个夸克在里面,夸克在它周围就产生一个洞,周围的D就不能等于零,D不等于零的话,外面的E外在K变成零的时候就变成无穷大,零乘无穷大变成有限的。E是无穷大,能量变成无穷大,就是夸克的质量变成无穷大。可是,假如我放一个夸克和一个反夸克在这里[图6(b)]。它的磁力线如图那样走,磁力线这样走使它在径向是等于零的,在径向等于零,就使五在外面可以是有限的。这就是说夸克和反夸克一起的质量不是无限的。关键就在这儿。所以,如果假定真空是等于一个理想的抗色电介质,我们就可以知道,有色的夸克它的质量等于无穷大,而无色的强子它的质量是有限的。我们可以更进一步来看,无色的强子内部和外部的构造到底怎么样?夸克在强子里面质量有限,如果你把这个夸克拿出来,那它的质量就变成无穷大,如真空是基本上理想的抗色电介质,那么夸克是有限重,不过很重很重,比强子重得很多,即夸克的禁闭是暂时性的,而不是永久性的。我们现在来研究超导,超导体是理想的抗磁体,它的磁化率μ=0。在色规范场中,真空是理想的抗色电介质,它的色电介常数K∞=0,这二者有一个相似的性质。超导体里面磁化率等于零,外面磁化率等于1。而强子里面K=1,外面K=0。两者相比,超导时的磁场在量子色动力学里变成色电场,磁化率变成它的色电介常数,把里面的变成外面的,把外面变成它的里面。我们再来看超导体,磁场只能在它的外面通过,不能穿透到里面去。而拿粒子来看,外面变里面,里面变外面,所以所有的色电场都弄到里面去,夸克就禁闭了。这就是说,夸克禁闭其实没有什么稀奇,它是最基本的物理的道理。对色规范场,来计算它的真空极化,跟电动力学恰好相反,它不是屏蔽的,而是反屏蔽的,它正的变成更正,既然正的变成更正,它这个屏蔽产生的极化色电荷,又产生自己的极化色电荷,正的变成更正,更正,更正。所以它的K变成更小更小更小,所以很容易可以想象,K可以变成非常小,而也许是等于零。假如说它非常小,有色的夸克D不能等于零。D不等于零的话,因为D=K∞E那E就变成很大,所以有色的夸克非常重,无色的强子变得很轻。这就是为什么无色为强子。强子普通说质量都不十分高,1 Gev到2 Gev。所以有色的质量就高,无色的质量就低。夸克有三色,无色为强子。夸克就因此而禁闭。这就将以前认为是基本粒子的质子、中子、J/ψ、Λ等不再认为是基本的了。而比较基本的只是光子,万有引力子,种种的轻子,就是中微子,正反电子,正反μ轻子,正反τ轻子以及夸克的上、下、奇、粲、底、顶。那么到底这些夸克,这些轻子是不是也是基本呢?我们目前的认识还没有达到这个水平,需要做更高能量的加速器,再钻到面里去,才可以一层一层地剥开来。就像层子的观念一样,它们有更基本的构造,不过我想今天的报告就到这里为止。
[上海市物理学会高能物理理论组、本刊编辑部整理]
————————
①“Three quarks for muster Mark。”詹姆士·乔伊斯(1882~1941)的《芬尼根的彻夜祭》中的一句。意为“为检阅者似的马克王,三声夸克!”夸克海鸟叫声。——整理者注