对任何平面地图着色,使得任何两个邻国都没有相同的颜色,只要四种颜色就够了。这个著名的猜测已经证明是真实的了,用的是一种依靠高速计算机的新的证明方法。
1852年,弗朗塞斯 · 古斯里(Francis Guthrie)在伦敦大学院①(University College London)完成学业之后几个月,写了一封信给他的兄弟弗雷赘克(Frederick),后者当时还在学院,是数学家沃嘎斯特斯 · 德 · 莫尔根(Augustus De Morgan)的学生。弗朗塞斯向弗雷赘克指出:看来,画在一张纸上的每幅地图都可以只用四种颜色着色,使得有共同边界的国家有不同的颜色,他问是否有什么办法在数学上证明这点,弗雷赘克不知道,去问德 · 莫尔根,他也不知道,在其后的124年间,古斯里的四色问题,即是证明每幅地图至多需要四种颜色的问题,或画一幅需要五种颜色的地图的问题,激起某些职业数学家、业余数学家以及高中学生们的强烈兴趣,因为这些人觉得,所有未被解决的问题之所以仍然没有解决,不过是老一代的无能而已。
1976年,我们解决了四色问题。古斯里猜测在数学上得到证明,但是证明的方式却同他本来指望的方式大不相同。甚至当代的数学家中,那些不知道产生这个证明的发展过程的人,也被我们的结果弄得相当惊讶,因为我们的证明前无古人地使用了计算机,而证明的计算部分使整个证明的长度超出了传统上可以接受的程度。实际上,证明的正确性不靠计算机是无法检验的。此外,这个证明的某些关键想法,是通过计算机试验而得以完善的。当然,四色定理的简短证明说不定有一天会找到,也许是一个聪明的高中学生找到的。但是,也可以想象,这样的证明是不可能出现的。在这种情况下,就出现了一种新颖而有趣的定理类型,即是这种定理不具有任何传统风格的证明。
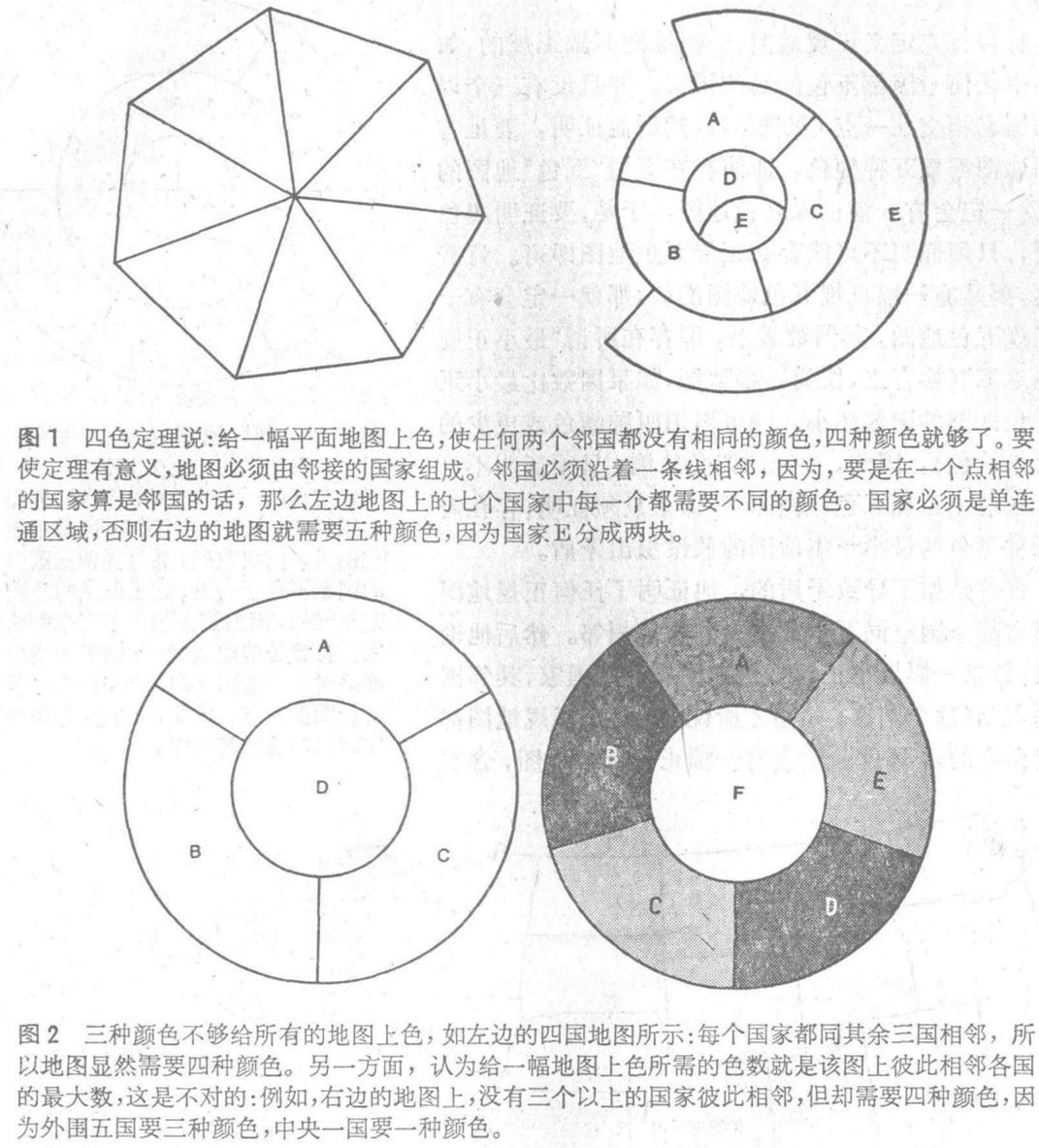
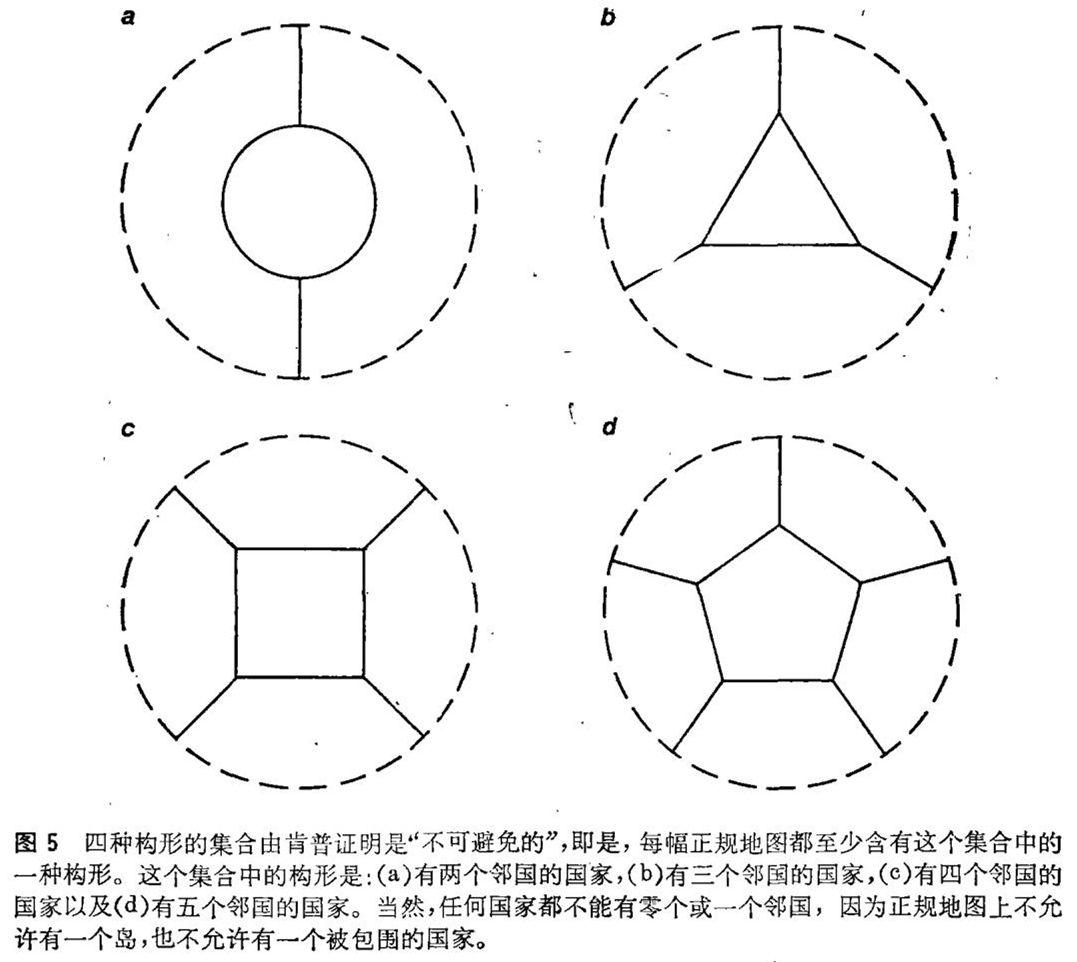
尽管本证明有其新奇的方面,但是四色问题以及基本证法,在数学上都是根深蒂固的。我们首先回到弗朗塞斯 · 古斯里的信中对问题的原始提法来加以考察。所谓“邻国”,古斯里必定是指沿着一条边界线相邻而不是在一个点相邻的国家;否则,一幅地图上的国家要是看起来像是一张馅饼分成的楔形块,那么有多少国家就需要多少种颜色,所谓“国家”,他肯定是指一个连通区域,因为,如果一个国家可以由不止一个区域组成,而这些区域是隔离的,那就不难作出一幅五国地图的例子,其中每个国家都同其余四国中每一国相邻(见图1)。
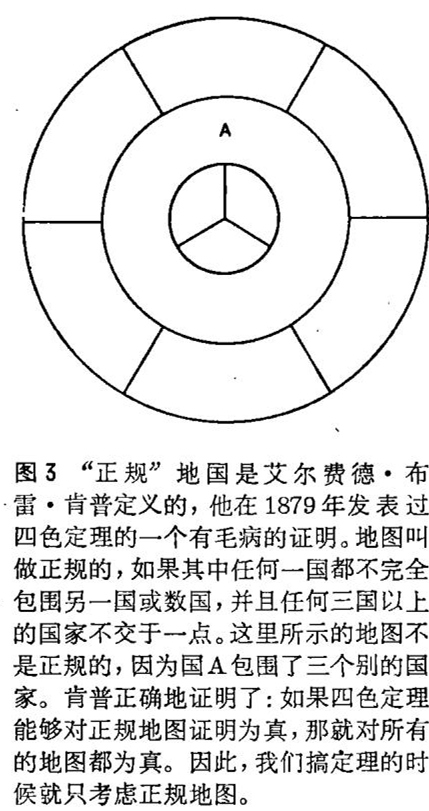
古斯里和德 · 莫尔根肯定认识到,可以画出一幅四国地图,使得每个国家都同其余三国相邻(见图2左图)。这样一幅地图需要四种颜色,因而三色猜测不真:要对所有的地图着色,三种颜色是不够的。
德 · 莫尔根证明了,不可能有五个国家处于这样一种位置,使得其中每个都同其余四个相邻,这就使他相信,决不需要五种颜色,因而四色猜测为真。可是,证明地图上不可能存在五个彼此相邻的国家,并不等于证明四色猜测(见图2)。许多业余数学家,不懂得这个事实,独立地发现了德 · 莫尔根的结果的证明,便自以为证明了四色猜测。
1878年,数学家阿瑟 · 凯利(Arthur Cayley)不能证明或推翻四色猜测,便把问题提到伦敦数学会。不到一年,一位律师兼数学会会员艾尔费德 · 布雷 · 肯普(Alfred Bray Kempe)发表一篇文章,声称证明四色猜测为真。肯普的论证极为巧妙;他的证明尽管是不完善的,但却包含着一个世纪以后产生正确证明的大部分基本想法。肯普试图用古典的归谬法的方法来证明猜测为真;他假定猜测不真(即至少有一幅地图需要五种颜色),然后去证明这个假定引出矛盾。得到矛盾就表明原来的假定(有一幅地图需要五种颜色)是错的,因而四色猜测(四种颜色就够了)为真。
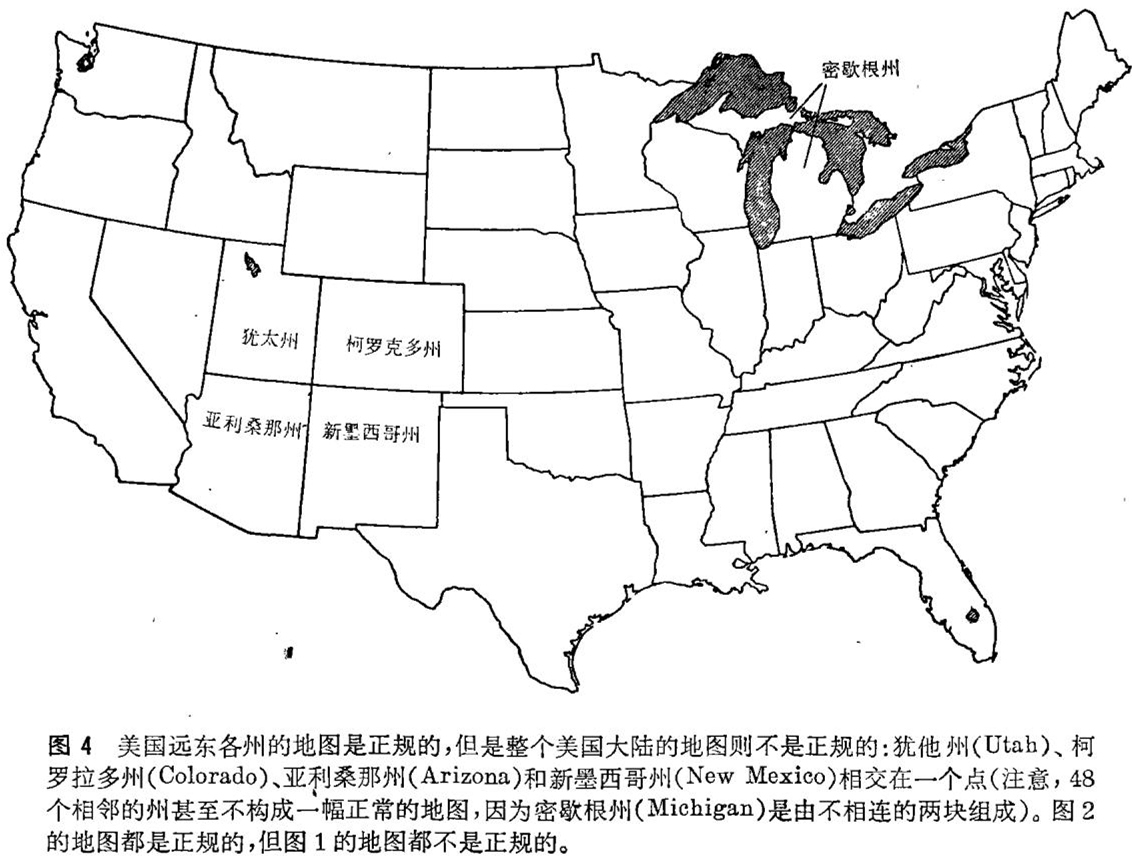
肯普首先定义正规地图:一幅地图叫做正规的,如果其中任何一国都不包围别的国家,并且没有三个以上的国家相交在一点(见图3)。然后他证明:要是有一幅地图需要五种颜色,即使存在所谓“五色”地图的话,就一定会有一幅正规五色地图。于是,要证明四色猜测,只需证明不可能存在正规五色地图即可。肯普指出:要是有一幅正规五色地图的话,那就一定会有一幅正规五色地圈,其国数最小,即存在所谓“最小正规五色地图”(换言之,任何一幅地图,如果国数比最小正规五色地图的国数还小,就可以用四种颜色或更少的颜色来着色)。因此,要证明四色猜测,只需证明不可能存在最小正规五色地图即可,即是只需证明:存在需要五种颜色的最小正规地图的假设引出矛盾。
肯普是如下导致矛盾的:他证明了任何正规地图上都有某个国家同五个或更少的国家相邻。然后他论证说:如果一幅最小正规五色地图有一个国家,其邻国不到六个(这个国家,如刚才所说,是任何正规地图都必定含有的),那就一定会有一幅正规五色地图,含有更少的国家。要是这个论证完全正确的话,是会产生矛盾。假定存在最小正规五色地图,肯普就会证明存在更小的正规五色地图;这就会同最小正规五色地图的定义矛盾。因此不可能存在最小正规五色地图,从而也就不存在任何五色地图,证明就完成了。肯普正确地证明了:最小正规五色地图上存在一个国家有两个、三个或四个邻国的情形将引起矛盾,但是他对五个邻国的情形的证明是有漏洞的。在我们对四色定理的证明中,我们考察了大约1500种国家分布的情况,从而纠正了肯普对最后一种情形的有漏洞的分析。肯普的证明在过去一百年间一直是数学家密切注意和精心改进的对象,我们的方法基本上是其有效部分的引申。
肯普证明了,在每幅正规地图上至少存在一个国家有两个、三个、四个或五个邻国(换言之,平面上不存在任何正规地图,使得每个国家都有六个或更多的邻国)。这可以表示为下述说法:由一个国家与两个国家相邻组成的“构形”、一国与三国相邻的构形、一国与四国相邻的构形、一国与五国相邻的构形所成的集合(见图5)是“不可避免的”,即是每幅正规地图必须至少含有这四种构形之一。不可避免性是我们证明四色定理的两个重要的基本思想之一。
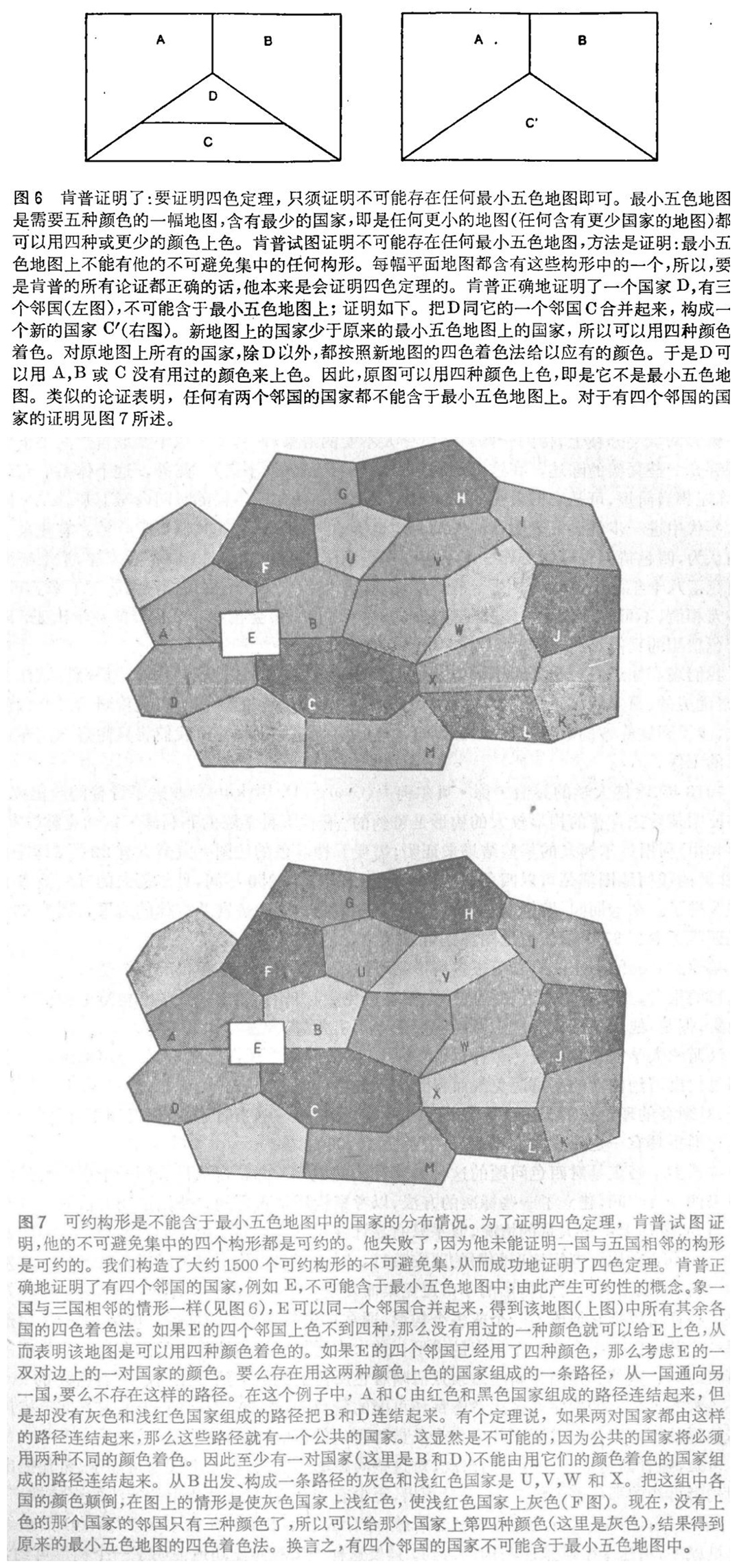
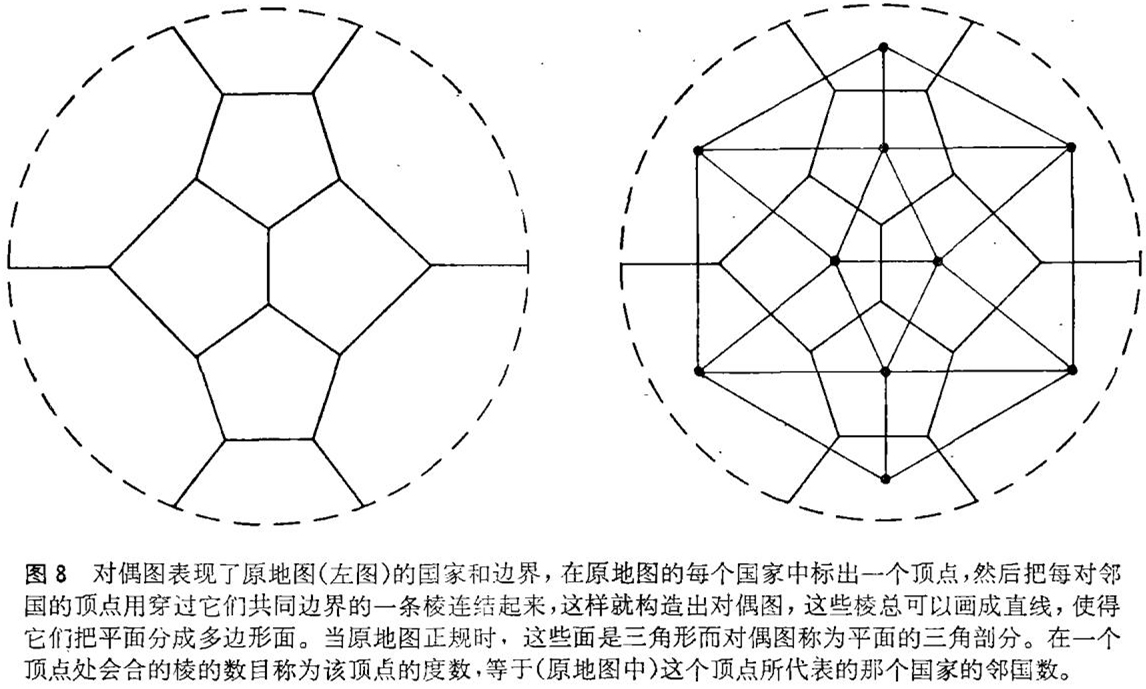
第二个重要的思想是可约性。直观上说来,一个构形是可约的,如果仅仅考察这个构形以及国家排列成链的方式,就能证明该构形不可能出现在最小五色地图上,肯普证明了他的四种构形中有三种是可约的,但是未能证明一国与五国相邻的构形是可约的。肯普证明了有四个邻国的国家不能出现在最小五色地图上,由此产生证明构形可约的方法。使用可约一词来源于肯普的论证形式:他证明了,如果一幅最小五色地图含有一个国家,比如说有四个邻国,那么就存在一幅五色地图,其国家数目减少(见图6及图7)。
我们可以说,肯普对四色猜测的进攻就是企图找出可约构形的不可避免集。找到这样一个集合就足以证明四色猜测了,因为,它表明,每幅地图都含有一个不可能含于最小五色地图的构形。因此,不能存在任何最小五色地图。从而如肯普所正确证明的,这就蕴涵着根本不存在任何五色地图。我们也像肯普那样,通过构造可约构形的不可避免集来进攻四色问题。可是,我们的不可避免集不是由四种简单构形组成,而是由大约1500个复杂的图形组成。
1890年,即肯普发表他的证明之后十一年,佩塞 · 约翰 · 赫伍德(Percy John Heawood)指出,肯普关于任何最小五色地图都不能含有一个有五个邻国的国家的论证是有毛病的,而且错误不像是容易修补的。赫伍德在他进攻这个问题时研究了原来的四色猜测的一种推广。古斯里和肯普研究的地图,是平面或球面上的地图。赫伍德考虑更复杂的曲面上的地图,能够得到一个优美的论证,对这些曲面上的地图着色所需的色数给出一个上界。要是他所用的方法可以应用于平面的话,本来是会给出四色猜测的一个证明的。
赫伍德继续不断地搞这个问题不下六十年。在这段时间里,许多其他的优秀数学家也对四色猜测付出了大量的劳动,人们也许会感到奇怪,为什么那么多的数学家把那样多的时间花在这么一个似乎没有什么实际意义的问题上。这个问题的答案在于:过去一个世纪来关于纯数学的性质作出了许多发现,而那些发现的结果却使数学家过分相信数学的威力了。
到19世纪末,数学家能够建立起一些强有力的理论,使他们能够解决许多困难的问题,从而使人感到,任何问题,只要能够用数学语言适当地提出来,就能够用充分有力的数学思想给以回答。而且,人们相信,回答这些问题的方式可以使力能胜任的数学家能够在适当长的时间内检验答案的正确性。四色猜测似乎就是这样的问题。数学家之所以未能解决这个问题,似乎显然是因为他们还没有建立起适当的数学工具的缘故。
可是,二十世纪三十年代的一些新发现,向十九世纪的数学完备的信念提出了挑战。库尔特 · 戈德尔(Kurt G?del)和阿隆佐 · 切尔奇(Alonzo Church)在形式逻辑这个最精确地提出证明概念的数学分支上,得到一些新奇而令人不安的结果;证明了在似乎是最自然的逻辑体系中却存在一些真实的陈述,在这个体系中无法证明为真(或不真)。此外,这个体系中有些定理,陈述相当简短,可是它的最短的证明也长得无法在任何适当长的时间内写下来。二十世纪五十年代中进一步的研究表明,同样的困难也影响到逻辑以外的其他数学分支。有些数学家开始认为,四色猜测也许就是那些既不能证明也不能推翻的论断之一。不管怎样,这个猜测已经研究了八十年而未能成功。另一些数学家觉得,即使有证明,也会长得无法写下来。可是,很多人相信,不可解瘟疫不可能蔓延到这个数学领域来,而会找到一个优美的数学论证,以决定四色猜测的真假。
我们现在知道有一个证明了,但是我们还不知道(也许永远也不知道),是否存在什么证明,是优美的、简明的而且是人类的数学智力所完全能够理解的。证明四色猜测的形形色色的尝试,涉及到这样多的数学领域,以致不可能在这里全部加以讨论。我们将只注意直接导致本证明的工作。
1913年,哈佛大学的乔治 · 德 · 贝尔柯夫(George D. Birkhoff)改进了肯普的约化技巧,能够证明某些比肯普的构形较大的构形是可约的。麻省工科学院的菲利浦 · 富兰克林(Philip Franklin)利用贝尔柯夫的某些结果来证明:需要五种颜色的地图必定至少有22国,即是,少于22国的任何地图都是可以四色着色的。在1913年至1950年间,贝尔柯夫的方法被许多数学家改了。在这期间,发掘出一些可约构形,主要是为了改进富兰克林的结果。到1950年,已经证明了少于36国的任何地图都是可以四色着色的。
虽然这方面的工作的确表明很多构形是可约的,但是到1950年已经证明是可约的所有那些构形的集合,甚至还不接近于构成一个不可避免集。只有二、三个数学家构造了构形的不可避免集,但是,他们的工作会产生可约构形的不可避免集,却没有什么希望。
汉诺威大学的赫恩瑞奇 · 希什(Heinrich Heesch)似乎是肯普之后,公开声称四色猜测可以通过找出可约构形的不可避免集而得到证明的第一个数学家。希什在1936年开始搞这个猜测,对现存的理论作了些重要的贡献。1950年,他估计,在(当时还是)假定的不可避免集中,可约构形将具有一定限度的大小,数目大约是10,000。
构形大小必定是对四色问题的这种处理方法的主要考虑。自从肯普第一个引进可约性思想以来的一百年间,建立了一些标准的方法,以考察构形是否可约。使用这些方法来证明大的构形可约,就需要考察大量的情况,似乎只有靠计算机才做得到。每个构形都被一圈邻国所包围;圈的大小,或构成围绕构形的圈的国家数目,对于证明该构形可约时碰到的困难有直接的影响。当人们试图构造可约构形的不可避免集而发现一个特殊的构形不可约时,为了得到好的效果,往往可以把它换成另一个或多个构形,通常是包围圈更大的构形。可是,把一个构形换成另一个其包围圈多含有一个顶点的构形,就大大增加了可约性检查的困难以及为此所需的计算机时间。这部分是因为新圈诸顶点清晰着色所需的色数大约是原圈诸顶点色数的三倍。此外,检查可约性的程序要多次考虑每种可能的着色法。1950年,计算上的困难似乎排斥了构造构形的不可避免集并证明其中每个成员都可约的可能性。
可是,随着高速数字计算机的出现,对这些问题的进攻,在技术上成为可能了。希什提出了证明构形可约的那些著名的方法,并且指出,至少有一个方法(肯普所用的方法的直接推广)原则上是可以由计算机执行的充分机械的手续,希什的学生卡尔 · 杜尔(Karl Dürre)后来编了计算机程序,用这个手续来证明构形可约,只要这样一个程序成功地证明了一个构形可约,该构形就肯定是可约的了,可是,相反的结果只不过表示这个特殊的证明可约性的方法还不足以证明该构形可约而已;或许用别的方法还是可以证明它可约的。有时候,杜尔的程序未能证明一个构形可约,希什却成功了。他能够用这个程序所产生的数据以及用贝尔柯夫建立的更强的技巧进一步计算来证明该构形可约。
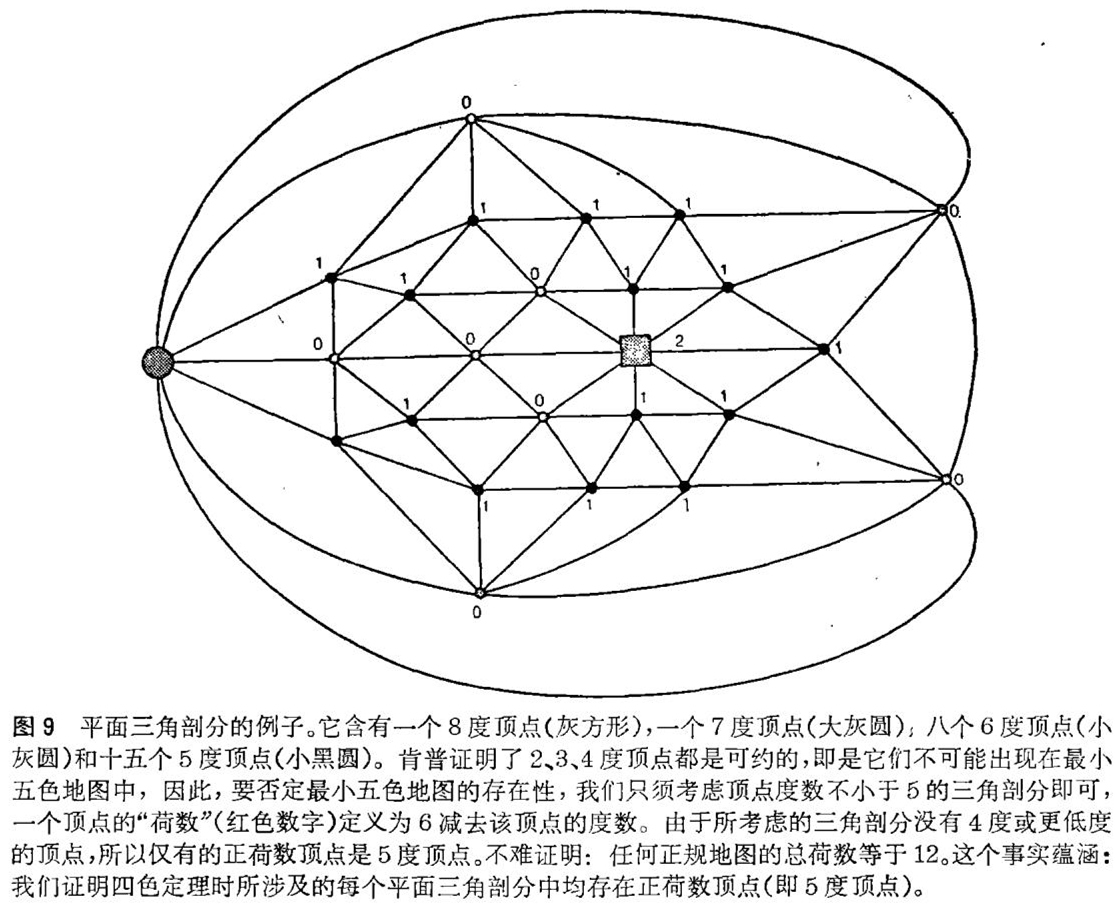
希什是用一种方便的方式来描写构形的,他首先把原来的地图变成数学家所谓的对偶形式——平面图(planar graph),其中图的每个顶点代表一个国家,而顶点间的每条线段则代表一条国界,为了得到一张地图的对偶图,标出地图上各国的首都,然后,只要两国相邻,就用一条道路穿过共同边界把它们的首都连结起来(见图8),现在在地图上把一切都抹掉,只是除了你所加的首都(称为顶点)和道路(称为棱)而外,这些顶点和棱就构成原地图的对偶图,一个图的棱把平面分成区域,称为面,如果原来的地图是正规的(证明四色定理时只需考虑正规地图),那么所有的面都是三角形,在这种情形下,对偶图称为三角剖分,在(对偶图中)一个特殊的顶点处会合的棱的数目称为该顶点的度数,等于(原地图中)那个顶点所代表的国家的邻国数。由棱组成的一条路径,如果在同一个顶点处出发并终止且不自身交叉,就把这个图分隔为两部分,它的内部和外部,这样一条路径称为回路。
用对偶图的语言来说,一个构形乃是一个三角剖分的一部分,由一组顶点再加上连结诸顶点的所有的棱组成。与这个构形相邻的那些顶点以及连结它们的棱组成的边缘回路,称为该构形的圈(对偶图中的圈相当于原地图中包围该构形的国家组成的圈)。构形经常用它的圈的长度来说明:例如,圈长为6的构形就是边缘回路正好有六个顶点的构形。
希什的工作出现以后,可约构形的理论似乎发展得非常好了。虽然在证明可约性的方法上后来做了某些改进,但是证明四色定理所必需的可约性思想,却是在二十世纪六十年代后期才全部得到理解,在找出构形的不可避免集方面没有取得可以比美的进展。希什引进一个找出构形(不必可约)的不可避免集的方法,类似于电网络中的移动电荷,但是他对待不可避免性思想却不是像他对待可约性思想那样热心。可是,最初以相当初等的形式在希什的工作中出现的这个“去荷”方法,在以后关于不可避免集的整个工作中却是有决定性意义的。它成为证明四色定理的中心要素,但形式复杂得多,所以我们稍微详细地来解释一下。
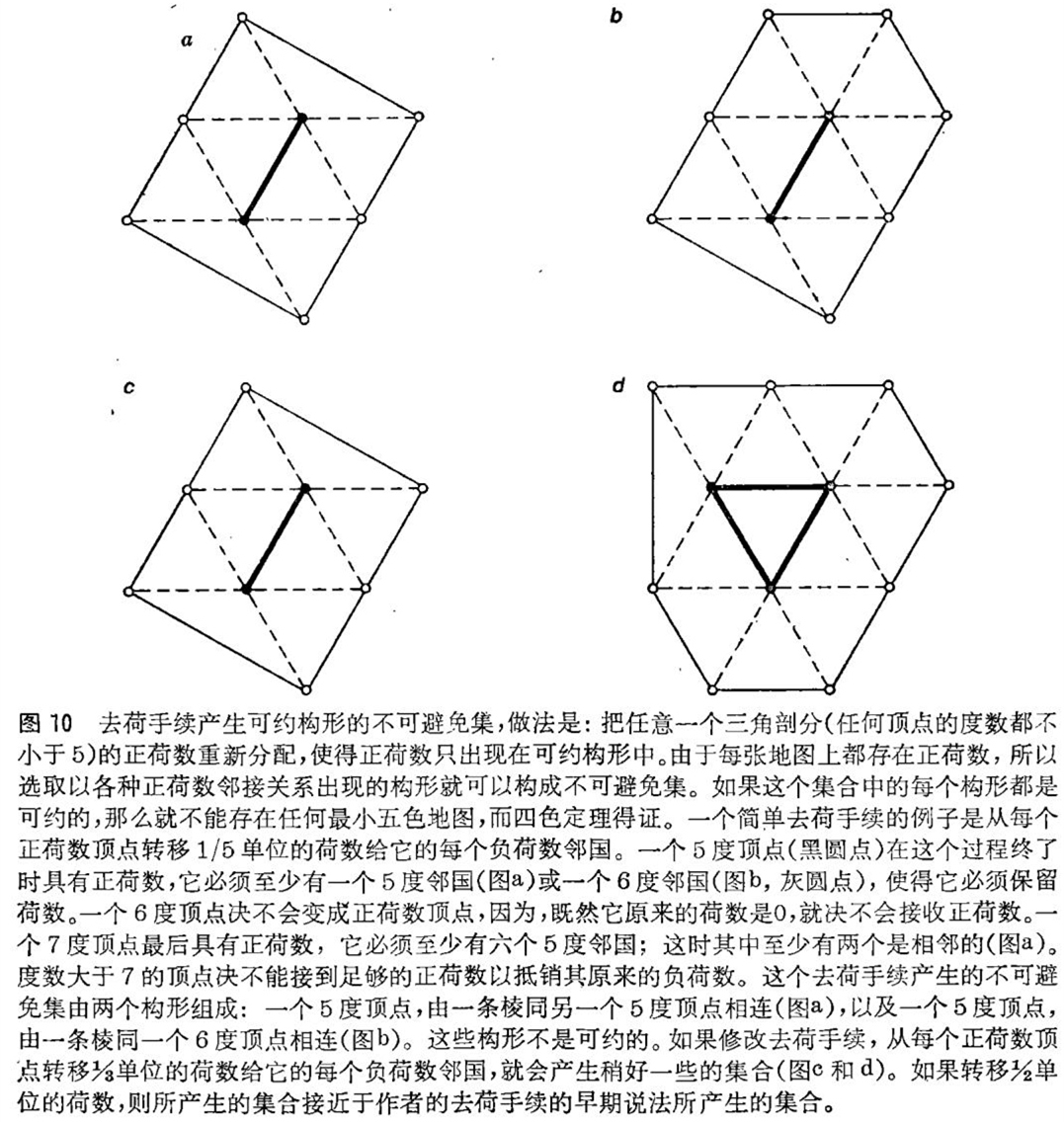
肯普的工作表明,代表一张最小五色地图的三角剖分不能有任何顶点其邻国少于五个。所以,下面为方便起见,我们用三角剖分这个词来表示任何顶点的度数都不小于五的三角剖分。如果对于每个k度顶点(即是有k个邻国),我们给他一个荷数6-k,那么度数大于6的顶点(称为主要顶点)就得到负的荷数,而只有5度顶点才有正的荷数。从肯普的工作可见,任何三角剖分的所有荷数之和正好是12。这个稍微令人吃惊的结果是因为对偶图是画在平面上¥且是一个三角剖分的缘故。12这个具体的和数并不很重要。非常重要的是:对于每个平面三角剖分而言,这个荷数和是正的(见图9)。
现在假设,这样一个三角剖分中的所有荷数被重新分配,但是搬来搬去并不丢掉或增加整个系统的荷数。特别是,假定正荷数从某些正荷(5度)顶点搬到某些负荷(主要)顶点。这些运算肯定不可能改变荷数的(正)和数,但是具有正荷数的顶点却可能改变;例如,某些5度顶点可能失掉正荷数(成为去荷顶点),而某些主要顶点却可能取得这样多的荷数,结果它们具有正荷数(成为超荷顶点)。不同的顶点按照所选的去荷手续或重新分配手续而成为去荷顶点或超荷顶点。
可是,对任意的对偶图给了详细说明的去荷手续之后,可以把经过去荷之后含有正荷数顶点的所有构形列成一张有限的表(当然,这些构形中每一个都可以重复不可预见的若干次)。换言之,正荷数只能出现在这个有限的构形集中。由于总荷数总是正的,所以总有某些顶点具有正荷数。因此,由于这张构形表中包含着所有可能的含有正荷数顶点的构形,所以每个平面三角剖分必须至少含有这些构形之一。这个过程(从任意一张地图产生特定构形的表)是可行的,因为可以确定该地图的小块分布情况而不必知道完整地图的形状。
在证明四色定理时,这种对正荷数顶点去荷的目的是要找出一手续,恰当地说明如何移动荷数,以保证在产生的构形中每个正荷数顶点要么属于一个可约构形,要么与之相邻。由于由这个手续标志出来的构形必定构成一个不可避免集,如果这些构形也是可约的,那么四色猜测就得到证明了。当然,如果产生的构形中并非全都可约,那么就没有取得任何真正的进展。事实上,肯普的不可避免集可以看成是完全不移动荷数这个不起作用的手续产生的不可避免集。
举一个相当简单的去荷手续以及相应的不可避免集的例子,可以澄清这些思想。考虑下述手续:从每个5度顶点转移1/5单位的荷数到它的每个主要邻国(见图10)。相应的不可避免集由两个构形组成:一个是一对5度顶点,由一条棱连结起来;另一个是一个5度顶点,由一条棱连结到一个6度顶点。
这些构形得到如下。一个5度顶点在这个手续终了时具有正荷数,它至少有一个邻国不是主要邻国,所以这个顶点必定保留正荷数;这个顶点或者有一个5度邻国(相应于不可避免集中第一个构形的情况),或者有一个6度邻国(第二个构形)。
—个6度顶点原来的荷数是0,因而不能接收任何荷数。一个7度顶点在手续终了时具有正荷数,它必须至少有六个邻国都是5度顶点;如果它至少有六个这样的邻国,其中必有两个由一条棱连结起来(不可避免集的第一个构形)。一个8度或更高度的顶点结果不可能具有正荷数,即使它所有的邻国都是5度顶点。检查一个8度顶点就可明白这个情况:它的原荷数是-2,而它能接收的最大正荷数是1/5的8倍,即1(3/5)。于是,这两个(不可约)构形构成一个不可避免集,即是,由于这些计算适用于任何平面三角剖分(任何顶点的度数不小于5),所以每个这样的平面三角剖分都含有这个不可避免集的两个构形之一。
1970年,作者之一(哈肯)曾经指出一些改进去荷手续的方法,开始希望这些改进可能会产生四色猜测的证明。可是,困难仍旧显得可怕。一个困难是:人们认为,可约构形的任何不可避免集中会含有很大的构形(邻国圈包含的顶点有18个之多)。这就意味着这个问题可能超出了现有计算机的能力,因为对于包围圈很小(可以多达11个顶点)的构形而言,在计算机上检查其可约性虽然是相当简单,但是,圈的长度每增加一单位,所需的计算机时间就增加四倍。更不妙的是,计算机存储量也要求增加得同样快。当杜尔的程序应用于一个特别困难的圈长14的构形时,花了26小时来证明该构形甚至不满足可约性的最机械的定义(用最少的机器指令叙述的定义)。即使检查一个圈长14的构形所需的平均时间不过是25分钟,但检查一个一般的圈长18的构形就会需要44×25分钟,即100小时以上的计算机时间,所需的存储量也超过任何现有计算机所允许的程度。
另一个主要困难是:没有一个人真正知道究竟需要多少可约构形才能构成一个不可避免集。看来,很可能构形的数目会成千上万,而且定不出一个上限。假定说,在一台有足够存储量的计算机上证明一个圈长18的构形可约要花100小时。如果不可避免集中有1000个圈长18的构形,那么在一台很大的计算机上证明这些构形可约就要花100,000小时即11年以上的时间。要是不可避免集真有那么大的话,我们的证明就只有等待计算机比目前通用的还快得多才能收到实效了。
即使四色定理可以通过找出可约构形的不可避免集而得到证明,但这种证明却不会使那些要求数学优美的人感到满意。使很多数学家更加恼火的是,没有一个人能够凭手检验不可避免集中所有构形的可约性。可是,到1970年,很多四色问题专家对于找到一个简短的证明却是相当悲观的。这个问题自从一百多年前提出以来一直受到密切的注意。对这个问题曾经试过许多办法,但是任何办法也没有产生四色定理的证明,虽然有些办法在其他数学领域中产生了重要的结果。
我们是1972年开始搞这个问题的,当时我们确信,我们所掌握的技巧不会产生一个非计算机证明。我们甚至非常怀疑,在强大得多的计算机造出之前,这些技巧会产生什么证明。因此,在我们进攻找出可约构形的不可避免集这个问题时,第一步就是要确定是否有希望找到这样一个集合,其构形的包围圈充分小,使得证明可约性所需的计算机时间会有适当的界限。按照这个问题的本性,显然,我们不应该首先考察所考虑的全部构形的可约性;否则进行估算所花的时间就会超过整个任务所需要的预计时间。
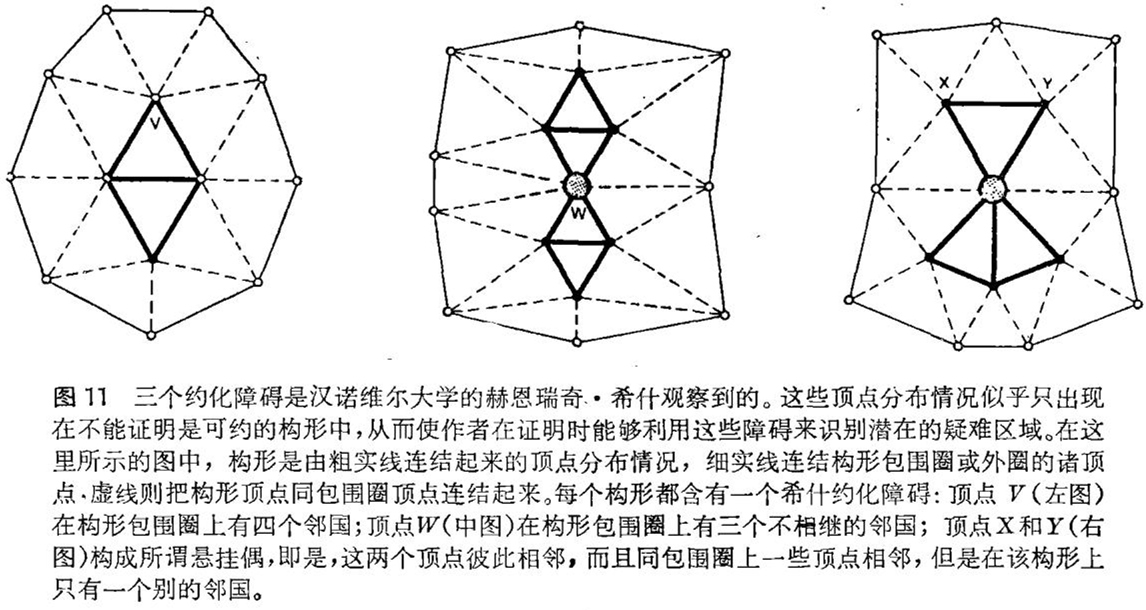
这里,希什有个思想是非常有用的。当他检查构形的可约性时,他注意到对约化成功的可能性提供线索的一些突出的现象。例如,存在某些条件,涉及构形顶点的邻国,在这些条件下,从未发现过构形是可约的。从未发现任何可约构形,比如说,至少含有两个顶点、含有一个与包围圈的四个顶点相邻的顶点并且不含任何更小的可约构形。虽然不知道如何证明具有这些约化障碍的构形不可能是可约的,但是看来采取下述假设才是慎重的:要想得到可约构形,就应该避开上述构形。希什发现三个主要的_化障碍,包括上面所说的那个;这些障碍是容易说明的(见图11)。含有这些障碍之一的任何构形都不曾被证明是可约的。
容易确定构形是否含有约化障碍;没有约化障碍的构形很可能是可约的。如果存在由没有约化障碍的构形组成的一个易于处理的不可避免集,我们觉得就一定会有一个不可避免集,大小大致相同,只含有可约构形。
因此,我们决定首先研究去荷手续的某些类型,以便确定可能出现的无障碍构形集合的类型。为了体会到究竟需要什么,即使对于这种研究,我们也把已经受到限制的问题再限于所谓的地理分布良好的构形:不包含希什三障碍中头两个障碍的构形。
1972年秋,我们编制了一个计算机程序,执行我们觉得最合理的那种特殊的去荷手续。我们并不准备证明四色定理,所以我们的程序的输出并非不可避免集,而是由最重要的情况产生的那些构形的表。虽然不可能指望计算机程序会像人一样聪明能干,但是计算机的巨大速度却能够容忍一定的无效性。不管怎样,程序的编制使得对它的输出可以容易地凭手检验。
1972年底,计算机程序的头一组试验使我们得到许多有价值的信息。首先,地理分布良好的构形如果大小适当(包围圈的长度不超过16),似乎会同具有最终正荷数的大多数顶点接近。其次,同一些构形出现得足够频繁,以致构形表似乎可以具有可控制的长度。第三,最初编制去荷手续时,计算机输出大得无法处理;相似的情况老是重演同样的论证。第四,去荷手续显然有些毛病,因为有些顶点具有最终正荷数,却不能保证它们的邻国中有地理分布良好的构形。最后,这个程序只用几小时就产生大量的信息,使得我们知道经常试验是可能的。
程序和去荷手续的某些方面必须加以修正,以克服头一组试验所指出的问题。由于我们可以保存基本的程序结构,所以修正是不难作出的。一个月以后我们进行第二组试验。既然主要问题已经纠正,所以我们能够发觉一些较难捉摸的问题。经过研究,我们找到了这些问题的解答,再次修改程序。
人机对话又继续了六个月,直到我们感到,到适当的时候,我们的手续就会得到地理分布良好的构形组成的不可避免集。到了这个地步,我们决定正式证明这个手续会给出地理分布良好的构形组成的有限不可避免集。我们不得不把实验方法放在一边,说明总的手续。必须证明全部情况都包括尽净,而未被计算机处理的那些情形却正是像它们看起来那样简单。
使我们非常惊讶的是,这个任务原来却是极端困难,花了一年多的时间:必须对一些术语提出一般的定义,证明涉及这些定义的一些抽象的论断;一些特殊情形,甚至实际上不大可能发生的情形,也必须详细考察,往往需要复杂的分析。最后,到1974年秋,我们得到一个冗长的证明:的确存在地理分布良好的构形组成的有限不可避免集,而且我们有一个手续来构造这样一个集合,其中构形的大小具有精确的界限,虽然比想要的界限大得多。我们设计的这个手续对我们是极端重要的,因为我们打算用它来证明四色定理(不久以后,瓦尔特 · 斯特隆魁斯特(Walter Stromquist)这位约化理论的主要贡献者,当时还是哈佛大学的研究生,对于地理分布良好的构形组成的不可避免集的存在性想出了一个优美的证明。不过,斯特隆魁斯特的证明并未提供实际构造这个集合中的构形的方法,所以看来这个证明不大可能会立即应用于四色猜测本身)。
当我们证明了我们的手续对地理分布良好的构形有效时,我们仍然不知道执行这个手续会有多么复杂。我们决定对于不含任何一对相邻的5度顶点的三角剖分这个受限制的问题来试试这个手续。当然,这是一个很强的限制,但是,我们所得到的地理分布良好的构形组成的不可避免集却相当小:只有47个构形,其中任何一个的包围圈的长度都不大于16。我们猜想,对于未加限制的问题的解可能会庞大50倍(结果这是乐观了一点),所以我们判定完全有理由继续下去。1975年初,我们修改程序,使得它产生没有障碍的构形而不是地理分布良好的构形;硬是用这个程序来寻找一些集合,使得较多的构形有小的包围圈。当我们试验修改后的程序时,某些缺点清楚了,而且还发现一个非常有意思的出乎意料的事实:把地理分布良好的构形换成没有障碍的构形仅仅把不可避免集加大一倍。
这个程序,我们两年来不断加以设想和改进,到了这个地步,使我们感到惊奇起来。当我们凭手检验早期的程序所产生的分析时,我们总是能够预言分析的进程,而现在计算机表现得像一台下棋的机器了。它根据已经学过的所有技巧制定复合的策略;新的方法往往比我们原来想试的方法聪明得多。在某种意义下,这个程序不仅在任务的机械部分而且在某些智力方面也表现出优越性。
到1975年夏天,我们相信,我们很有可能会找到一个不可避免集,其中每个构形都是没有障碍的而且很可能是可约的。这样一个集合一定会含有某些不可约构形,但是我们觉得,把手续稍加变化,我们就能够把它们换成可约构形。现在,我们第一次要检查构形的可约性了。
我们首先就最机械的可约性编制检查程序,用伊利诺斯大学(University of Illinois)IBM 360计算机的汇编程序语言进行工作。前年秋天,一位计算机科学的研究生约翰 · 柯奇参加了我们的工作,他想写一篇关于小包围圈构形可约性的学位论文[曼尼托巴大学(University of Manitoba)的佛兰克 · 阿奈(Frank Allaire)和罗德西亚大学(University of Rhodesia)的埃多德 · 斯瓦特(Edward Swart)当时正在做有点相似的工作,我们并不知道] 。截至1975年秋,柯奇已经对圈长直到11的构形中最机械的可约性问题编制了检查程序,并且继续搞了一些更一般的研究。在以后的几个月里,在柯奇的帮助下,我们修改了他关于圈长11的构形的工作,以编制圈长为12、13和14的构形的可约性的检查程序。最后,我们进一步修订这些程序,以便应用贝克柯夫建立起来的更一般的约化手续。
到此,我们关于去荷手续的工作走到了一个死胡同。为了改进程序需要有结构性的变化,而不仅仅是调整参数和某些琐碎的附加成分,而且每种变化都意味着对程序的重要修正。因此我们决定抛弃程序,凭手完成去荷手续。这会保证较大的机动性,使去荷手续可以在必要时加以局部的修正。1975年12月,我们得到一个令人鼓舞的发现:定义我们的去荷手续的规则中有一条太苛刻了,放松这条规则则使去荷手续更加有效。
有了新的去荷手续,看起来好像我们能够建立一个不可避免集,其可约构形会比早期的手续所产生的构形小些;证明四色定理所需要的计算机时间大概会比原先的估计少些。不过,为了得到可约构形组成的最佳不可避免集,需要相当大的计算上的劳动,这一点还是很明显的。威斯康辛大学(University of Wisconsin)的埃多德 · 佛 · 穆尔(Edward F. Moore)建立了一个强有力的方法,以构造不含小的可约构形的地图。例如,他创作了一幅地图,其中最小可约构形的圈长是12。因此,可约构形组成的任何不可避免集必须至少有一个圈长12的构形。穆尔的工作提供了圈长的一个下界,但是我们现在确信,圈长13是必要的;很可能,圈长14也是必要的(我们的证明表明不需要更大的构形)。
1976年1月,我们开始用我们新的去荷手续构造可约构形的不可避免集。去荷手续的这个最后方案还有一个优点,就是保证最终构形的可约性。这个手续本质上是自身修正的;设计出的程序能够识别出关键区域,或疑难区域(即是看起来好像拒绝接受约化的一些构形),并能自我修正,把正荷数搬到不同的地方。由于我们是不用计算机进行去荷手续,所以我们知道,当我们碰到关键区域时,去荷手续是能够得到修正的。
我们首先作近似安排,即是对我们的去荷手续进行初步试算。我们考虑一定有一个顶点具有正荷数的各种可能的情形;在每种情况下检查其邻域以找出一个没有障碍的构形。如果一无所获,这个邻域称为临界的,这就意味着必须修正去荷手续以避开这个问题。可是,即便找到一个没有障碍的构形,我们也不能保证有一个可约构形。新的约化程序用来尝试在该邻域中找出某个没有障碍而且也是可约的构形。如果一无所获,这个邻域也称为临界的。
这种(改进去荷手续)推演可约构形的不可避免集的方法,只有靠另一次人机对话才行。为了确定哪些邻域是临界的,不论就计算机时间或实际时间而言,都必须快速检验可约性。幸好,几乎不需要花好几天来等待结果,尽管往往需要相当多的计算机时间。由于这种深入的人机相互作用是我们的工作所不可缺少的,所以我们应该说明一下其所以能够实现的情况。
我们准备使用计算机,虽然在当时对我们是很自然的,可是我们后来发现,我们真是运气好,是在伊利诺斯大学工作,那里巨大的计算机构的联合以及对待把计算机用于研究目的的开明方针,使我们得到似乎在几乎任何其他大学或研究机构都不可取得的机会。虽然我们不能保证我们的工作会产生四色定理的证明,但是却优厚地给我安排了1000小时以上的计算机时间,我们感到,这令人钦佩地显示出对纯数学研究的价值的信念。计算机中心通知我们说,因为大学的计算机在教学任务以及其他各种研究上老是得不到充分的利用,所以我们可以加入一个计算机使用人员的小组,分享剩余的计算机时间。我们现在知道,这个方针对我们的工作是必不可少的。
1976年6月,我们完成了构造可约构形的不可避免集的工作;四色定理得到证明。我们在三台不同的计算机上用了1200小时的时间。最后的去荷手续与我们最初的近似安排相比,大约差了500次由于发现临界邻域而产生的修正。推演这个去荷手续需要凭手分析大约10,000个正荷数顶点的邻域以及机器分析2000多个构形。最后的证明中利用了这项资料的相当大一部分,包括约化1482个构形在内。虽然去荷手续(不考虑约化)可以在几个月内凭手检验,但是凭手验证约化计算实际上是不可能的。事实上,当我们把我们的文章校样提交伊利诺斯数学杂志(Illinois Journal of Mathematies)时,审稿人检验了我们定稿中的去荷手续,但却使用一个独立的计算机程序来检验可约性计算。
很多数学家,尤其是高速计算机发展起来以前受教育的数学家,反对把计算机当作一种标准的数学工具。他们觉得,一个论证的全部或一部分不能通过手算而得到核对时,这个论证就站不住脚。从这个观点看来,由独立的计算机程序来验证我们这样的结果,并不是像用手核对证明那样令人信服。数学定理的传统证明是相当简短而且高度理论性的——理论越有力,证明越优美;所以用手核对证明通常是最好的方法。但是,如果证明很长而且计算复杂,那么,用手核对即便可能,也很难相信就一定会找出所有可能的错误。此外,如果计算是像我们的证明里那样一种充分机械的手续,那么用机器程序核对大概也比手算核对更有效些。
如果说,很多数学家对冗长的证明感到厌烦的话,那也许是因为直到最近他们还只是使用形形色色的产生简短证明的方法的缘故。我们还不知道,是否能够找到四色定理的简短证明;过去曾经宣布过好几个长度适当的新证明,但是其中没有一个经得起专家的细致推敲。虽然可以设想总有一天会找到一个有效的简短证明,但是也可以想见,唯一正确的证明将基于可约构形的不可避免集,因而需要只用手是完成不了的一些计算。我们认为,有一些具有重大数学意义的定理只能用计算机方法来证明。即便四色定理不是这样的问题,它也提供出一个好的榜样,说明可以怎样来证明一个定理。没有理由认为,不存在大量的问题需要这种不同类型的分析。
我们对四色定理的证明说明在数学上单凭理论方法所能取得的成就是有限度的;它也表明,过去,低估了数学证明中对于计算方法的需要。对数学家说来,确定他们的方法的威力和限度是有巨大实际意义的。我们希望,我们的工作将加速这个方向上的进展。扩大了可以接受的证明技巧这一概念,说明过去一百年来对于证明四色定理所献出的巨大劳动没有白白浪费。
[译自Scientific American1977年237卷10期。江嘉禾译]
—————————
① 美国大学通常由几个独立的学院组成,这里是指伦敦大学的一个学院。——译者注