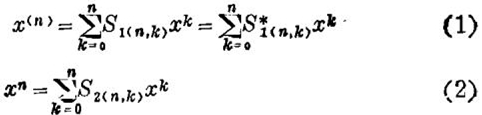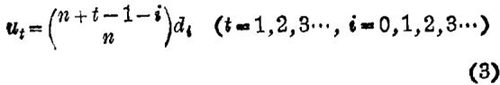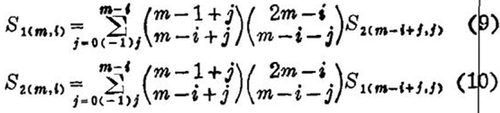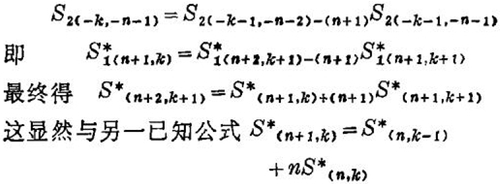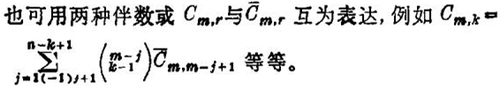中算传统方法与两种计数函数

发布时间：88年09月25日

傅庭芳

中国的传统数学与西方数学代表着两种不同的体系，思想与方法。我国的传统数学着重于机械化的思想方法与算法形式，西方则着重以定理表达的概念与演绎。宋元以后我国数学停滞不前，逐渐丧失了领先世界的地位。西算传入后，我国的数学传统长期被人忽视，即使有很好的方法与成果，也几乎湮没无闻。近来由于计算机科学蓬勃发展，我国注重算式和机械化的思：想方法因合乎现代要求开始被人们所注意。事实上，我国的传统数学中确有许多独特的思想和方法，如“形数结合”、“比类”等，以经典问题的解为样板，比较同类事物来解决新的问题，处理新的情况，与西方不同，可用较简捷的直观方法取得至今未被外国发现的成果，如清末李善兰的“垛积差分”方法，与“李善兰多项式”是很好的成例。此外，由于计算机科学和许多科学领域发展的需要，发源于我国的组合数学也蓬勃兴起，而应用中国传统的数学方法来研究组合数学中的一些问题也简便实用且具有新意。以下介绍用“垛积差分”“比类”与“形数结合”的中算传统方法阐述与组合数学中两种有名的计数函数——司脱林数（Stirling numbers）和卡他兰数（Catalan numbers）有关的几个方面。

—、垛积差分与两类司脱林数

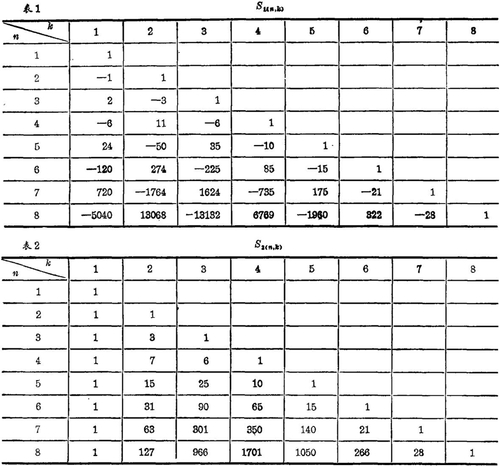
如所周知，阶乘函数x⁽ⁿ⁾(=x(x－1)…(x－n+1))与幂函数xⁿ(n=1，2，3…)前者在组合分析与有限差分中，后者在数学分析中，具有同样的重要性，而司脱林数恰好是这两套基底函数的变换系数，并经常出现于许多具体计算之中。据所见已发表的各种中外著作，都只能用一种数表、算法或组合关系来处理第一类司脱林数，用另一种来联系第二类司脱林数。而用垛积差分及比类则可用一种数——数S_m,l来统驭这两类数。就绝对值而言，两类司脱林数可以合一，互相归并为一种函数。

两类司脱林数的定义如下：（以下用S_1(n,k)表第一类司脱林数S_2(n,k)表第二类司脱林数，S^*_1(n,k)表第一类司脱林数的绝对值。）

x⁽⁰⁾ =x⁰=S₁(0,0)= S₂(0,0)

具体数值如表1和表2

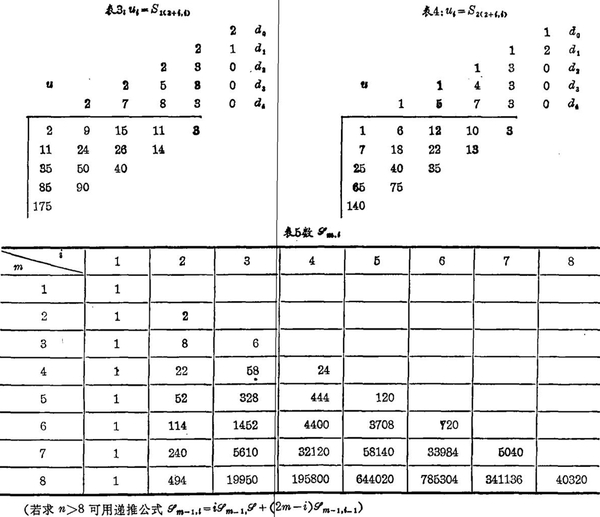
用表1、表2、的斜行各数S_1(m+i,i)，S_2(m+i,i)，（m，i=1，2，3，…）作序列（若m=2则序列是S_1(3,1)，S_2(4,2)，S_2(5,3)…等等，余仿此）可以看出由两类司脱林数所得的垛积差分系数是相反对称的，若m=2，取得垛积差分系数的垛积差分表如表3，表4。

把编号为m的第二类司脱林数的d₀，d₁，…d_m_－1，改写为Φ_m,1，Φ_m,2，…Φ_m,m便得表5。

按垛积差分原理，n次函数可取得n+1个垛积差分系数d₀，d₁，…d_n，该函数可表为

（关于垛积差分的简介。参见《自然科学史研究》1985年第3期。）

因司脱林数S_m+i,i是2m次函数，且d_m=d_m+1=…=d_2m=0，用m表m+i，即得求二类司脱林数的公式：

（7）与（8）是一个很有用的独创公式，这比以研究司脱林数闻名的Ch. Jordan的《有限差分学》所引的两种司脱林数的转换公式

要简便得多。

用公式（7），（8）只要把两类司脱林数中的一个互换前后标加上负号，即可把已有的公式显示出新的关系，得出新的公式，把已知的公式几乎可以扩充一倍。比如说把前后标互换则（5）式变为（6）式，反过来也一样。用垛积差分来处理幂函数，能显出极大的对称性，对称性之一是：倘两个2m次函数的垛积差分系数有d_m=d_m+1=…=d_2m=0，它们间的d₀至d_m-1互反（如表3的2，1，与表4的1，2），则其中一个序列依次乘以1，2，3，…，另一个依次乘以m+1，m+2，m+3，…，所取得的新的垛积差分系数仍是反相对称，且两个序列可归并为一个，即一个序列是u₁，u₂，u₃…，而另一个序列为它的u_-m-1，u_-m-2，u_-m-3…。两类司脱林数的绝对值恰恰具备这种性质，这可直观地用表6和表7的差分表来说明。

我们也可以用两类司脱林数的基本（递推）公式，用（7），（8）两式转换来说明其同一性。比如原递推公式有S_2(n+1,k)= S_2(n,k-1)+kS_2(n,k)经转换后有：

及S_1(n+1,k)= S_1(n,k-1)－nS_1(n,k)等价的。用S₁的基本公式经同样处理，也可得到S₂的基本公式。

因为两类司脱林数可以合而为1，在著作如Ch. Jordan的《有限差分学》，J. Riordan的《组合分析导论》等著作中用数C_m,r，Cˉ_m,r和司脱林伴数（Associated Stirlingnumbers of the first（second）kind）来表两类司脱林数，用公式（7），（8）的关系，能使本来用一种数表来表达一种司脱林数的用来表达另一类司脱林数，

二、形数结合与比类引出的卡他兰数三角阵

卡他兰数（Catalan numbers）是组合数学和图论中的重要计数函数，其递归关系是非线性的，有多种用途。

用途如：

1. n个文字x₁，x₂，…x_n，把这些文字依其足标的顺序作底的各层幂，所得n重幂的个数为C_n-1个。

2. 一个凸n边形通过不相交于n边形内部的对角线，可拆分成C_n-2个三角形。

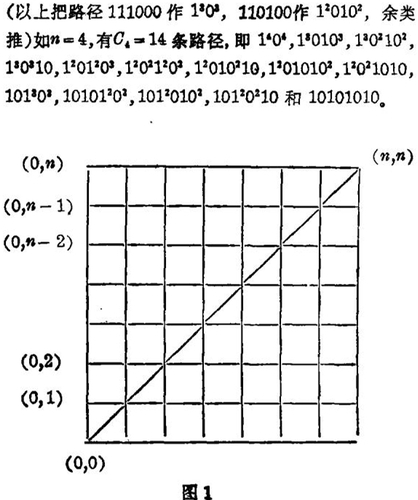
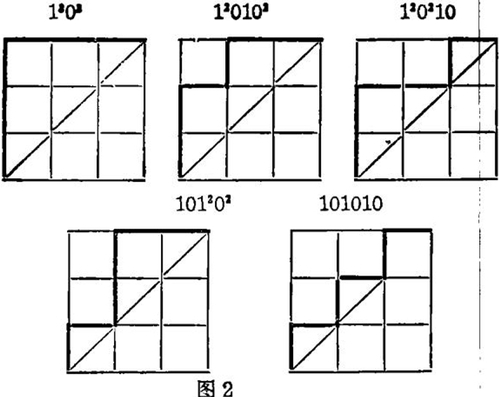
3. n个1与n个Q组成一个2n位的2进制数要求从左至右扫描，其中1的累计数不小于0的累计数，满足此条件的数有C_n个。此问题相当于有n×n格的正方形图，以左下为原点（0，0），右上为（n，n），从（00）出发向上移一格作一，向右移一格作0，但不能后退或超过对角线，从（0，0）到（n，n）如图1的路径数有C_n条，例如n=3时有路径5条如图2粗线所示：

关于卡他兰数是如何组成的，有几种方法？在组合数学的著作上未见介绍。现知有两种方法。

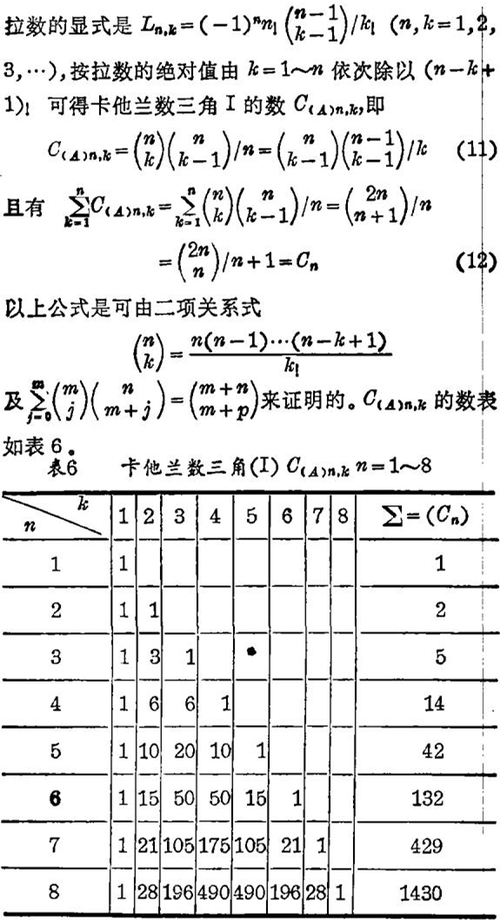
用我国传统的比类方法对与司脱林数有密切关系的一种数拉数（Lahnumbers）进行比较观察，我们发现

C_(A)n,k有对称性C_(A)n,k=C_(A)n,n-k+1。从垛积差分角度来看也有特殊性质，序列C_(A)n,n， C_(A)n+1,n，C_(A)n+1,n，C_(A)n+2,n，这一列的垛积差分系数就是C_(A)n-1,1，C_(A)n-1,2，…C_(A)n-1,n。例如表6中k=4的序列1，10，50，175，490…那一列，其垛积差分系数就是1，3，1。

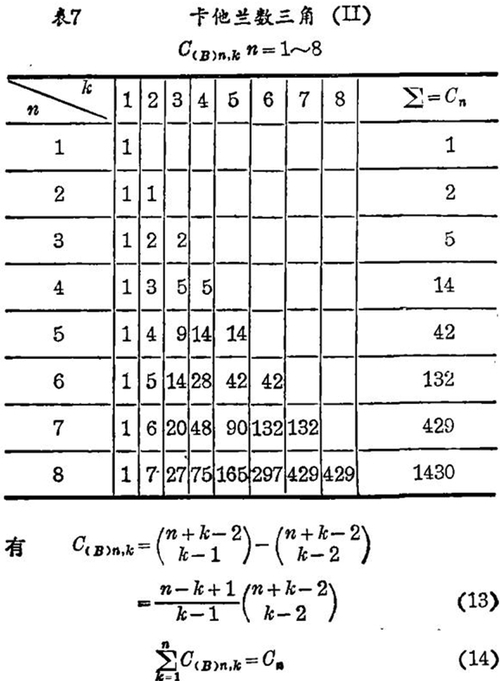
另一种组成是卡他兰数三角（Ⅱ）——数C_(B)n,k，可从n个文字的n重幂的递归关系引出，也可联系到勒让德多项式（区间（0，1））。数值如表7：

卡他兰三角数C_(A)n,k和C_(B)n,k的组合意义是什么，有无相通之处？我们可用卡他兰数三角阵来解决这个问题。

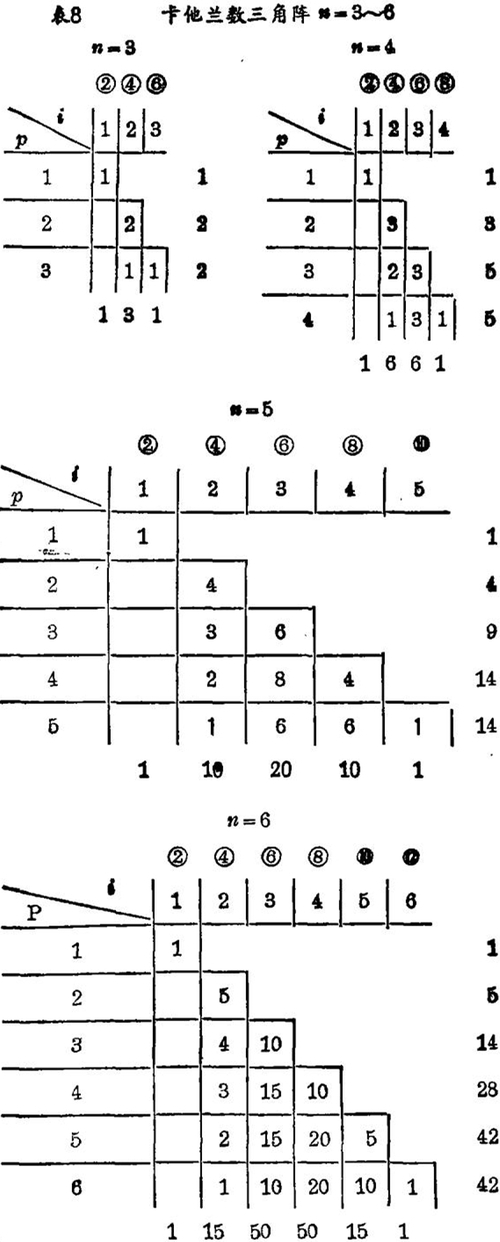
看图2，从（0，0）开始向上移动1^m次后，要遇到0才有一个转折，从0^m向右要遇到1才有转折，故只要去掉1或0上面的指数记号计算共有多少个1和0便知有2，4，6以至2n个转折各有几个。图2即n=3的情况，有2折途径1个（1³0³），4折途径3个（1²010²，1²0²10，101²0²）和6（=2n）折途径1个（101010），就是C_(A)3,k所示的途径。从另一方面看，从1³，1³，1开始转折的途径各有1，2，2条就是C_(B)n,k所示的途径。若n=4，则具有2，4，6，8（=2n）个转折的路径的分别有1，6，6，1条，从1⁴，1³，1²，1开始转折的各有1，3，5，5条，就是C_(A)4,k和C_(B)4,k所示的路径。再归纳由1ⁿ，1^n-1，…1开始转折的2，4，6，…，2ⁿ个转折的路径各有几条，就得卡他兰数三角阵，n=3 ~ 6的三角阵如图3。