无穷大始终是一个不可靠的概念。即使是由乔治 · 康托尔提出的为人们普遍接受的数学观念,也没有真正把无穷大置于严密的基础之上。
2000多年来,数学家扣大部分人一样,不知道拿什么去解释无穷大。希腊和中世纪的思想家所作的几个悖论使数学家们相信,无穷大是经不起推敲的。到了18世纪80年代,德国数学家乔治 · 康托尔揭开了超穷数学(一个数学分枝)的书页,好像解决了无穷大提出的全部问题。康托尔在著作中证明:无穷大数是存在的,它们以不同大小的规模出现,并且可用来度量各无穷集合的广延。然而他真的把无穷大在数学处理上的所有疑问都消除了吗?大多数人认为他消除了,可是我要在本文中提出,事实上他使这种疑问加深了。
数学家向无穷大开战起始于公元前5世纪。那时巴门尼德(古希腊哲学家,爱利亚学派创始人——译者)的一个学生芝诺系统地提出著名的“埃几尔斯(半神)和乌龟”悖论。这个难题是说,奔跑快捷的半神(他)和爬行迟缓的乌龟(她)赛跑,他让她把起跑点定在他的前头。在他能超越她之前,必须先跑到她的起跑点。但这时她已经往前跑了一段距离。现在半神必须再跑完他们之间的新距离。但是在他补上这段距离之后,她又已前进了。照此进行,直到无穷。好像埃几尔斯永远赶不上乌龟了。曾纳同样论证:跑完跑道是不可能的。要跑完跑道就必须到达中途点,然后到达四分之三点,然后又到达八分之七点,以下依此类推。曾纳的结论是:不但这种运动是不可能的,而且我们最好不要用无穷大来思考问题。
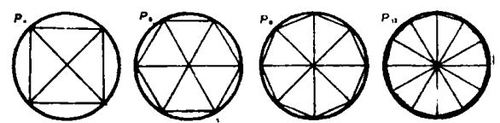
同样对无穷大抱提防态度的数学家欧道克修斯创立了所谓“穷举法”,在特定的几何学推导过程中他寘避了无穷大。大约100年以后,阿基米德用这个方法来求圆的精确面积。他是怎样进行的呢?他的部分过程是研究内接于圆C的n等边多边形的面积(称作Pn)公式。我在下图中说明的不是他的论证过程,而是对他的论证过程进行曲解,以使这个公式这用于圆本身——这个圆正好是无穷多个无穷小边的多边形。
如图1,设圆半径为r,对于每一大于2的整数n,我们可以构造一个规则多边形——内接于圆的n边多边形。这个n边多边形(Pn)可以分成n个等边三角形。bn为每一三角形的底,hn为高,则各三角形的面积为1/2 bnhn。因此,整个面积就是n(1/2 bnhn)或1/2 nbnkn。但c是一有无穷多的无穷小边多边形。换言之,当我们推广Pn的原来定义,让n为无穷大时,就产生c。这时,nbn是c的圆周,等于2πr(据π定义);hn是圆的半径,所以圆面积是1/2(2πr),即πr2。
对阿基米德的曲解具有一定的直观诱惑力,但是它并不满足阿基米德。我们不能不加鉴别地应用无穷大,彷佛它真的是某种不寻常的巨大整数。这里提到的部分是,n越大,Pn越接近于与c一致。但如下的说法也是对的:n越大,Pn越接近于有一处不平的圆,把它写作c*。很直观,关键在于c和它的变形了的对应物c*不同,c是诸多边形的极限,或者说,诸多边形趋向于圆。
还有,要不是把c看作是一个“无穷多边形”,就很难找到还有什么捕捉到这种直观性的办法。阿基米德提供了一个办法,他用证明下面这一点来准确确定c和c'的关键性区别:无论你认为面积ε是多么小,总存在一个足够大的整数n使面积Pn在c的区域里的ε之内。对于在c'的区域里,这种说法就不正确。这一事实,结合外接多边形的结果,并用他论证中所包含的精密逻辑作补充,使阿基米德能够不求助于无穷大而最后证明圆面积等于πr2。
现实的和潜在的无穷大
虽然阿基米德在这个特例中成功地回避了无穷大,但是毕达哥拉斯人(毕达哥拉斯建立的一个宗教团体)碰到了一种实在逃避不了无穷大的情况。这个发现打碎了他们对两个宇宙根本原则的信仰:Peras(有限)所客者皆好,Apeiron(无限或无穷大)所属者皆糟。他d本来坚决主张,宇宙万物可以用正整数来理解,并且最终确实由正整数所组成,而每一个正整数都是有限的。他们认为,这种简约之所以可能,是因为这样的事实:Peras总是征服Apeiron。
然而毕达哥拉斯已经发现,直角三龟形的斜边平方等于另两边的平方和。给出这个定理,正方形对角线与任一边的比是√2 :1,因为12+12=(√2)2。如果Peras无动于衷,则这个比应当可用两个正整数p比q的形式来表达。可这是不可能的。设想两个正整数P和q,使P比q或P被q除的值等于√2。我们可以假设P和q没有大于1的公因子。(如果必要,我们可以用公因子来除,)P2是q2的两倍,所以P2是偶数。这就是说,P本身是偶数。因此,q必定是奇数,否则2就是它们的公因子。然而考虑一下:如果P是偶数,则必有一正整数r恰好是p的一半。因此,(2r)2等于2q2,或2r2等于q2。这就是说q2是偶数,随之q本身也是偶数。这同上面所证明的相矛盾。
这一结果对毕达哥拉斯人简直是灾难(传说他们中有人由于把这个发现泄露给敌人而遭海难)。他们已经找到一个“无理的”数。这么做之后,他们看到了正整数的缺陷,他们不得不承认在它们中间出现了无穷大。的确,现代数学家会说,√2是一种“无穷客体”,不但它的小数部分无穷扩展,而且这种扩展永远不取有限循环的形式。
公元前4世纪,亚里斯多德认识到一个更为一般的问题。一方面,我们被迫承认无穷大。不只是有关我们不得不说的那些,更有:时间显得无穷延续,数字似乎没有终点,空间、时间和物质好像是永远可分的。另一方面,我们在来自各方面包括芝诺悖论的逼迫下要抛弃无穷大。
亚里斯多德对这个两难问题的解决是巧妙的。他区分两种不同的无穷大。现实的(actual)无穷大,其无穷量存在于时间的某个点上;而潜在的(potential)无穷大,其无穷量散布在整个时间之中。亚里斯多德认为,所有对于无穷大的反对,都是反对现实的无穷大。另一方面,潜在的无穷大是真实性的基本特征。它在永远不能终结的过程中应该得到认可,这些过程包括计数,物质的分割以及时间通道本身。两类无穷大的区分提供了对芝诺悖论的解。通过一个空间区域并不就是运动通过子区域的现实无穷大,子区域的现实无穷大是不可能的。但是在划分空间的过程不能有终结这个意义上,它指的是通过子区域的潜在无穷大。幸好,这个结论是无害的。
亚里斯多德关于现实无穷大的和潜在无穷大区分被视为正统而长期保持有效。不过,学者们通常以时间为参照把它作为一种更深层的譬喻。现行的“准时”和现行的“同时”采取了广阔得多的含义。对现实无穷大的反对就是反对这样的观念:某种实体可以具有超越一切有限度量的性质;它还拒绝承认无穷大本身是正规的研究对象。
大约2000年之后,数学家在创立微分学中又一次受到无穷大(包括现实的和潜在的)的训练。由牛顿和莱布尼兹在17世纪引入的微分学,其早期工作远远够不上希腊标准的严密。的确,数学家已经无鉴别地推广应用无穷小——小得无法测量的量。有时这些量被看作等于零。例如,把它们加到别的数上,原来的数值保持不变。在另外一些时候,它们又取不等于零的数值,被用于除法。G · E · 安东尼写道:“一曲线可以看作无数直线段的总和,每一直线段无穷小;或者看作无数边的多边形到19世纪,法国数学家A · L · 柯西和德国数学家K · 威斯德拉斯才恢复了“穷举法”,给予微分学以坚实的基础。
无穷大和等多
柯西和维尔斯德拉斯的工作成果使大部分数学家不大害怕芝诺悖论了。那时,产生了一系列更重要的涉及等多性的悖论。这些难题是由下述原理推导出来的:若一集合的所有元可以与另一集合的所有元成对分置,则两集合必有相等多个元。例如,在一个一夫一妻制的社会中,丈夫数和妻子数一定一样多。这个原理看起来是无懈可击的。然而把它应用到无穷集合,似乎忽略了由阿几里德首先明确表述的一个基本概念:整体恒大于部分。例如,可以把全部正整数与那些偶数成对分置:1与2,2与4,3与6,如此等等。这里忽视了一个事实,正整数还包含着奇数。中世纪有许多类似的例子,有些是几何学上的。13世纪苏格兰数学家J · D · 斯高德斯对两个同心圆的事例疑惑不解:小圆的较短圆周上的所有点能够与大圆的较长圆周上的所有点成对分置。相应的结果适用于两个球,大约350年以后,伽里略讨论了偶整数成对事例上的变化,这里代之以整数平方。尤其令人吃惊的是,设想有越来越大的正整数序列的较大段,这些整数与其平方的比值趋向于零。然而成对过程还是无限地继续下去。
由于有这些困难,自然总是想整个避开无穷集合。更一般地说,总是想象亚里斯多德那样,不承认无穷多的事物能够同时聚集到一起。然而康托尔终于向亚里斯多德提出挑战。在他极为卓越的工作中,轻松地解决了悖论,表述了协调、系统和精密的现实无穷大理论,随时准备回答来自任何方面的怀疑。康托尔接受“成对分置”原理及其逆命题:两个集合不等多,除非它们的元可以成对分置。据此,他承认:偶正整数正好与正整数的总数一样多。
为了便于论证,也为了适应这一问题的现代数学惯例,就照此办理吧。如果这一原理是指的全部不大于它的各个部分,也照办不误。事实上我们可以应用这个观念去定义无穷大,至少在把它应用于集合时可以这样做:一集合是无穷集合,只要它不大于它的一个部分。精确一点说:一集合是无穷集合,只要它的元与它的一个适当子集的元一样多。
一旦事情以这样的方式阐明,留下值得怀疑的问题是,是不是所有的无穷集合都是等多的。康托尔著作中大量有影响的证明都不是这样的。有不同的无穷大规模,这个命题出自康托尔定理:没有什么集合,特别是没有什么无穷集合,它所有的元像它所有的子集一样多。换句话说,没有什么集合像它的子集一样大。为什么?因为如果一个集合是这样,它的所有的元就要能与它的所有子集成对分置。那么有些元就会与包含着它们的子集成对分置。另外一些则不会。这样,没有包含在已成对分置的集合中的元的集合会是怎样的情况呢?没有什么元可以无矛盾地与这种子集成对分置。
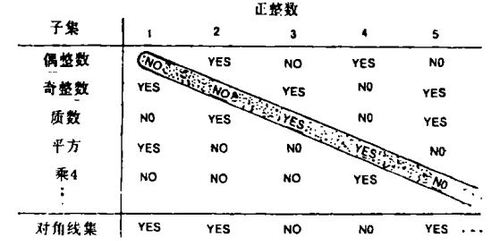
这一论证可以改写成图解(如下图)。为了方便,我们将集中注意于正整数集合。我可以用yes和no的无穷序列表示任何正整数集合的子集,按次登记下各正整数是否属于这个集合。例如,偶整数集合可以用下列序列表示:(no,yes,no,yes,no,……)相应于1,2,3,4,5等等。同样,我们可以表示奇整数集合:(yes,no,yes,no,yes……);质数集合:(no,yes,no,yes,no,yes……);平方集合:(yes,no,no,yes,no……)一般地说,对任何各别正整数的不同于子集的任何一种分配(诸如已作说明的纯粹任意性事例)都可以用yes和no的无穷方格来表示它。
为了说明至少有一个子集不在这个子集表里,我们作了一个新的子集。办法是把图中的“方格对角线”往下移动,每个yes用no去替换,反之亦然。把它们写作(yes,yes,no,no,……)。其结果即表示上述的子集,根据构造,这个子集就1是否属于它而与第一个子集相区别,就3是否属于它而与第三个子集相区别,就3是否属于它而与第三个子集相区别,如此等等。这是一个有趣的历史嘲弄 :正如当年对角线的研究使毕达哥拉斯人承认无穷(数)超出了对正整数的理解,坎托的遭遇亦复如此,只是方式不同罢了。
后来康托尔设计出无穷基数——能够用来测量无穷集合规模大小的数。他还为它们发明了一种计算方法。在定义术语之后,他探索了当一个无穷基数加上另一个时,当一个基数乘以另一个时,当它自乘时等等,会碰到什么情况。他的工作显示了最高质量的数学技巧。但是即便在他自己的术语中,困难依然存在。连续集问题恐怕是其中最出名的麻烦。我们知道,正整数集合比正整数诸集合的集合小。但小多少?尤其是,还有大小居中的集合吗?
康托尔的连续集假设
康托尔著名的“连续集假设”就是:无。但是他从来没有成功地证明这个概念,也没有推翻它。后来的工作说明,情况比他曾经想象得要严重得多。应用现代数学所承认的方法,问题都不能得到解决,这一难题引起了关于康托尔概念的确切性的哲学问题。要问连续集假设是否正确有点像问哈姆雷特是不是左撇子一样玄乎。看来对它的了解还不足以形成答案。如果这样,我们就应重新考虑,康托尔的工作是否足以制服现实的无穷大。
更为重要的是围绕所有集合的集合问题。已知康托尔定理,这一集合必然小于诸集合的诸集合的集合。然而且慢!诸集合的诸集合本身就是诸集合。因此诸集合的集合必然小于它自己的适当子集合,那是不可能的。整体可以与部分大小相同,但它不能比部分还要小。康托儿怎样逃脱这个陷阱呢?他异常固执,不承认有任何像诸集合的集合那样的东西存在。他的理由在于如下的诸集合图景 :有些东西不是诸集合,然后有所有这些东西的诸集合,然后有所有那些东西的诸集合。如此等等,没、有终结。每一集合属于某个更远的集合。但是永远不会出现一个每个集合都属于它的集合,康托尔的推理有点像是专为这一目的而设置的。但是像B · 罗素的著名悖论(1901年发现)那一类论证是必要的,这个悖论涉及一切集合的不属于它们自己的集合。称之为集合R。例如,老鼠的集合是集合的一个元,它之所以不属于它自己,是因为它是一个集合而不是一只老鼠,罗素悖论的关键在于R是否能属于它自己。如果它能,根据定义,它就不属于R。如果它不能,它就满足作为R的元的条件,从而属于它。从诸集合的各方面看,R总有些不可靠的东西。按照康托尔的看法,没有什么集合属于它自己,R(如果它存在)就是所有集合的集合。这一论证使得坎托图景以及与之相伴的对R的排斥,显得更为合理。
但是这个图景不是惊人的亚里斯多德哲学吗?不妨注意一下世俗的说法,集合被描绘成是出现在它们的元“之后”。按照这种说法,总还会有更多的元出现。它们的集团无穷量(作为与其中任何一个无穷量相对比)是潜在的,不是现实的。进而言之,难道不是这种集团无穷量最配这个资格吗?人们通常把无穷大定义为无终点的、无界限的、不可观测的、不可度量的。没有人会允许用一个无穷集合的学术定义来表达他对概念的直观理解。但是已知的坎托图景,无终性、无限性、不可观测性和不可度量性对整个体系比对其中的任一特殊集合更加合适。
然后,举例说,康托尔想了一些办法去证明正整数集合是“真正的”(really)有限的,而什么是“真正的”无穷大则不是这些办法所能证明的。(他本人不是不愿意用这些措词谈论问题)具有讽刺意味的是,他的工作好像使亚里斯多德正统有了具体内容:“真正的”无穷大可以是绝对不真实的。
有些学者反对我提出的:在康托尔概念中正整数集合是“真正的”有限的。他们分辩道,这种断言不但与标准的数学术语相抵触,而且似乎与我提到的相反,也与大部分人所说的相抵触。
是的,大部分人当然会说:正整数集合是“真正的”无穷大的。但是还有,大部分人不知道坎托的结果,他们也不知道一个无穷集合可以大于另一个无穷集合。我的论点不是关于大部分人怎么说,而是关于他们如何理解他们所用的名词,以及那样理解怎么能够为了任何既定目的而最好地吸收来自坎托结果的冲击。这里没有什么强制我们。我们可以说,有些无穷集合大于另一些。我们也可以说,正整数集合只是有限的。我们可以从一种说法改口为另一种,也可以不承认正整数集合的存在。
如果目前的工作是明确表达某种标准数学结果,我不主张应用标准数学术语之外的任何措词。但是我极力主张数学家和其它科学家在评估康托尔结果如何影响传统无穷大概念时应用起来应比惯常更加小心谨慎。看来无穷大仍然还是我们力所不及的。
[Scientific American,1995年4月号]
____________________
* A·W·Moore是牛津大学圣休学院哲学研究员。他的主要学术兴趣在于逻辑学、形而上学、康德和维特根斯坦(英国哲学家、数理逻辑学家)的哲学。所有这些都渗入到他有关无穷大的著作之中。