唐豪
上海交通大学物理与天文学院副研究员
金贤敏
上海交通大学物理与天文学院长聘教授,集成量子信息技术研究中心主任
模拟研究是一个大家并不陌生的研究手段。例如侦探在推理案发现场时,往往会采用近似的替代物来尝试复现当时的经过,因为不可能让真实的原人物重演。又如科学家研发飞行器时,会在风洞实验室里人工产生并控制气流,用来模拟飞行器的运行,因为如果研究真实飞行器,一旦坠毁则成本代价太高。模拟研究使得这些不可能或者太难办的问题变得可能。
量子模拟同样具有这样的目标。20世纪以来,人们认识到世界不能只用经典力学来解释。小到凝聚态物理中的电子运动的特性,微生物体中的能量传输,大到宇宙中的黑体辐射,都不能忽略量子效应。这些从微观到宏观的自然万物,直接观测往往非常困难,如果采用经典计算机进行模拟分析也并不乐观,例如计算多体量子系统,需要消耗指数级的资源,模拟50个自旋粒子组成的多体系统需要计算量高达250量级,让现代最先进的超算望而生畏。1980年初,诺贝尔物理学奖得主理查德 · 费曼(Richard Feynman)提出,是不是可以用一个人工构建的量子系统去模拟自然界中的量子系统呢,这样一来只需要多项式级的计算资源了,使研究原本不可控或者难以实现的量子系统变得可能。
费曼提出这个量子模拟(Quantum Simulation)的思想,并在几年后他类比经典计算机基于逻辑门的数字电路,提出通用量子计算机量子线路的构建。不过,量子模拟既可以采用这种将量子系统编码到量子线路的数字(Digital)型方式,也可以采用初始提出的直接用一个现成可控的量子系统去类比待模拟的量子系统的类比(Analog)型方式。两种方式都在实验中取得进展,尤其是近五年来,基于冷原子、离子阱、超导、光子等不同量子物理体系的量子模拟都在快速推进。量子模拟的意义正在加倍凸显。通过不断发展的量子模拟实验技术更准确地模拟了解从微观到宏观的自然万物,使人类对科学和世界的认知得到加深与升华。
量子模拟的三板斧功夫
量子模拟研究各种复杂的量子系统,听起来好像很难。其实再复杂的功夫都有特定的武术招式,量子模拟概括来看,只包括三板斧的主要步骤。首先,需要制备好最初的量子态|ψ(0)〉,比如指定纠缠的粒子对从哪几个特定入射节点注入。其次,也是最核心的一点,需要制备好量子系统的演化空间并实现量子态的演化。量子系统各节点怎样相互耦合的情形,在物理上我们用哈密顿矩阵来描述。量子模拟便是将待模拟系统的哈密顿矩阵Hsys映射到实验室构建量子系统的哈密顿矩阵Hsim中。量子态在这样空间中的演化符合微分方程的描述,通过幺正操作U=exp{-iHsimt}就可获得时间t时的量子态波函数|ψ(t)〉。第三个主要步骤是对该量子态相关信息进行测量,从而获得待模拟系统的定量或定性的认知。
由此可见,方便地制备量子初态、实现大规模且可精准操控的哈密顿矩阵及幺正演化、方便测量的能力是实验开展量子模拟的重要考虑因素。
前面提到数字型的量子模拟,这种通用量子线路实现哈密顿量的映射构建,需要将待模拟的哈密顿矩阵分解到一个个量子逻辑门中,时常还需要采用Jordan-Wigner等各种变换方法将哈密顿量进行转化之后才能对应到量子线路中。通用量子线路上进行幺正操作,也往往需要采用Trotter-Suzuki近似等近似方法才得以实现。此后对通用量子线路的演化结果进行测量,需要对各子项进行换基测量。完成这一系列操作实现特定量子模拟,往往需要成百上千个量子比特构建数以万计的量子逻辑门,再考虑到这些对于精准量子纠错的极高要求,因此在目前中等噪声量子技术时代下颇具挑战。
而前面提到的类比型量子模拟,不采用通用量子逻辑门,而是专门构建一个量子系统整理,直接与一个特定系统的哈密顿量进行映射、解决一个特定问题,好比针对每种机型专门定制对应的飞机模具进行研究,而不是采用通用的乐高积木组装出所有机型模具。因这种专用性,类比型量子模拟也常称为专用量子计算。这种量子模拟方式不只在哈密顿量的映射上更加直观,而且该量子物理系统的自然演化天然地实现了哈密顿量的幺正操作,好比飞机模具在风洞的飞行可以自然对应飞机的飞行,而不需要在通用乐高积木组装的轨道中近似模拟飞行。此外,类比型量子模拟也更加方便测量获得演化后的量子态信息。相比数字型量子模拟,类比型量子模拟可减少对量子计算资源及量子纠错的要求,在多种量子物理体系都有所实现。
以光子体系为例演示类比型量子模拟的三板斧功夫。光子具有速度快,受噪声或消相干影响小等优点,并且集成波导阵列极大拓展了光学量子模拟的灵活性和可扩展性。首先,多光子技术可以方便制备量子态的初态,例如通过将波长为405 nm的光子射入一种晶体,激发生成一对810 nm的纠缠光子,光的能量与波长成反比,因此总能量仍得到保持。多光子可带来经典无法模拟的量子相干等特性。
然后,通过三维光波导阵列构建哈密顿量及幺正演化。哈密顿量可以做到非常大且高维,以量子行走(Quantum Walk)这一专用量子计算重要工具为例,此前在其他量子物理体系中进行实验演示量子行走时,往往只能在一维的格点中进行若干步的原理性演示,而基于三维光子芯片,构建了49×49个节点的大型二维演化空间,实现了首次真正空间二维的量子行走,推进专用量子计算的实用化。并且通过波导的各种调控可实现对哈密顿矩阵的精准操控,为实现各种特定波方程的量子模拟提供了丰富的可能性,例如通过随机设置波导空位模拟量子逾渗,通过周期性弯折波导实现光子传输动态局域等等。三维光子芯片波导阵列的横截面构型反映了哈密顿矩阵的特征,而波导的纵向延伸长度则对应了光子的演化时间,因此光在波导中的演化直接对应实现了哈密顿量的幺正操作,且演化时间长短精确可控。
之后,测量演化后的量子态相关信息则可通过光子成像及探测技术采集光子在波导终端的分布情形获得。对于激光即相干光演化用普通电荷耦合器(CCD)相机就可以拍到成像,如果要对晶体泵发出的一个个单光子的演化结果进行成像,则要用到增加了图像增强管的增强型电荷耦合器(ICCD)相机。单光子的演化结果像投标枪的靶一样,每次落点都不一样,我们不停地发射单光子并累积一段时间,就会呈现出现律性的光子累积概率分布。
量子模拟洞悉电子微粒与星辰大海
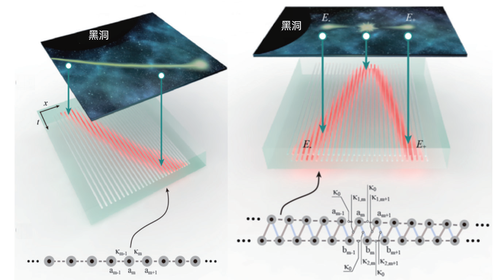
世间万物,极大与极小就如同探险家眼中的珠穆朗玛峰与马里亚纳海沟一样,显得神秘、富有魅力,却又难以企及、充满挑战。例如,在宇宙学中,虽然目前仍无完整的量子引力理论,但弯曲时空中的量子场论可以用来描述量子效应不能被忽略情况下的引力,如发生在具有强引力效应的黑洞视界附近的粒子加速以及霍金辐射。霍金辐射指由于真空的涨落,粒子-反粒子对在黑洞的视界附近产生。负能量粒子落入黑洞,而正能量粒子逃逸出黑洞引力。从黑洞外部观察者看来,好比黑洞刚刚释放出一个正能量粒子,并失去了质量。但由于现有技术的限制,我们仍无法近距离观测黑洞各类极端天体以及其附近的量子演化行为。
好在现在多种实验室系统都能开始尝试模拟宇宙学,尤其是变换光学,它通过操纵材料的介电常数和磁导率设计多种具有新颖光学应用的人工系统,模拟广义相对论现象:黑洞、爱因斯坦环、宇宙弦、虫洞及宇宙膨胀和红移等。实现这些模拟的基本原理都是复杂非均匀介质和任意时空度规背景下麦克斯韦方程的形式具有不变性。因此我们基于变换光学理论,采用飞秒激光直写技术制备波导耦合系数沿横向逐渐增强的三维波导阵列,对应复杂非均匀介质下的麦克斯韦方程,从而构建人造黑洞视界附近的引力场。观察单光子波包所代表的粒子的量子演化呈指数加速形式,且其指数取决于黑洞的曲率,区别于平坦空间中的粒子的线性运动,这就模拟了粒子在黑洞视界附近的加速现象。此外,通过设计双层光子波导晶格,还可模拟黑洞视界处费米子对的产生和演化:一个正能量的单光子波包从黑洞引力中逃逸出的负能量的单光子波包被黑洞捕获。这种现象呈现出正能量粒子从黑洞逃逸出的效果,正是对霍金辐射的模拟。
光波导阵列模拟人工黑洞弯折空间的粒子加速运动以及费米子对的霍金辐射
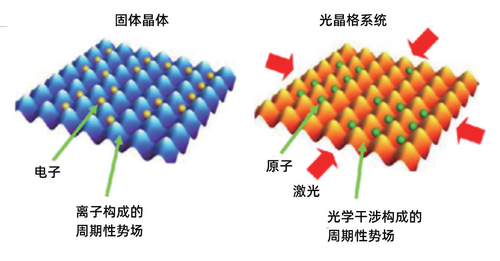
量子模拟的还有一个广泛的应用场景是模拟凝聚态中电子的运动。这些电子围绕着的原子核之间不到纳米级间距,电子又在高速运转,很难在实空间里观测到电子在哪儿了、怎么运动的、电子自旋之间是怎样关联的,等等。而这时基于冷原子的量子模拟就派上用场了。它的装置结构就像平时装鸡蛋的纸壳,可以把鸡蛋牢牢放在一个个坑里稳稳的。这里的鸡蛋壳就是光晶格的光场,鸡蛋就是原子。原子用激光冷却后加载到光晶格形成的势场中。原子在光晶格里的分布变化可以模拟电子的行为,好处在于原子的运动比较慢,光晶格的间隔也相对较大,约为几百纳米,可以方便观察到原子的分布运动。高中理科生都知道任意物体都既是粒子又是波,它的德布罗意波长与动量(即速度乘以质量)成反比。激光冷却原子时,原子的动能降下来,德波罗意波长变大,所有原子几乎都符合一个统一的波函数。这种德布罗意波长远远大于晶格的情形使隧穿等量子效应不可忽略,凝聚态中的电子的波长也远远大于凝聚态中的原子核之间的间距。这也正是冷原子类比模拟电子运动的原理所在。
光晶格中的原子运动模拟凝聚态中的电子运动
值得一提的是,冷原子不止用来模拟电子,光波导阵列也不止模拟黑洞视界。每种量子物理体系都可以通过哈密顿量的合理映射实现广泛的量子模拟。
量子模拟助推算力极限
从一定意义上说,量子模拟是一种量子计算,尤其是类比型量子模拟,往往被称为专用量子计算。这是因为量子模拟实现经典计算机需要耗费巨大资源才能模拟的问题,例如开头提到的50个粒子的自旋链的计算问题,量子模拟器有望实现指数级加速。还有玻色采样问题,许多光子(即玻色子)从多个入射口注入光学网络,通过各种设定的分束器和相位调制器的参数,构建出光学网络实现符合哈尔随机的幺正变化,然后试问光子在出射端的分布情况。这个幺正操作的矩阵根据光学网络参数确定后,玻色采样结果可以通过经典计算机计算,但是涉及积和式的计算,运算量非常大。此前,上海交通大学与国防科技大学合作动用了当时(2013—2016年)一度排名世界第一的超算天河二号的全部算力,计算50个光子的玻色采样还需要100分钟。好在玻色采样是一个天然的量子模拟问题,想知道乒乓球落地后弹几下,何需估算摩擦力再带入公式努力计算,直接投个乒乓球就好了,光子怎样分布,直接将多光子导入这个光学网络实现天然的幺正操作再测量出来就可以。但是这在实现上需要非常精细的调节,这也正是76光子的玻色采样机“九章”在今年问世以后带给全世界学术圈很大震撼的原因。九章实现专用量子计算硬件上的前沿突破,体现我国在该科学领域的分量,值得为之自豪并持续奋进。
由量子模拟推动计算复杂量子物理体系问题的功能延展开来,量子模拟不只可以帮助加深基础物理的基础研究,还可以成为普适的计算工具,因为这些映射的哈密顿量还可以进一步映射到人工智能、金融、信息技术等广泛信息技术领域。比如,模拟神经网络的联想记忆功能,可以进一步演示这个功能在图像识别中的应用。又如当初只是为了展示量子加速优势的玻色采样,未来也会在图论、机器学习、量子化学等领域具有重要的潜在应用价值。此外,通过量子模拟的实验技术手段实现量子信息处理的各种功能元件,例如,如何在集成量子系统里存储量子态波包,如何在大规模网络中完美传输量子态等等,也会通过推动量子信息技术本身的发展来促进应用探究。
因此,当前需要充分发挥并发展量子模拟的实验技术能力,在可操控维度和精度上达到一个新的高度,实现广袤世界万物的精确模拟,并延伸到生活各领域的应用探究,推动实现一个更精彩的世界。