生物节律的原因,可能在于化学反应的有规律的振荡。化学反应实验常常发表在一些无名科学杂志上,正在揭示自然界迷人的规律。
二十年前,在一次不引人注意的俄罗斯讨论会上,苏联化学家B. P. Belousov提出一种惊人的新化学反应。这个反应,使浸在水里的有机燃料,在室温下氧化成二氧化碳和其他一些物质。燃料可以是所有活细胞中的任何简单分子,丙二酸盐、柠檬酸盐或苹果酸盐等。在活细胞中,催化剂将调节反应。但对多种氧化/还原酶,催化剂原来是一种过渡金属离子——铁或铈。反应最显著的特征是,反应脉冲极其规律,间歇时间约为一分钟。(注意:反应物应处于同相,如液体——即均相反应。)在溶液中使用适当的染料,可以见到红——蓝——红——蓝……颜色的交替变化。反应振荡非常明显。
在1959年,这虽还被当作是一种奇谈,但毕竟也可算是一种预言。曾做过保险公司计算员的理论家Alfred. J. Lotka,在1920年,就曾因公开预言振荡反应而遭人嘲笑。但是,Belousov却用普通的均相溶液,第一次令人无可置疑地证明了这个反应。这个反应,直到1970年之后才为西方所知。
七十年代,不同背景和抱有不同目的的科学家们,对这个反应是如此的感兴趣,以致讨论化学钟动力学及物理化学学的英语文献,像先前的俄语文献一样一下子爆发了出来。
这幕闹剧发展的第一阶段,是根据经验来调整溶液化学组成,增强这种反应的唯一特征。这事实上,在六+年代,已由A. M. Zhabotinsky和他的朋友们解决了。1968年,在布拉格一次由欧洲生化学家协会召开的有关生物钟的讨论会上,作者有幸会见过Zhabotinsky。在那时,反应还只能靠紫外比色计来测定。1969年,Zhabotinsky和德国的Heinrch. Busse提出改用丙二酸、无机盐及一种铁的有机络合物作催化剂和颜色指示剂,既十分可靠,组成又简单。
1970年,A. N. Zaikin和Zhabotinsky又发表了他们的另一重大改革:这种组成,不但振荡均匀,且发出表示氧化活度的鲜明的蓝色波,就像在草原上延烧的火一样(但如科学史上所经常发生的那样,这个现象,在前一年已分别由Busse和Marcelle Herschkowitz-Kaufman真实地拍摄下来,并且发表了。但是,他们二人对此作了极不相同的解释。这种解释,现在是已被人抛在脑后了。一种新的思想,导致了理论的健康发展。)
七十年代早期,Richard J. Field、Endre Koros、Richard M. Noyes等人,根据对包含氧化还原周期的一系列反应的详细分析结果,对Zhabotinsky和Hans Degn提出的化学机制,继续进行了研究。他们把错综复杂的因素归纳为三个相互作用的因子:相应的溴离子浓度、亚溴酸浓度及金属离子催化剂氧化百分比。有关的微分方程式,即是大家所熟的俄勒岗振荡器。俄勒岗振荡器能更好地显示循环周期的存在、波形以及周期时间与各不同组成间的关系。在加入表示分子扩散项后,还能显示波的存在,以及波速与化学参数间的关系。
1975年,Field从俄勒岗州的Eugene来到宾夕法尼亚州的匹兹堡。在那里,会见了数学家William Troy,并共同开始对丙二酸反应的另一种现象进行研究:不是反应的自发振荡而是其“兴奋性”。1972年,作者曾用实验证明,如果把化学组成限制在抑制振荡下,波的行为是否消失?结果是,多数生物振荡器,只要稍微改变一下某化学浓度下的温度,即可把该自发振荡器(“钟”)变成一局部稳定系统(“沙漏”)。这种系统存在,而且只存在一个周期,除非有破坏平衡的足够干扰。这证明,Zhabotinsky的组成法是可行的。不过,使作者惊奇的是,反应物继续显示与初始刺激完全一样的波形。这时,只要原先刺激没有超过阈值,刺激主要是由于化学反馈而放大。在这方面,丙二酸的反应与活神经膜的电兴奋性非常相似,1976年,Troy和Field、从数学上证明了俄勒岗振荡器和神经膜电子/离子方程间的相似性。Alan Hodgkin和Andrew Huxley曾因神经膜的离子方程而荣获1963年度诺贝尔奖金。
适于化学和可兴奋活神经膜的最引人入胜的原理之一,是从近年来对起搏神经细胞的研究中得出的。与俄勒岗振荡器一样,Hodgkin-Huxley方程也描述了数学家们所称的“引力极限周期”。这是一个浓度变化完全连续的反复过程。系统几乎是自发的,从所有初始状态趋向于这一变化。(“所有”一词有一定限度。某些例外,在下面是非常重要的。)如用瞬时化学刺激中止振荡器的引力周期,振荡器便立即回复到原周期,并按这周期精确地振荡。干扰只产生了一个后效:节律的相位变化。如果振荡器是处于其振荡周期,那么刺激就把它变到一个新相位。在这意义上讲,当正常节律恢复时,刺激好像是临时变动一下振荡而已。
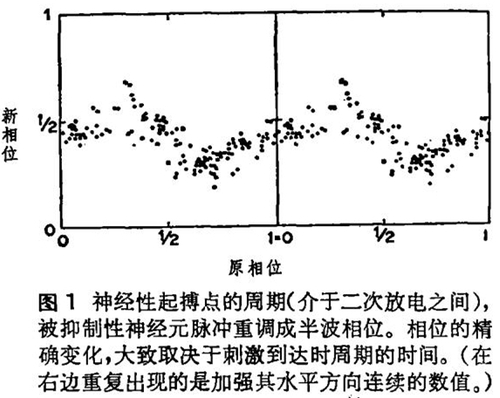
神经起搏细胞对任一给定刺激的新旧相位曲线,可通过Hodgkin-Huxley方程建立。作者的学生Eric Best,在珀杜完成了这个工作。而差不多在同时,Daniel Hartline、Harold Pinsk-er Jose Jalife等人也分别独立地对真实神经细胞进行了同样测定,且获得了同样独特的模式。(图1):当刺激前的相位扫描一个周期时,刺激后的相位才开始升起,但不到一个周期即平滑地跌下了。(但是,这仅发生在刺激量至少是处于某一最小量级时。显然,极小的刺激是不能获得这个模式的:它们的相位基本上不变。)
若不仔细想想,你定以为这个结论是对的。但是,这里有一个令人含糊的问题:即振荡器必须有一定的条件,即所谓“无相位”或“全相位”。非振荡状态会成为一个连续波的波源。在看具体例子之前,可能会觉得这点疑问是可笑的。理由基本上是属于拓扑分布上的。
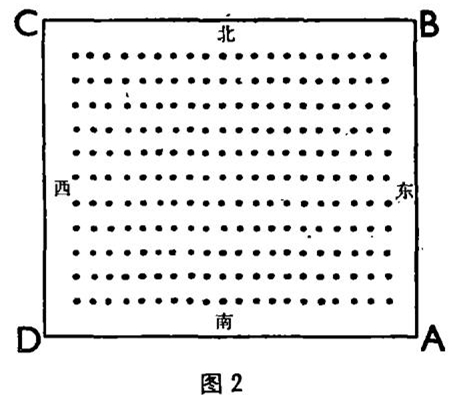
假如,我们把起搏细胞、一小块心脏肌肉,或者一滴振荡试剂,按东西为列、南北为行,依次在桌上排成一方块(图2)。这样计时,即每一行同步,且比邻边的西边一行相位稍许置前一点。这样,得到了从西到东的一个相位梯度,并精确地组成一个周期。然后,从南到北,按一定量级同时给予刺激。每一行南端,加入的量少到可忽略不计,而逐次增加到北端达到相当大的量级。之后,沿着方块北面一边(BC),从东到西进行测量。发现,原相位的变化,不是增加了,就是减少了,但是没有超过一周的。再后,再顺西边(CD)继续测量。沿着这行,看到了刺激量逐次减少的影响,相位全部为0°(=360°)。不管如何观察,在东边(AB)也获得了同样结果。相位全部为360°(=0°)。所以,从A→B→C→D相位并没有减少或增加。即使沿着这条线路,相位可能增加。但是,反过来,减少值又正好等于该值。
现在,按方块的逆时针方向,沿刺激量为0的南边,从D到A进行测量。发现,新的“重调”相位,几乎与以前刺激未加入时一样。这样,我们测量了相位的一个周期。净效应是,新的重调相位,沿着方块的边增加了整整一个周期。这是一个拓扑分布的结论,非常正确,与线路上任何微小的定量上变化完全无关。只要新相位是随刺激时间不连续地变化,新相位就严格地取决于旧相位。这说明,沿着方块的顺时针方向,会不断地出现周期的任何一个相位。在振荡的一个周期内,波精确地顺方块循环,并再次重出现在起始点上。
兴奋波就这样沿方块不断循环。这种化学钟,每一行要素的脉冲是周期的,但却不是同步的。周期取决于旋转脉冲的循环时间。那么,哪里是旋转波的波源呢?没有。像追逐自己的尾巴而团团转的游戏一样,旋转波绕一中心点旋转。所以,旋转中心点,似乎也就成了所有相位的组成部分。但是,作为旋转中心,又必须处于不变的无相位。
是不是所有情况都是如此?是的。凡化学反应,都发生振荡。神经、心脏、大脑等可兴奋组织是这样,其他生物钟也是这样。这里,我们触及了多年来使物理学家、物理化学家、数学家等特别感兴趣的一些领域。虽然,对旋转器至今了解不多。但是,几十年来发现的一些例子(包括最新的“发现”),对于科学文化总是多少值得庆幸的贡献。
第一次在真正实验系统中,对绕中心点旋转的旋转波的观察结果,1963年发表于日本。Jin-ichi Nagumo,Ryoji Suzuki及S. Sato等人,在东京一直研究引人注目的类似神经的氧化波。该波于浸在硝酸里的铁丝上传播,采用电化学刺激起激。Nagumo小组认为,浸在硝酸里的铁丝网,可能具有像大脑、心脏等可兴奋细胞二维薄片所具有典型的、类似波振荡那样的特有模式。只要一开始就使用适当的电化学刺激,就可产生连续的旋转波。每个波都绕一电化学相位的中心点旋转。
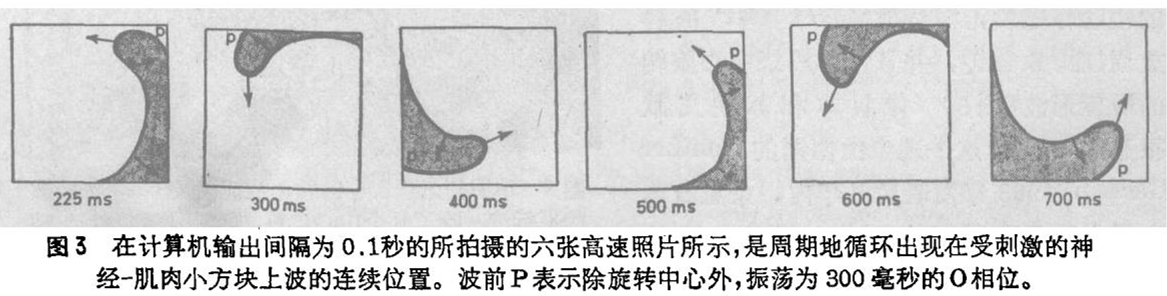
与这篇论文毫无关系,九年后,F. B. Gulko和A. A. Petrov在苏联发表了同样的报告。他们用数字/模拟混合计算机,对按二维排列的细胞的Hodgkin-Huxley方程进行了修正。从数学的角度,用不同的刺激来观察旋转波的形成和存在。使用与前面实验相同刺激时的结果,如图3所示。
这二种实验都是为了检验那个未经证明的概念,即心室纤维性颤动——致命的心脏“心律不齐”,也许正是波型在拓扑分布上的变化:由窦房结发出的正常圆形波变成以心脏任何一点为中心的螺旋波。这种波,会使心脏肌肉的每一点都发生节律性收缩,但却不是同步的。这样,泵的动作就变成了无益的搅动。Nagumo和Gulko的实验,证明这个结论是正确的。
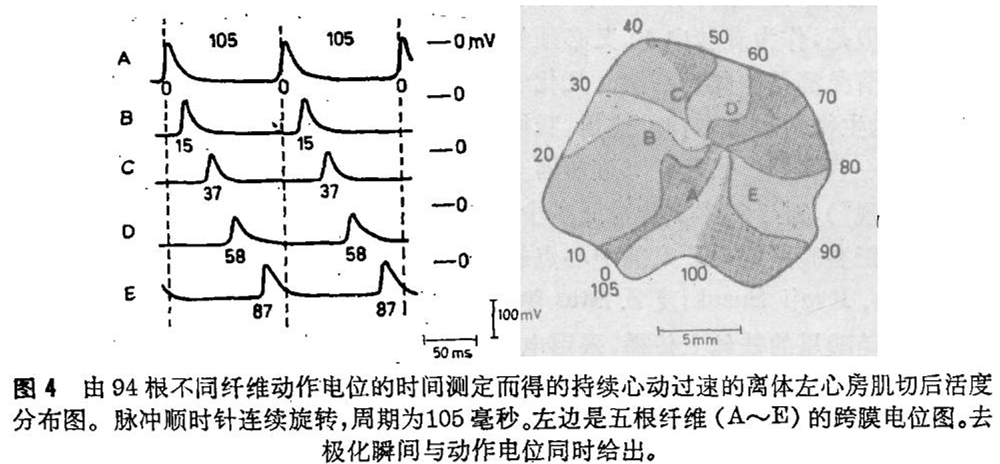
与上述二篇文献无关,荷兰的Maurits A. Allessie、F. I. M. Bonke和F. T. G. Schopman对兔子心脏肌肉作了一次直接试验。有关详情,恕不赘述。独创性的实验布置,也使用了在上述实验中获得成功的相同刺激,得到的是有害的稳定旋转波。图4是其中一例。对无损伤的、具有正常机能的心脏来讲,这样的波会使保持血液循环所需的节律性收缩全部搅乱。如发生这种情况,那么死亡也即来临了。
几乎在同时,苏联的A. N. Zaikin和Zhabotinsky对丙二酸二维薄片的类似波型也进行了研究。Zhabotinsky的论文(1970年发表于苏联)报告说,用与上述相同的立体型化学刺激,也得到了相似的振荡旋转波。这种旋转波,一经形成即非常稳定。并且,立即影响了整个反应液的其他所有波源。
从物理化学观点来看,特别感兴趣的是旋转器的中心点。这是螺旋波的静止波源,并且周期性地在空间上或时间上构成了整个反应。但是,旋转中心本身的振荡却并不规则。一种理论认为,旋转中心具有认为是造成胚胎细胞分化不同空间结构的类似横向浓度梯度。
事实上,一个机体组织的形态,主要是取决于化学振荡。一群阿米巴Dictyostelium discoideum,在其环化 - 磷酸腺苷(CAMP)——激素的“第二信使”的新陈代谢中,极易振荡和兴奋。Earl Sutherland曾由此而获得了1971年的诺贝尔奖金。由显微镜拍摄的慢动作电影,清楚地显示CAMP的释放周期为5分钟,并且常形成绕中心旋转的螺旋形波(图5)(像日本和苏联文献报道的一样,这个现象由德国的Gunther Gerisch1965年发表后几年内,未见有英文报告发表)。每个细胞都向邻近的波趋近,最后集聚在中心点周围,形成一种多细胞组织。然后缓缓移动,完成一个生命过程。
Albert Goldbeter和他的朋友们,最近提出了CAMP合成和降解的动力学,显示了上述化学钟内的兴奋性和引力极限周期。Malehow和他的朋友们,最近测得了CAMP脉冲(从通波上)对同步振荡细胞相位的影响,并获得了与上述起搏神经细胞及心脏浦金野氏纤维相似的重调相位图。从这一方面或其他方面来看,形态发生的原始组织激素法似乎成了神经系统的最早母体。
若用垂直纸面的第三根轴来表示时间,可以重画似图3、图4那样高速照片。这只要简单地把一连串旋转波的高速照片,顺轴依次排列即可。当波绕轴旋转时,随着时间的增加,波前就扫描出一个螺旋面。这时,每一处的横坐标表示其初始相位,和作用于该相位的刺激量,纵坐标表示波前到达该处的时间,即局部节律的重调相位。
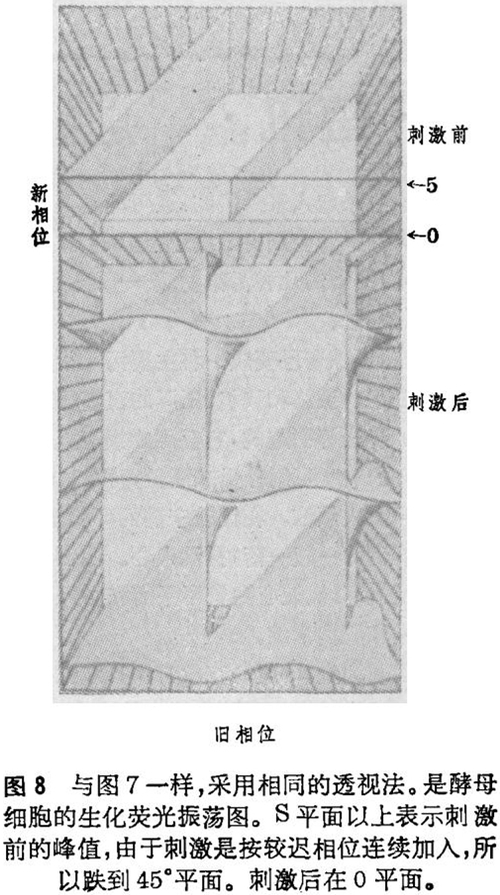
精确测量的方法,已由生理学家根据刺激时间对心跳、支配组织日夜盛衰的24小时生物钟,及单细胞中糖代谢的半分钟振荡等节律的相位控制影响而系统地加以总结。例如,图6是果蝇生物钟对光脉冲时程及生物钟原始相位重调相位图。图像是一往上卷起的螺旋面。图7是Wolfgang Engelman根据在户外对花朵24小时节律观察的结果所画的数值。图8是作者在绝氧条件下,对酵母细胞糖类无氧代谢的生化荧光节律的测定结果。刺激采用氧脉冲。由一片薄标本(原始相位、一定剂量的氧)测量结果表明,按图2所示方法进行单独的大型实验,会产生绕固定中心旋转的绿色荧光波。根据Goldbeter的理论,控制糖类新陈代谢节律的酶方程式与控制阿米巴群CAMP振荡(和螺旋波)的完全一样。
由图6、7和8可知,只有刺激时间和刺激量精确配合,才能产生唯一效果:节律既不超前也不滞后,但却逐渐消失了!对果蝇来讲,生物钟似乎在发育卵中即已形成,在机体组织第一次碰到使生物钟开始走动的光或温度变化以前,就开始振荡了。对酵母细胞来讲,临界刺激似乎是使糖类新陈代谢达到理想的动态稳定的调节机制。对果蝇和高凉菜属花来讲,极微量的干扰就会重复以前的振荡。
各类化学钟中,存在着一些共同的原理。这些原理,大体上是属于拓扑分布的。定性分析表明,相位角会在空间上或时间上发生变化。且揭示,在一条件下,必然存在一点,且唯有在这一点上,相位显然是不受限制的。即使是支配各处规则循环的振荡器,在这里也必然失败。这—点常成了空间、时间结构上的中心。
人类到现在才开始有意识地探讨这些原理。但是,在几万万年前,人类在生活的各种自然选择过程中,已无意识地发现和揭示这些原理了。对丙二酸的研究,使我们第一次对相同的拓扑分布的压制因素有了一定的概念,反过来也有可能对其作更完整的分析。由于这个活动在1970年后才真正在全世界范围内开展,所以肯定尚未达到至臻完善的阶段。
[New Scientist,1978年10月5日10 ~ 13页]