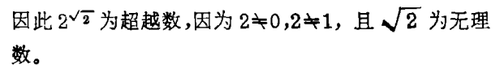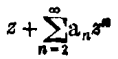突破1：四色定理

大家都知道四色问题，不过，我想先提出一些以前你可能从未找麻烦问过自己的初等问题。这些问题涉及欧几里得平面，该平面的拓扑学展示出某些出乎意料的、神秘怪诞的现象。

比如，你知道在平面中存在具有共同边界线的5个区域（瓦达（Wada）湖）吗？用“2个”代替“5个”时，每人都明白：只需回忆一下右半平面和左半平面，即用笛卡尔坐标的术语，具有正X坐标的点集和具有负X坐标的点集。这里共同的边界线是y轴，丝毫没什么奇怪的。顺便指出，“区域”一词的含义类似于复变理论第一堂课所讲的：开的连通集。3个区域具有一条共同边界的情况怎样？能举一个简单的例子吗？不能。只要能建构3个区域具有共同边界线的例子，那么5个的例子也容易建构，甚至任何有限个也都能办到。

这是否意味着四色问题的负解（即反例）？6个区域在平面地图上代表5个国家，因为其中每两个在其共同边界线处接壤，所以给地图正确地标上颜色的唯一方法是使用5种不同的颜色。

不错，这是四色问题的一个负解，但只是由于问题的提法不严格造成的。如果5个区域有一共同边界线，则这些区域和它们的边界线必须以极其别扭的方式扭曲、联锁在一起。经典四色问题（通常心照不宣地）假设地图上的国家都是健康的，不是病态的。排除病态的一种简单方法是要求国家的边界线是多边形（有限个小曲线的片段）；即使在如此强的限制情况下仍然保留着问题的全部深度和困难。如果这似乎太严格了，那么允许边界线是体面的连续曲线也行，但某种几何上的限制是必要的。

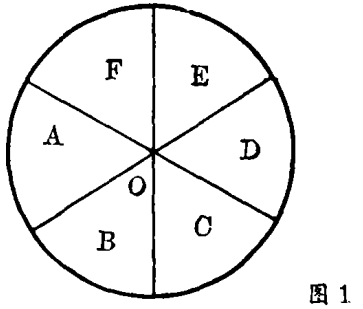
另一个有启发性的例子是看一个圆形地图，在其中画几条直径（比如三条）。这些直径把地图分成6个国家，所有6个国家都在圆心“接壤”。这是否意味着需要6种颜色为地图着色？并非如此。四色问题中说的共同边界线应有一定长度，即“接壤”排除了尖角、孤立点的情形。

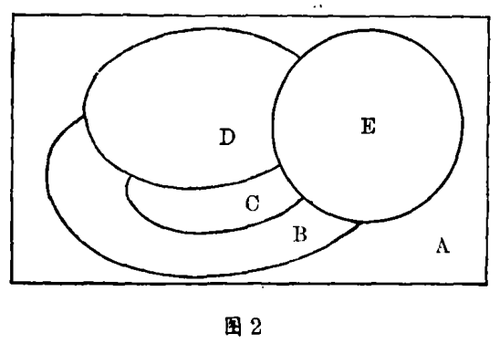
那么，为一幅正常的地图着色所需的最少数目的颜色是多少？2种、3种颜色都不够。5种颜色实际上足以（1890年已严格证明这一点），如图2所示。1852年格思里（F. Guthrie）提出如下猜想：对平面或球面上的任一地图着色，至多用四种颜色就可以使两个相邻（即有一段公共边界）的国家或区域的颜色不相同。

四色问题可用图论语言表述，若用点表示区域，用边表示区域的相邻关系，则四色问题即为任何平面图的点色数不超过4的问题。1976年阿佩尔（K. I. Appel）和哈肯（W. Haken）声称利用电子计算机证明了四色猜想。

最后说一句，突破（explosion）意味着一种大的声响，一则出乎意料的通告，但不一定是件好事情。某些突破开辟了新的领域，在未来有广阔的发展前景；另外一些突破关闭了一个领域并且似乎并未开辟新天地，下面要讲的突破莫德尔（L. J. Mordell）猜想是第一

类；四色定理是第二类。

参考文献：EDM165。

突破2：莫德尔猜想

每个小学生都知道9+16=25，或者换种表述有3²+4²=5²。转念一想便知道3、4和5用3k、4k和5k（无论K是什么数）代替方程仍然成立。如果想找方程x²+y²=z²的整数解，实际上不必区分3、4、5和6、8、10两组解。可以把问题转化一下，方程两边除以z²得(x/z)²+(y/z)²=1，用x和y代换x/z和y/z，方程变为x²+y²=1。这样原来要找的整数解就变成找有理数解。

方程x²+y²=1有许多有理解，无穷多个，用几何的语言说，方程所定义的曲线上有无穷多个有理点，那些点与所谓的毕达哥拉斯三元组有关，并很容易找到。这种情形不同于著名的费马问题。费马问题试图证明，若n＞2，则由方程xⁿ+yⁿ=1定义的曲线在其上根本没有有理点（除了平庸情形：x或y有一个为0）。

费马问题属于莫德尔1922年提出的更广泛的一个问题。莫德尔在阐述这一猜想时天才地使费马问题同时变得很难又变得简易。前者因为他扩大了所考虑的曲线种类，包括了实数域上亏格（genus）大于1的所有代数曲线；后者因为他放松了所要得出的结论，允许存在有理点，但个数为有穷多个。莫德尔猜想已不再是一猜想，1983年德国数学家法尔廷斯（G. Faltings）证明了这一猜想，获1986年菲尔兹奖。但费马问题仍悬而未决。（莫德尔猜想为：在亏格大于1的代数曲线上仅有有限个有理点）

参考文献：MI6/2/41。

进展1：遍历理论

上世纪玻尔兹曼最早提出遍历假设，通俗点说，这一假设认为台球在桌面上的运动最终可以通过台球桌面的每一点。懂点拓扑学知识就会发现这个假设是错误的。但原来的假设可以修改为准遍历假设：虽然台球不能通过所有点，但可以充分接近每一点，也就是说，它在台球桌面上处处稠，1931年伯克霍夫（G. D. Birkhoff）证明台球经过某区域的时间正比于该区域的面积，并且与台球的出发点无关。而（准）遍历假设是其推论。目前遍历问题已发展为专门的数学理论，内容极其丰富。许多学者在这一领域做出了杰出贡献。

参考文献：EDM146/B

进展2：超越数

如果不是，那么它至少是代数数吗？（代数数是整系数多项式方程的一个解。）希尔伯特的第7个问题就与此有关。什么时候α^β是超越数？若α=0、α=1或者β=0、β=1，则此问题已退化。如果β是有理数，则问题变为比较容易的有关代数数的小问题。另一方面，如果α或β是超越数，要找的答案与已知条件又太接近了。考虑了这些评注，问题的“正确”提法为：若α和β都是代数数，α不为0和1，β为无理数，那么α^β是超越数吗？回答是肯定的。1934年盖尔丰德（A. O. Gelfond）和施奈德（T. Schneider）近乎同时独立地对希尔伯特第7问题作出了肯定回答。

此理论并未就此结束，贝克（A. Baker）60年代后期发表一系列论文，作了n重推广，因此获1970年菲尔兹奖。若α₁，…，α_n是不同于0和1的代数数，并且若β₁，…，β_n 是使得1，β₁，…，β_n，在有理数域上线性无关的代数数，则α₁^β1，α₂^β2，…，α_n^βn是超越数。超越数论正使用着交换代数、代数几何、多复变函数论、甚至上同调理论的方法，目前仍十分活跃。

参考文献：EDM414/D。

进展3：连续统假设

1900年在巴黎召开了国际数学家代表大会，希尔伯特在大会发言中提出著名的23个问题。其中第1个就是康托最早阐述的连续统假设。康托连续统假设的最简单的陈述是，实数的每一不可数集一一对应于所有实数的集合，或者用康托的术语来说，在阿列夫零和2的阿列夫零次幂之间不存在基数。

连续统假设正确吗？这个问题很类似于欧几里得的平行公设。这两者都有多少比较满意的公理系统（在这里它是集合论的E · F · F · 策梅洛 - A · A · 弗伦克尔公理系统）和不太令人满意的、更复杂的、不太显然的附加公理。如果这个附加公理是基本公理的一个推论，则它是真的，一切都好办；如果它的否定是基本公理的一个推论，则它是假的，不论好坏，问题总算有了确定的回答。期待已久的答案便成为一项精致、深刻的智力成就。哥德尔1940年（亦说1938年——译注）证明，连续统假设不假，即它与其它集合论公理相容；1964年（亦说1963年——译注）柯恩（P. J. Cohen）证明，它不真，即它独立于其它公理，或者换种说法，它的否定也是相容的。

哥德尔和科恩都采用了适当模型的构造性方法，但使用了很不相同的技术。哥德尔从一个满足ZF公理的一个全域集合出发，证明存在一个同样满足ZF公理的一个子域，并且在其中连续统假设为真，科恩的论证与此相似，但更艰难。它使人们想起T巴切夫斯基平面的F · 克莱因建构（赋予欧几里得圆盘一种新的度量）。像哥德尔一样，科恩由集合论的一个模型开始，然后扩充它，把新的对象复合上去，用这种方法“迫使”连续统假设为假。“力迫”（forcing）方法已成为这一领域的一种重要技术。

那么连续续假设被置于何地呢？与蜀德尔类似，许多人相信它在某种合法的意义上或者真或者假，尽管它有独立性。人类仍未想到描述集合论全部真理的恰当方法，一旦全部真理都已知道，一旦适当的附加公理被找到，并复合到目前的公理系统上，则连续统假设将变得或者可证或者不可证。两种学术观点都存在，你可以自由加入你觉得有吸引力的一派、如果你知道哥德尔相信哪种观点，这会影响你的选择吗？他认为连续统假设不可证。

参考文献：EDM35/D

进展4：李群

希尔伯特的第5个问题问，关于拓扑群的某些相对温和的假设是否足以蕴涵很强的结论，拓扑群是同时具有群结构和拓扑空间结构的集合，在其中两种结构某种意义上（群运算连续）是相容的。

一个典型例子是由形式

构成的所有2×2矩阵的集合，其中x＞0；拓扑结构是右半平面结构（x＞0的所有（x，y）），乘结构是与矩阵有关的通常的结构，这个例子有一重要的特殊性质：它是“局部欧几里得的”，每点都有一邻域同胚于二维欧氏平面的一个开球，等价的说法为，每点有一“局部坐标系”。这一例子的另一更重要的特殊性质在于，群运算（可视为恰当的欧氏空间上的函数）不但连续而且解析。这是显而易见的。若上述矩阵用有序对（x，y）等同，则

(u，v)(x，y)=(ux，uy+v)，

并且

(x，y)^-1=(1/x，-y/x)

如果一个群是局部欧几里得的，即可以“坐标化”，则存在许多方法使之坐标化；如果至少有一种方法使得群运算解析，则这个群称为“李群”。希尔伯特的第5问题是：每一局部欧几里得群是一李群吗？

在发现哈尔测度后，冯 · 诺伊曼（1933）迅速用它回答了紧群情况的希尔伯特问题，回答是肯定的。1952年格利森（A. M. Gleason）等人彻底解决了这一问题，回答是肯定的。

参考文献：EDM406/N。

进展5：单群

每一群都有两个显然的正规子群，即群本身和另一极端的由单位元构成的子群。一个群如果只有正规子群，则称它是简单的。

单群在两种方式上很像素数：它们没有正常的部分，每一有限群都可以用它们建构出来。考虑任意一有限群，看它的最大正规子群。如果群是简单的，则最大正规子群就是单位群，但无论如何，不管子群是什么，它的最大性蕴涵，除以它得到的商群是简单的，群、正规子群和商群的关系可以这样描述：原来的群是商群通过子群的一种扩张。用这种语言，每一有限群（除了平凡群（单位群）外）都是单群通过一严格低阶群的一种扩张。这个命题是数论的群论对应物（每一正整数（除1外）都是一个素数通过一个严格较小的正整数的积。）。

如果最大正规子群是不平凡的，则上述过程还可使用；结果为最大正规子群的一个最大正规子群，使得原来的群是第二个商群通过第二个子群的一种扩张。这个程序可以一直进行下去，直到产生出平凡子群；最后得到一递减链条（一种复合系列）。有限群的许多问题都以这种方式归结为确定所有有限单群的问题。

有限单群中的阿贝尔群较容易确定，课堂练习就可证明它们不过是素数级的循环群。这是本领域唯一容易的部分。困难的是找到所有非阿贝尔单群。单群中的某些例子并不难获得；例如在置换群中，最著名的是6阶或6阶以上的交错群。长期以来，已知的单群并不展示任何模式，甚至有关的最简单的问题也未能攻破。例如伯恩赛德（W. Burnside）1911年猜测，每—有限非阿贝尔群都是偶数阶的，这个猜想50多年没有解决。

1963年费特（W. Feit）和汤普森（J. G. Thompson）证明伯恩赛德猜想是正确的。证明占用了《太平洋杂志》一整本：250页。在这之后别人给出了某种简化，但没有发现更短的、更简易的证明。这一结果有许多推论，该方法已被用于攻破有限群论中的许多其它问题；原来一度死亡的领域又重新充满了生机。例如，伯恩赛德的梦想迄今已完全实现了：通过全球许多数学家的通力合作，所有单群都已被找到并能显式地描述。

参考文献：EDM160/D。

进展6：阿蒂亚 - 辛格指标定理

有穷维向量空间上一线性变换是如何丧失可逆性的？有两种显然的回答：它不是单射的（一对一的），或者也不是满射的（映上的）。第一种情况使得存在非平凡核，第二种使得存在非平凡余核。一变换T的核是零化空间，0的逆像；余核粗略地说是值域的补，或者准确地说是整个空间以值域取模的商。由初等线性代数事实可知，两种丧失总是同时发生的，两种丧失的数值测度，即核与余核的维数，总是相等的。

对于无穷维空间，情况有所不同。例如，如果T是无穷维序列空间l²上的单侧移位，变换定义为

T{ξ₁，ξ₂，ξ₃，…}={0，ξ₁，ξ₂，ξ₃，…}，

则ker T是平凡子空间｛0｝，但ran T是所有向量的子空间，其第一坐标为0，因而dim ker T =0并且dim coker T =1。

线性变换T（包括刚才描述的变换）的指标（index）定义为

index T =dim ker T－dim coker T ，

只要它有意义，即只要它不是∞ - ∞。有穷维空间上的线性变换的指标总为0，但对于无穷维空间，指标可以给出有趣的信息，这时指标测度了一个变换不可弥补的不可逆的程度。

阿蒂亚 - 辛格指标定理不得不对付这样定义的“解析”指标。我们中多数人首先撞见的是计算旋转数的柯西积分公式，另一个例子是黎曼 - 罗赫定理，紧黎曼面（如球面和环面）来自复函数理论，黎曼 - 罗赫定理是关于此黎曼面上亚纯函数的某种向量空间的维数的；它的结论是有关维数的一个公式。一般的阿蒂亚 - 辛格定理是黎曼 - 罗赫定理的一种推广。它处理了比黎曼面更一般的光滑紧流形。作用在定义于此流形上的光滑函数的椭圆微分算子有两个数与它们有关。其一为上面提到的解析指标，另一个为拓扑指标。拓扑指标与K理论有关，特别地在经典内容中与欧拉示性指标有关。阿蒂亚 - 辛格定理（1963）的成就在于指出，这两个指标具有相同的值，换句话说，用纯解析定义的解析性质事实上几乎完全可以用基础流形的拓扑性质确定。

刚才提到的方程只是阿蒂亚与辛格联合工作的一小部分。他们的工作的结果最深刻、最普遍，对我这个报告人来说，也是本报告最艰难的部分；它们不仅是一个定理，而且还是一种理论、一种思想，它进入、影响了数学的许多部分，也被数学的许多部分所影响。奥斯曼（R. Osserman）15年前在写微分几何研究方面的重大成就时，称阿蒂亚 - 辛格定理为“分析、拓扑和几何的一项伟大的综合，特别地它引向审视高斯 - 博内定理的一种新途径；它不是一项孤立的结果，而是事情的一项大的方案的实例。”这项综合可能是阿蒂亚在英国被封为爵士、辛格被授予总统奖章的一个主要因素。

参考文献：EDM236/H。

进展7：傅里叶级数

不幸的是傅里叶级数发现时并没考虑收敛性。傅氏级数是经典与现代分析的至关重要的一部分。它们源自拓扑群和算子论；它们也起源于振动弦与热传导问题。

在最经典的表现形式中，傅里叶级数必须处理区间［0，2π］上可积、周期为2π的线上的复值函数。这种函数的傅里叶级数是指数函数e^inx，n=0，±1，+2，…的无穷线性组合，系数通过积分给定的函数来确定。

三角多项式（实的或复数的）是人们熟悉的东西，也是可计算的；的确，把复杂函数表示成此类多项式的极限只有好处没有坏处。因此很自然希望与函数f有关的傅里叶级数的“和”要“等于”f，并且无论如何要寻找哪些函数可以做到这一点。希望的答案是，好的函数应有好的级数，这一领域的发展史很强地受这一期望的影响。

当开始理解了极限时，“和”与“相等”被用逐点收敛来解释；后来有了弱收敛和相对某一范数收敛这样的更富有成效、更有用的概念。

一个函数怎样才算好？可微性足够好，但连续性还不够；存在其傅里叶级数在一点上发散的连续函数（P. D. G. 杜 · 布瓦 - 雷蒙，1876），事实上在许多点上发散。一连续函数的傅里叶级数必然几乎处处收敛吗？这是个多年来未解决的问题。

1913年俄国数学家N · N · 卢津提出如下猜想：区间［0，2π］上平方可积函数的傅里叶级数，在［0，2π］上几乎处处收敛。在长达53年中这个猜想不能证实也不能否定。1923年卢津的大弟子A · N · 柯尔莫哥洛夫构造了一个可积函数，它的傅里叶级数几乎处处'发散。1926年他又发现了一个傅里叶级数处处发散的可积函数。但这两个可积函数都不是平方可积的，因而卢津猜想不能否定。1966年瑞典数学家卡尔森（L. Carleson）利用哈代 - 李特尔伍德极大函数和考尔德伦的原理，以极其精巧的数学论证，证实了卢津猜想。

参考文献：EDM167/H。

进展8：丢番图方程

希尔伯特第10问题是关于丢番图方程可解性的。问题是设计一种算法，即一种可计算的程序，来确定对、于任意给定的（正）整数系数的多项式方程是否有（正）整数解。

说存在一个制定可解性的算法，意指什么？回答这个问题的一种合理的方法是给集合和函数的可计算性下一定义，然后用可计算性这个术语来定义算法。可计算性概念受到广泛注意，有许多不同的定义，但都是逻辑上等价的，也都符合这个词所暗示的直观上的含义。

设｛E₁，E₂，E₃，…｝是要考察的所有多项式中的有效可枚举集，并令S是指标k集（E_k 有一解）。希尔伯特问题可表述为，S是否为一可计算集，回答是否定的。通过J · 鲁宾孙（1952）、戴维斯（M. Davis）（1953）、普特南（H. Putnan）（1961）、马梯加塞维奇（Y. Matijasevi?）（1970）的长期努力，问题才告解决。

证明中的中心概念是丢番图集，证明的主要步骤是每一可计算集是丢番图的，天才般地使用了诸如中国剩余定理、斐波那契数论等初等数论的技术。

参考文献：EDM100。

进展9：巴拿赫基

在微积分（始于17世纪）中我们知道如何求数值函数的极大值和极小值，这些函数的定义域为直线上的区间和平面上的矩形；在稍后的变分计算（始于18世纪）中我们也设法找到数值函数的极大、极小值，它们的定义域为函数集。此类问题都属于泛函分析，在这种分析中函数的定义域为函数集、函数空间的子集，在其中代数方法和拓扑方法都可以大量运用。

看待泛函分析的另一视角为，它是线性代数的一种无穷维推广。第一个思想为用函数和积分（涉及核的应用）代替向量和加法（涉及矩阵的应用）。这一领域的首次系统化工作在20年代分别由巴拿赫和维纳独立地提出，结果便是巴拿赫空间理论及其迅速发展。巴拿赫空间研究是数学中使用公理化方法的典型例子，本身抽象而一般，但根源则具体而特殊。

关于巴拿赫空间的最早的一个问题是基问题，由巴拿赫1932年在他的书中提出。巴拿赫空间的一个元素序列是该空间的绍德尔基，如果每个向量都能表示成该序列的项的收敛的无穷线性组合。定义中“序列”一词的可数性蕴涵，如果巴拿赫空间有一基，那么它是可分的（即有一可数稠集）。持续了40年的基问题是一个逆问题：每一可分巴拿赫空间有一基吗？

研究巴拿赫空间的一个经典上很重要的概念是紧（完全连续）算子，即具有单位球的像的闭包是紧致的这一性质的巴拿赫空间之间的一种线性变换。简单的紧算子是有穷秩算子；另一最简单的是有穷秩算子的（一致）极限，如果一个巴拿赫空间是“好的”，则映射到它上的每一紧算子都是这样一种极限，用技术语言讲，空间有逼近性质。特别地，如果一个巴拿赫空间有一基，则它有逼近性质。

基问题1973年由恩夫洛（P. Enflo）解决，解是否定的：存在可分巴拿赫空间并不具有逼近性质。他采用了构造性技术。

参考文献：EDM39/A。

进展10：流形

2维流形是一拓扑空间，局部上很像2维欧氏空间（即每一点有一邻域，同胚于平面上一开盘），具有这样的性质：它是由许多欧几里得空间小块连续地粘连在一起的，并且粘连的小块个数不太多（即整个空间是可分的）。3维、4维、5维流形可以类似地定义。

—个2维流形可以很大（例如它可以是整个空间），即使它看起来不大，它却可以是内在地大的，在其中许多路径可以收敛到其中并不存在的点——类似于一开盘。研究较多的是紧流形。

所有紧2维流形可以列出来吗？不错。最容易办到的是可定向流形。一类为单连通的（球），另一类有亏格1（环面），再一类有亏格2（有两个洞的炸面饼圈），等等。所有可定向的2维流形都与这些相似（在同胚的意义上）。紧2维流形的分类问题是经典的，很早以前就解决了。一维的情形很简单，可留为作业。

高维流形既难观察又难分类。令人吃惊的是，当维数为5或大于5时，许多答案已找到了！简单连通的5维流形已被理解，可用同伦理论分类，但3维流形的问题没有解决，庞加莱的著名假设与此有关。4维流形有所不同。1982年M · 弗里德曼和S · 唐纳森取得了两大胜利，为此获1986年菲尔兹奖。

每一定向的4：维流形与一行列式为±1的对称盩数矩阵有关，弗里德曼证明所有这类矩阵确实存在。在半时间上矩阵与流形是一一对应的，在其余时间矩阵与流形是二对一对应的。如果我们把一个篮球看作—个2维物体，弗里德曼的工作则为我们指出了4维篮球的许多性质。

唐纳森另一方面证明，如果一简单连通的定向的4维流形有一光滑的微分结构，并且它的矩阵是正定的，则矩阵必须等价于单位矩阵，这是一个很强的结论；它显示，拓扑4维流形理论与可微4维流形理论是根本不同的。

J · 米尔诺在表述弗里德曼的工作时说，结论的证明是极其困难的，M · 阿蒂亚在表述唐纳森的工作时说，它开启了一整个领域，唐纳森的年轻及数学才能“暗示数学并没有失去统一性或者生命力”。

参考文献：MI 5/3/39。

进展11：比伯巴赫猜想

有些问题有趣并不仅仅因为它们有趣，而是因为它们难以捉摸，费马问题可能就是最好的一例。没有人仅仅想知道答案是什么，数学家想知道为什么他们不知道答案。比伯巴赫猜想是关于单叶函数的，对于专家来说它是完全自然的，但对于多数局外人来说，它似乎像一种奇怪的技术。

它所涉及的是由形式

给出的幂级数的所有函数类，函数在开单位圆盘上是单叶的（意味着解析的、单射的，用更经典的词叫单叶的（univalent））。函数类构成一个“正规族”（一种紧致性质），这意味着对于每一n，系数a_n在整个类上有界。比伯巴赫1916年研究这一问题时证明，对于类中的每一函数事实上有|a₂|≤2。这一类中的一个特殊函数，由a_n=n定义的克贝（Koebe）极值函数，显示上界2是最好的。更一般地，比伯巴赫猜想对于所有n有|a_n|≤n。

勒夫纳（L?wner）1923年证明，当?=3时猜想为真；1955年P. R. 加拉贝迪安和M. M. 席费尔证明，n=4时猜想正确；1968年佩德森（Pedersen）和小沢满证明了n=6的情况；1972年加拉贝迪安、佩德森和席费尔证明了n=5的情形；1973年小沢满和洼田佳尚证明了n=8的情形。进展缓慢，前途渺茫。

把猜想变成定理的突破始于1984年，布朗基（L. de Branges）给出一般情形的证明，证明有几百页之多，根据的是他的平方可和幂级数理论。他的原始证明包括一点小毛病，但它们是可纠正的并且不久后就被纠正了。专家们还是有些不安，但他们的不满并没持续多久。他们不喜欢的是，证明竟依靠了似乎不相干的泛函分析的方法。最终，在列宁格勒举行的一次几何函数论讨论会上有人提出一个证明，也许能让比伯巴赫满意。证明篇幅较短，表达也十分清楚，比前人证明n=5和?=6情形时的证明都好。平方可和幂级数这一套是过去了，但布朗基的主要洞见仍然有意义，我们不能洋洋自得而把它们丢掉。

参考文献：MI 8/1/40。

尾 声

本文题目所提出的问题的答案，现在已很清楚了，数学的进展根本没有减慢。