混沌边缘的量子物理学

发布时间：88年10月26日

Michael Berry 编译罗祖德韩王荣

量子物理学描述极小的世界，经典牛顿物理学描述较大规模的世界，然而，在两者之间的边缘地带，却很难找到严密的数学描述，于是，浑沌出现了……

1900年之前，物理学的基础是牛顿力学，其基本原理是力能改变物体的运动方向，这些定律能用简单的数学进行描述。我们会很自然地以为，由于这些定律简单，因此，物体的运动一定也简单。经典力学在说明月球和行星运动规律方面的惊人成功更助长了这一观点，同时，也鼓舞人们去模仿这些规律来发明各种机械，如钟表机构等。

然而，这一观点却是错误的。简单决定论的定律可能产生非常复杂的、甚至随机的运动，因为有些系统相当不稳定，以致其运动过程灵敏地依赖于初始状态，甚至一个台球的运动——原始的牛顿系统——在某些简单系统中也能变得相当复杂。我们能把台球在其运动范围的边界上理想化成一个弹性反射点，换言之，即毫无任何能量损失。

如今，经典力学的“混沌学”是一个相当活跃的研究领域或研究课题——混沌学是两世纪前用于神学研究的术语，当时的意义是研究创世纪前存在着什么东西。它的应用范围自土星卫星Hyperion的不规则滚动一直到液体中食物颗粒的复杂运动轨道。

1920年代以来，我们已知道，牛顿力学只是量子力学所指述的物理学更深层真理的近似，而混沌则不是。当涉及在原子以及更小尺度上的物体和过程时，与实验一致的便是量子理论而非经典理论。最熟悉的形式便是：量子力学是一种波理论。它的一个结论是：一个孤立原子系统的能量不能像经典物理中一样取任何数值，它规定了一系列可能的能级。普通的类比是一根吉他上的弦，在它上面，波具有一组分立的频率或和声，它们取决于弦的长度、强度和密度。最低的能量为基态，系统往往滞留于此；高一点的能量为激发态，适当频率的光照在原子上，就会使它进入激发态。

量子物理学具有其自身的随机性，这同牛顿轨迹所具有的不规则性是极不相同的，例如，我们无法预言—个放射性原子核何时衰变，或者一束激光中下一个质子将在何处碰撞屏幕。但是，由量子力学方程，我们却能从量子波的强度中计算出发生这些事件精度较高的可能性。因此，量子随机性并不在波中，而是在波所描述的过程中。

在日常世界里，量子力学的直接效应小得无可觉察，那是因为量子波的波长是如此之小，甚至对一个截面仅千分之一毫米、一小时仅蠕动一毫米的细菌来说，它的波长也比它自身要小一百万倍——比一个原子要小一百倍。我们知道，比原子大的尺度上，牛顿力学相当有效，因此，量子力学必须得出相同的预言，尽管它们具有非常不同的概念基础。

量子物理学先驱之一的尼尔斯 · 玻尔深知牛顿力学与量子力学间的这一关系，他称之为“互补原理”。当量子力学用于大或重的系统时，它必须与牛顿力学相—致，——这时我们可以忽略波效应，是“经典的极限”。我们很熟悉光学中所使用的原理。光是一种波，但是，在说明照相机和望远镜的工作原理时，把光想象为一组严格定义的线是很有用的，它们很像是牛顿想象的构成光的粒子的轨迹。我们知道，牛顿物理学会产生出混沌行为，根据互补原理，量子物理学在经典极限下与牛顿物理学相当，量子系统如何来反映这一事实呢？在发展过程中，其能级分布的方式有什么特性，从而表现出牛顿轨迹的不规则性的？量子系统能否像它们逼近经典极限那样成为混沌的吗？这些都是量子混沌学的问题，它是一门刚刚崛起的学科，使人们发现了在微观系统中鲜为人知的行为方式。

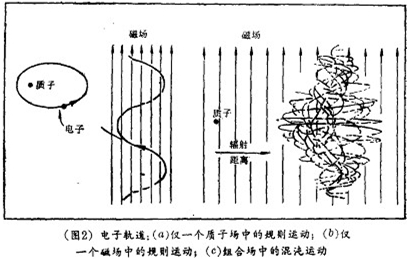
早在十年前，在一项由意大利 - 苏联 - 美国合作的理论研究中，人们就感到惊奇不已，该小组是由米兰的亩罗 · 卡沙蒂（Giulio Casati）、诺沃西比尔斯克的玻利斯 · 奇里科夫（Boris Chirikov）和弗利克斯 · 伊泽拉莱夫（Felix Izraelev）以及亚特兰大的约瑟夫 · 福特（Joseph Ford）组成的。他们研究了高激发态原子中的电子即电子处在极高能态的原子是如何吸收照在它们上面的辐射能量的。为了避免包含许多电子的真实原子必然会遇到的繁琐的计算，他们想了一个简单的理想模型：运动的电子如同圆环线上的小球，无休止地绕着其轨道旋转（图1）。照在电子上的辐射波产生一个振荡力，研究人员将它代表连续的推动，即对“小球”的一连串踢。推动的强度取决于圆圈中小球的位置。

当我们把这一“踢转器”的轨道视作一牛顿系统时，它可能是规则的或是混沌的，这取决于推动的强度：强度太混沌程度高。经典规律性是一种稳定的状态，平均而言，旋转器吸收多少能量也放出多少。当我们把球变轻，以致不得不考虑其波长时，在这种量子的“实验”表演中，还是能发现这性质；另一方面，经典的混沌对应着不规则的扩散，平均地讲，旋转器是以恒定的速率继续吸收着能量。

然而，在混沌状态中，相应量子旋转器的表现则不相同。开始，旋转器的能量沿着经典的直线上升，但到最后，在某一“转折点”，能量开始很慢地增长，甚至可能减少，这是件意外之事！量子力学阻碍经典混沌，初看上去，这似乎是对互补原理的冲突；但是，当我们改变量子模型使它更经典些，例如使粒子更重些，那么，标志着非经典效应开始的转折点则变得越来越迟。理论家们是用计算机以数值来解量子方程时发现了阻碍混沌这一现象。研究了十年之后，人们弄清了，这种阻碍是微妙、灵敏的波互相干涉效应，但是，物理学家尚未完全解决这一问题。

真实原子不同于模拟旋转器，它里面的电子能被激发得完全脱离原子核——这从而导致发生电离的可能性将取决于辐射强度以及该原子开始时是如何被激发的。这些条件决定了经典电子轨道是混沌的还是规则的，以及利用经典近似方法计算的电离几率是否与用更精确的量子力学定律所计算的相同。

物理学家用微波照射氢原子进行了实验，在经典的混沌条件下，经典的和量子的预言相一致——即在转折点之前。他们惊奇地发现，和原子一样小的系统竟呈现出经典性质！须知原子吸收、放射光子是一个高度非经典的过程，光谱中发射线和吸收线的图形是发现量子力学的可视现象之一。

新光谱学与旧光谱学之间的不同之处在于，新实验使用强辐射，原子一开始就处于高激发态，因此，它们大量地吸收、放射光子，而并非一、两个光子，理论预言，对旋转器来说，量子力学最终将阻碍经典混沌。用实验检验这一重要效应将要求我们计算长期照射后的电离情况，这在技术上是很难的，因此，至今尚无人打算去这么做。现在，我们转回到系统的量子混沌学上来，该系统或被隔离，或施加不变的外力——相对刚才设想的辐射振荡力而言，这种系统的能级描述了它的量子状态，它说明，高激发量子能级的分布——类似音乐中和声音符的图形——基本上取决于相应的经典系统的轨道是规则的还是混沌的。

磁场两极所构成的系统是指氢原子中的一个电子置于极强磁场之中——比如，白矮星上的磁场，它比地球磁场要强百万倍之巨，在低能时，氢原子的核子，即质子，将电子牢牢地束缚住，质子与电子间的静电力完全控制着磁力，经典轨道就如同行星绕着太阳一样为椭圆形，不存在混沌现象（图2）；在极高能时，电子远离原子核，磁力便占了上风，轨道为绕着磁力线的螺旋线，还是不存在混沌现象；然而，在中能时，两种力互不相让，施加着相反的影响，于是，经典电子便以混沌运动来消除矛盾。

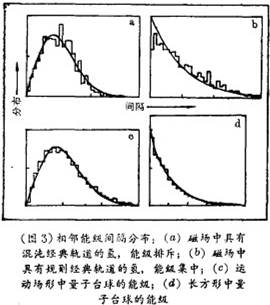
由于电子以量子方式出现，我们不得不在比较规则和混沌的统治下大量激发能级的分布状况。一种方法是计算能级的统计值。一种方便的统计法是在原子的能级光谱中在低能以及中能状况下计算邻近能级间的间隔。如果能级规则排列，类似阶梯，间隔分布将集中于平均间隔，产生如图3 a的曲线。要是你绘制一群人的高度，你也将得到相似的分布。这种情况下，几乎没有小间隔——就仿佛能级互相排斥一般。如果另一方面，能级是随机分布的——即互不相关，就像阵雨中雨点到达的时间——间隔的分布将是无限制的，小间隔居多。人们惊讶地发现：当经典轨道混沌时，能级排列得更规则（图3 a）；而轨道规则时，则是随机分布（图3 b）。有关磁化氢的实验甚至证实了理论上计算出的光谱的微妙细节。

这种行为不仅是磁化氢原子所固有的，相反，量子能级的间隔总是仅取决于经典轨道是混沌的还是规则的，而不取决于系统的其他细节。为了说明问题，图3也绘出了台球游戏的两个量子描述的能级间隔。运动场形游戏是经典的混沌，但其量子能级具有规则间隔（图3 c）；而长方形游戏是经典的规则，但其相应于混沌运动的量子能级具有随机间隔（图3 d）。这些导致了互相排斥的现象。量子台球可能呈现出理论家们远离实际世界的奇异世界，但是，恰恰是同样的数学可用来描述形状类似台球桌的振动薄膜的频率；在三维情形中，它也可用来描述音乐厅的音响效果。

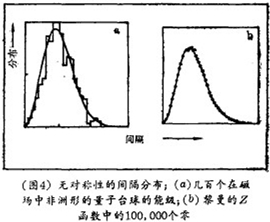
图3 b和3 d中的能级斥力并非经典混沌中最普遍的量子特征，因为迄今为止所讨论的所有系统均具有一种特殊性质，即对称性：磁场中的原子具有圆柱体对称性，台球的运动具有时间的对称性，在这意义上说，如果任意时刻的运动台球速度相反了，它就将回复到原先的轨道上去。当不存在任何形式的对称性，而且经典轨道是混沌的——环境的组合仍在实验范围之外——理论预言：能级间的排斥仍会存在，如图4 a所示，它会变得更强烈些，其中，曲线的斜率在零间隔处消失了——曲线变平了。

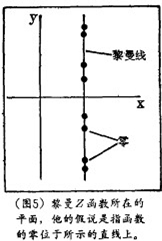
在这一点上，量子混沌学意外地与纯数学中长期存在的难题之一有关了，即黎曼的数论假说。1859年，乔治 · 伯恩哈德 · 黎曼（Georg Bernhard Riemann）——他是个德国数学家，他还发展了包括三维以上几何学的研究——正在研究素数的分布情况，他设计了一种数，称为Z函数，其数值依赖于复平面上的位置，复数（由S表示）具有“实”部以及含有-1的平方根的“虚”部；x轴代表实数，y轴代表虚数，黎曼函数扩展到整个S平面：

Z（S）=1+1S/2+1S/3+…

他著名的假说是：Z函数为零的那些点都位于x=1/2这条直线上（如果该假说为真，某些关于素数的定理就将成立）。数值研究显示最初的15，000，000个零都在黎曼线上，但尚无人能证明所有的零都在其上。

与量子混沌学的结合是由安德路 · 奥德列斯库在对邻近零之间的间隔分布的计算中得出的、这项计算花费了Cray超级计算机约20个小时，结果便是图4中的曲线。这还不是图4 a与4 b间明显的相似性，但也是其他证据的一种变换，即认为基本的黎曼Z函数是一些未知的经典的、力学的系统，其轨道是混沌的、无对称性的，它的特性是，当量子化时，其能量即为黎曼零。这些量子力学中表面上无法比较的世界与数论之间的结合是很鼓舞人心的。