“纯”数学和“应用”数学
作为现代的日常用语,“基础科学”和“应用科学”两词经常为人们所使用。通常,它们的含义如下,即:目的在于理解某种现象的是“基础科学”,撇开好坏不谈,当人们以控制某种现象为目标,以期对自身有用时,则为“应用科学”。虽然有的人担心“应用科学”有时会引起灾害,但是却很少有人怀疑“基础科学”——姑且不谈有何用处——的价值。
在数学方面,通常不说“基础数学”,而以“纯数学”和“应用数学”两相对比。事实上,稍加分析这两个名称所表示的含义,就可以看出这两者在心理的作用方式上大相径庭,倒不如分别称为“数学”和“数学应用”为宜。
那么,数学的“应用”究竟是什么?我可以这样说,那就是:在给定的条件下,根据普遍法则来预见可能世界的对象将会如何变化,制成想要研究某种状况的数学模型。就是说,所研究的事物“表现”为对应的数学对象,使对应的数学对象之间的“关系”符合这些事物所遵循的法则,把原先的问题翻译成数学问题。如果能找出这个问题的完全解或近似解,再反译回去,那么所给的问题就得到了“解决”。
当代广为人知的例子之一是人造卫星或火箭的制导。它用伴有对应于重量的系数(即一个数)的空间内某一点来表示,其位置用有关某一固定坐标轴的三个数来表示。进行观测的时间可以用时钟来计算(又一个数)。发射的火箭受到地球、月球、太阳,有时还有其他行星重力的影响。在模型中,这些力用矢量表示,它们的各个成分规定为火箭坐标的函数。要确定其运动,按数学模型把运动力学定律译成常微分方程来求解。
使数学模型对应于力学定律和天体运动定律(所谓“天体力学”)并出色地符合观测结果,这是17世纪到18世纪数学的一大成果,其实,这些模型确实是硕果累累的数学应用最早的例子。因此所运用的诸定理属于微积分的“初级”部分,在当时却是人们交口称赞的对象。如今已失去往日新颖的光辉,成为高中到大学低年级的课程。
理论物理学和数学
从19世纪到20世纪,数学愈来愈广泛地应用于物理学,其性质也发生了变化。与上述天体力学的情况相比,人们在试图为流体力学、弹性体力学、电磁力学或热力学,以及后来的相对论,量子论等种种新理论制作数学模型时所遇到的数学问题,特别是有关偏微分方程的问题要棘手得多。其中最简单的例子有“弦振”方程式:
?2u/?t2-C2(?2u/?x2)=0
以上、x表示弦的位置,t表示时间,u(x,t)表示x位置上某一点在t时间移动的长度。
虽然在这些模型中,也有一些是早在18世纪就已提供的,但是由此产生的问题却非当时的数学家所能胜任。为了求得对于物理学家来说有意义且有效的解法,19世纪的微积分专家们必需竭尽全力。许多问题至今还只有部分解答,所以人们在不断探索更新的研究课题,更新的突破方法。
为满足物理学家的要求,称为“泛函分析”的新学科就这样应运而生。作为更新的事例,是概率论应用于统计学、物理学中产生了概率论方面的许多研究课题;同样,还有从奥佩莱欣茨 · 利萨奇、奥托马顿的理论受到鼓舞而发展起来的代数学领域。
古典时代数学的应用
牛顿力学及其在天文学上应用的惊人成功,特别是克莱罗以不超过1个月的误差预测了哈雷彗星的复归,给了欧洲的知识界以非常强烈的印象。其中也有例如伏尔泰那样对数学一窍不通的文士②。由于取得了这些令人瞩目的成就,克莱罗、达兰贝尔、拉普拉斯等数学家便认为:数学研究最根本的目的在于给力学、物理学提供模型。因而凡不能满足此条件的数学分科全都无用。
17世纪以前的数学应用绝不是像在牛顿力学中那样深受世人赞叹的、几乎带有魔术性的事业。事实上,由数学家创造出给自然现象以合理“解释”的模型,只有以下四例;它们都出自希腊数学事之手;在那之后直到16世纪以前没有出现过一种新的思想。这四个例子就是镜面光学(“反射光学”)、静力学、浮游物体的平衡状态(这些都是在公元前四世纪以后)以及天文学(公元前6世纪已经可以看到最早的成果)。
这些应用都仅仅局限于几何学,都表现为几何学的附属。为了记述某种运动,原有的数学工具是不够的。因此它必须通过无限小分析来记述。希腊人认为:要“解释”天球上行星的运动,只有围绕某一根轴(如果在平面上则围绕某一点)的匀速旋转才能在先验上得到允许。这或许是因为当时还残存着关于星球的“神性”的神学观点,相信星球具有卓越的“完美性”所致。这里介绍一下希腊人在天体观测方面,用迥异于其他古代文明的构想方法取得的最初成果的概要。
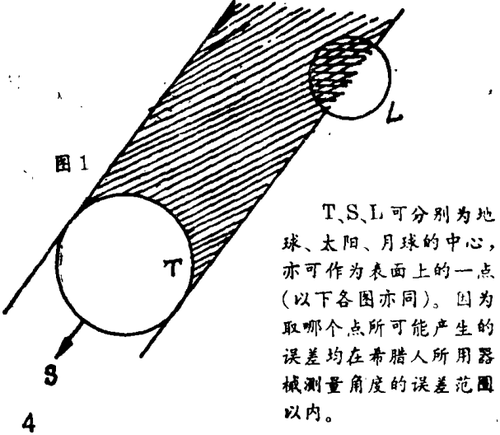
最早的一步是由6世纪的毕达哥拉斯学派首先迈出的。他们坚信地球、月球、太阳都是完整的球成,认为月亮的盈亏是由于月球和太阳在围绕静止不动的地球旋转时,阳光所照射的部分发生变化所致,月蚀是由于月球进入了地球阴影的锥体部分(图1),为了解释此时地球的影子在月面上呈圆弧状(图2),他们只有假定地球是圆的。
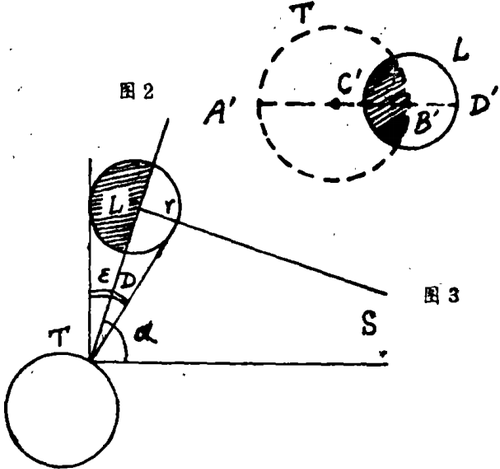
根据其他的观测,他们还了解到TS比TL大得多,实际上,分开月球明亮部分与阴影部分的平面通过T,直线TL垂直于LS(图3)。因此
TL/T=cosα
其中,角α接近90°(误差在1分以下),TL/TS之比大体为0.003左右。由于很难面向太阳测定角度,希腊人假定α大致为37度,所以他们所得的TS值过小。
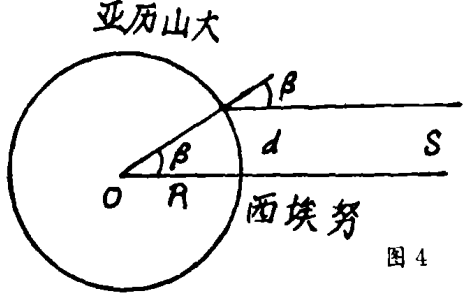
即使假定由太阳射到地球上各点的光线全都平行,那也不会发生很大误差。公元前300年,埃拉托斯泰内斯这样来求地球半径的近似值:埃及的亚历山大港和西埃努(今阿斯旺)大体在同一子午线上(图4)。夏至日,正午的太阳位于西埃努的正上方。设同一时间太阳光线与在亚历山大的垂直线的夹角为β,由于它同时也是连接地球中心O与亚历山大和西埃努的两条半径之间的夹角,所以连接这两个城市的圆弧长d=Rβ(但β以弧度计算)。因此R=d/β,埃拉托斯泰内斯已经知道d的大略值。
根据这个R值,用图2所示地球与月球直径之比A'B',C'D'可求出地球到月球的距离TL。由地球落在月球表面的阴影的圆弧曲率,已知该比值大致为3(实际为3.7)。如果测量观察月球的角度ε,设月球半径为r,则D=2r/s(图3)。
包括牛顿及其18世纪的后继人所建立的天体力学在内,这里所说的数学应用都属于“基础”科学。应当注意的是:在研制人造卫星之前,天体力学与实际应用完全风马牛不相及。尽管如此,公众对这门科学的赞赏,却成了自希腊以来一直延续不断的传统之一;而希腊人,借用亚里士多德的话说,总是把“与追求用途和利润无关的科学”视为有价值的东西。这正是人类的一种特性,它与幼儿们已经明显表现出来的好奇心有关;尽管许多成年人由于陷入了碌碌无为和萎靡不振之中,行来似乎已经失去了这种好奇心。
来自功利主义者的攻击
对于达兰贝尔来说,数学家唯一的目标只能是应用于其他科学。但是在他的身边,就像布丰,特别是狄益罗那样,有些人甚至比他更强烈地表现了对数学的反感。对于狄德罗来说,数学的作用业已告终,数学已经不再对经验有任何贡献可言;它无助于“哲学的大众化”,而只是“挡在自然与人类之间的一块幕布”。虽然与伏尔泰不同,狄德罗具有数学的素养,但是肯定他早就意识到不能靠数学来从事独创性的工作。他对数学的攻击就是因为这一点吗?早在1699年,冯特涅就已写道:“人们把超出理解的事物称为‘无用’,这只是一种报复。大体说来,数学、物理学都不被理解,所以才蒙上了‘无用’之名。”
不能不承认:也到20世纪初期之前,力学也好,理论物理学也好,对“实用的”技术发明都没有丝毫影响,虽然这等于在为狄德罗及后来仿效他而攻击数学的人辩护。“简单的器械”(杠杆、滑轮、螺钉等)古已有之;蒸气机在热力学创立以前业已问世;爆发式发动机和飞机都不是由理论,而是由“手工艺”产生的。“基础科学”所造成的结果,以致数学直到今天才为工业技术所必需。认为能够把数学家的工作仅仅限定为狄德罗所指的“大众比”活动的革命家们,觉察到自己的错误,不得不赶紧收回自己的论点。
流行的独断
蔑视“无用”数学的人们,大概也不得不承认:在如今形成的浩瀚的数学知识中,有相当大一部分不可能今天马上就付诸“应用”。尽管如此,他们仍反驳说:这部分按理将来也会“有用”。但是这类说法涉及的是不肯定的未来,所以是既不能驳倒、又不能证明的独断。他们的论据之一是:早在1300年前,阿波罗尼乌斯就不抱任何“应用”目的创立了圆锥曲线理论,开普勒从这个理论中发现了太阳系行星运动的模型。还可以举出最近的两个例子:相对论的模型存在于60年前的黎曼几何学中;群论和希尔伯特空间理论对原子乃至“基本粒子”的结构发挥了重要的作用。
可是,有以下三个值得注意的数论定理:
Ⅰ(欧几里得,公元前300年):存在转无限多的质数(按欧几里得的说法,任何质数都小于某个质数)。
Ⅱ(拉格朗日,1770年):任何自然数都能表示为1、2、3或4个自然数的平方和(例如7=22十12+12+12)。
Ⅲ(维诺格拉多夫,1937年):存在着某个(非常大的)自然数N,大于N的奇数要么是质数,要么等于3个奇质数之和*。
以上结果的性质都是只有无限多的数。如果加以限制,例如限定为101000以下的自然数,定理仍可成立。但是对于几乎所有的数学家来说,那已经不那么引人入目了;而在物理学理论中,考察无限多的整数集合的情况是难以想象的。
此外还有令数学家惊愕的意见。那就是科学史家的如下观点:数学史著作仅仅停留于记述过去的思想以及阐明它们的联系和相互影响是不够的,还必须“说明”数学家为什么选择了这样那样的研究方向,又是如何取得成果的。也就是说,无论是数学还是其他学科,大概都从来没有理性地“说明”过创造性头脑的活动方式。所了解的是:来获成果时的摸索时期会延续很久,然后突然“眼前一亮”,接着就把受到的启示加以整理、总结。彭加勒根据自己的体验,详细叙述了这一过程中的情况。
谈到数学家要解决的问题的原由,可以说,这始终是通过阅读古典著作和教科书、对话、通信或听讲演这些方式与其他数学家交往而产生的。但是对于以批判眼光看待数学家自身形成的数学观的一部分科学史家来说,这是不够的。他们试图断言存在着周围社会环境影响这种万能的“解释”。这是许多知识分子为了将一桩桩贡献和独创性贬低到最小限度、与英雄主义斗争而提出的独断之一。在其他科学中,我没有能力判断这种独断几有何等价值;就我而言,很难理解牛顿、爱因斯坦所生活的社会如何给了他们的发现以影响,但是只要涉及到数学,除去成为其他科学的模型那部分以外,无论是从过去几世纪数学家的研究方法来看,还是从现代数学家的行动来看,这种独断完全没有道理。对于欧几里得来说,普托雷麦奥斯时代的亚历山大;对于拉格朗日来说,路易十五统治下的巴黎或腓特烈二世统治下的柏林;对于维诺格拉多夫来说,斯大林时代的苏联这样一些完全不同的社会环境与上述他们的数论定理之间,究竟有何共通的因素可言?
结 论
上面已经谈了很多,现在简要地概括如下:
(1)数学的重要部分,是为了给其他科学提供模型而产生的,对此不能轻视,但这一部分在现代的全部数学中,不超过30 ~ 40%。
(2)正如哈代所说,促使数学家从事研究的最主要动力是理智上的好奇心、奥秘的魅力和对真理的求知欲。希尔伯特说/问题在那里,所以你就应当加以解决形成动机的还有想给后世留下些什么的愿望,或在世时就使其功绩得到赞扬的雄心,尽管这既非数学所特有。
(3)数学家清楚地意识到:只有从同行那里才能得到这种赞扬和尊敬。他所生活的是一个几乎与外部没有联系的封闭世界,除去成为其他科学模型的部分以外,他遇到的问题也都是在这个世界中产生的。
(4)不管自己对自己的工作怎样高度评价,仍要依靠其他同事的判断来确定其价值。而且,这种工作不会“微不足道”。问题越难,过去以失败告终的尝试越多,对其工作的赞扬就越会层层加码,除此以外,没有什么超越时代或者不因数学家的不同而改变的固定的评价标准。人们在使用着“普遍性”、“高深的”这些词,而它们的含义未必总是相同的。加之,由于一阵阵的时髦或狂热的风气,有时某个分科也会以其他分科为牺牲而吃香一时。这样,评价发生分歧的情况就与艺术作品方面的争论相似,实际上,数学家常常想谈论定理之“美”,这不能不使其他学科的科学家感到惊奇。对于他们来说,唯一的鉴定条件在于理论和公式的“正确性”,即何者能更好地解释观测到的现象。在数学中,一切结果在按照公认的逻辑定律得到证明的意义上才是正确的,未被证明的东西不是数学。因此,要评价数学上的贡献,需要有其他鉴定标准,而这必然是主观的。由于这个缘故,也有人说数学在更大的程度上是一门艺术而不是科学。
[科学(日),1989年第8期]
————————
① 本文原为著者在1987年出版的《为了人类精神的荣誉》(Pour I'honneur de I'esprit humain)—书的第二章。
② 伏尔泰曾在某处写道:他怎么也搞不懂一个角的正弦为何不与该角成正比。——原注
③ 作为这种分解的例子有:33=23+7+3=11+11+11。就所有非质数的奇数而言,这一结果可以预料是成立的。要表明这一点,考察一下N以下的数就行了。但是由于N太大,性能非常高的电子计算机目前也派不上用场。——原注