两位研究一个违反直觉的猜想的数学家,解决了一个50年之久的难题。
大约在二十年前,德国数学家库尔特 · 魏格纳(Kurt Wagner)提出了一个关于图的性质的猜想。这个猜想乍一看来令人难信,甚至连他的研究生也不敢信。然而,这个猜想很吸引人,而且因为它很基本和重要,许多数学家都想证明猜想对还是错。俄亥俄州立大学的内尔 · 罗伯逊(Neil Robertson)是其中的一个研究者。他说,作为一个职业研究员,他对魏格纳猜想研究了整整20年。现在罗伯逊及其同事保罗 · 西摩(Paul Seymour)(西摩最近已搬到新泽西州穆里山的贝尔通信研究所去了)已稍有成功的端倪。他们证明了,魏格纳猜想在许多特殊情况下是对的。为此,他们证明了另一个自三十年代以来数学家们一直没有解决的猜想。美国电话和电报公司贝尔实验室的数学研究主任罗纳德 · 格雷厄姆(Ronald Graham)说,他们的结果是“非常强有力的”。
事情始于1930年,当时波兰数学家凯西密尔 · 库拉托夫斯基(Kasimir Kuratowski)提出这样一个问题,即什么使得某些图——由线连结起来的有限个点的集——不可能在平面上画出来,如果连线之间没有相交的话。数学家们已经知道有许多图不可能在平面上画出来,但是谁也不知道这些图所具有的这些性质的本质。
这不只是个理论问题。例如,电子计算机线路板上的电路实际上就是这样一些图,——线路板上的晶体管可视作“点”,导体可视作“线”。今天的超大规模集成电路设计师们需要知道,是否有一些电路设计方案使得线路板上晶体管之间的导线互不相交。
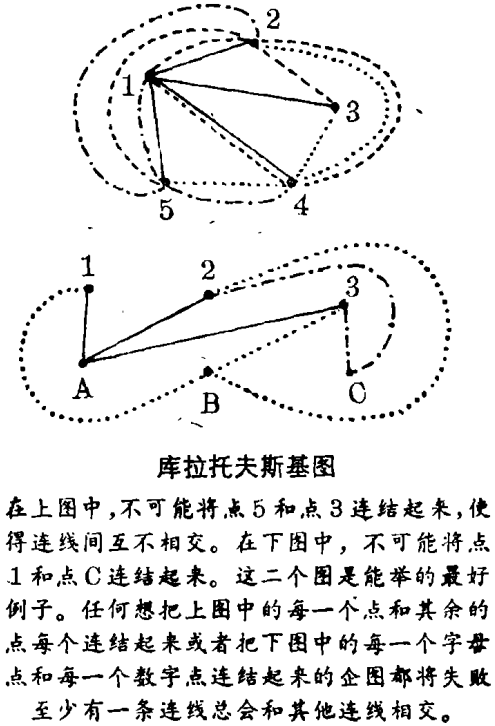
在库拉托夫斯时代,数学家们已经找到了一些不可能在平面上画出来的图的简单例子。其中有二个图最为简单。一个图仅包括标有A,B,C三个点,另一个则是包括1,2,3三个点的集合。不可能将每一个字母点和每一个数字点连结起来,使得所有这些连线都互不相交,——除非离开平面在空间将一些线结成环。另一个例子是有五个点。不可能将五个点中的每一个点和其余的四个点都连结起来,使得所有这些连线都互不相交,或者不离开平面。库拉托夫斯基表明,就是这两个图使问题变得那么困难。数学家们现在把它们称为库拉托夫斯基图。任何图——只要包含有这二个图中的一个——就不可能在平面上画出来;不含有这二个图的任何图都能够在平面上画出来。
以后,在三十年代初期,匈牙利数'学家保罗 · 埃德斯(Paul Erd?s)提出了库拉托夫斯基的结果能否扩充的问题。他问、不可能在其他表面上画出来的最小的图一不含有任何其他的图是怎样的?库拉托夫斯基图能够在较复杂的表面上画出来,表面的典型姑扭曲的或是带手柄状突出部的表面。例如,在一个平面上无法安置妥的线能够通过突出部连接起来。埃德斯知道,这样的例子可能还有,而且更复杂,它们不能在这类表面上放置妥。但是,他不知道,这种图是否无限多,正像质数有无限多一样?
问题远比想象的来得困难。直到1980年,尚无人在此问题上有所进展。此后,俄亥俄州立大学的丹尼尔 · 阿奇德康(Daniel Archdeacon)、亨利 · 格洛弗(Henry Glover)、菲利普 · 休纳克(Philip Huneke)和C. S. 王(C. S. Wang)证明了,对于莫比乌斯带最少有103个图,其中许多图是和库氏图粘在一起的。库氏图本身能够在莫比乌斯带上画出来(所谓莫比乌斯带,就是将一根窄带扭曲后,将其二个头连在一起而形成的带)。接着,俄亥俄州立大学的研究人员们证明了,对于一个有一个突出部的球面,图最少有800个以上。对于有二个突出部的球面,图最少有80,000个。“这似乎是一种无底洞式的问题”,西摩说。当时甚至还不明白,最少量图的数目是有限的,它必定止于某处。
然而,约在一年前,阿奇德康和休纳克在一种表面上一一它们和莫比乌斯带一样是经过扭曲的——找到了图的最少数目。数学家们把这些表面称为“不可定向的”,因为你在上面无法定向而说出在“内面”还是“外面”。就在最近,西摩和争伯逊作为研究魏格纳猜想的一个结果而证明了,对于所有的表面,不论是可定向的还是不可定向的,最少量图的数目都是有限的。
魏格纳猜想实际上包含了埃德斯提出的问题。在六十年代,他提出,对于一个图的任何性质,最少量图的目录是有限的。这些性质包括不可能在平面上画出一个图,使得所有的线都互不相交。罗伯逊说,魏格纳猜想的其他重要的特殊情况是,能够充分相连的性质,这意味着图上的任何二个点可以有许多连结它们的道路,而又互不相交;以及四色不可能的性质,是指不可能用四种颜色中的一种赋予图上的每一个点,而图上没有连结相同颜色的二个点的线。
西摩指出,魏格纳猜想的另一表述方式是说,任何图的数目,若其中没有一个图包含在另一个图中,则必须是有限的。这个猜想似乎是违反直觉的。西摩说:“没有人相信这个猜想”。但是,他和罗伯逊最后还是找到了解决它的方法。他们利用这样的观察:如果他们取一个最少量图的数目,想证明它是有限的,那么,他们就可以取出这目录的一个成员,然后利用这个成员不包含在目录的其他成员中的事实,来说明其余成员。西摩说,“这样就可以对其他成员有所了解,并且给予目录一批结构。”很显然这种方法并不巧。西摩指出,事实上,“指望这种方法很有效,是不明智的。”
但是,一当罗伯逊和西摩发现解决方法,他们就能够证明魏格纳猜想的两种不同变型。首先,他们证明了,对于在其上有有限个凸出部的表面上的任何图的目录,魏格纳猜想是对的。其次,他们证明了,对于至少包含有一个平面图的图的数目,魏格纳猜想是正确的。
西摩和罗伯逊说,这项工作花了两年时间,而且结果已经写成了七篇论文,每篇约有40页长。还有一些论文将要发表。格雷厄姆说,每篇论文都是“严密的”。西摩和罗伯逊仅仅用笔和纸便取得结果。西摩说:“我甚至不知道怎样用电子计算机处理这项工作。”
现在按格雷厄姆的话说,魏格纳的令人惊奇的猜想算是“有点眉目了”。虽然似乎仍然不能列出不可能在特定表面上画出来的所有最少量图的数目,但这数目是有限的这个事实“是一个令人鼓舞的征象。我们或许能用其他方法来表征它们”。这些结果应用到实际问题——如电子计算机线路的设计——尚为时过早。但是,格雷厄姆指出,这些结果至少导致更好地理解可能需要许多层电路的网络。此外,那些科学家对它们是很感兴趣的,他们企图搞清抽象表面的性质,搞清怎样表征能够在这些表面上画出来的图。
[Science,1984年5月4日]