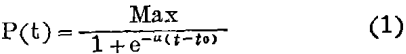导言
诺贝尔奖金授予的最基本的准则是奖给本世纪最杰出的人才。瑞典的诺贝尔基金会每年都要煞费苦心地从全世界搜寻对人类利益作出最卓越成就的贡献者。他们尽量自觉、公正地从事这项工作,并且常常不顾各种政治压力和影响。
另一方面,世界上最优秀的科学家,常常是才华横溢和富于抱负的,他们希望,有时愿意为了争得这一殊誉而进行激烈地竞争。许多研究机构、院校和国家则以获得诺贝尔奖的人数和偶尔问鼎期待已久的诺贝尔奖而引以自豪和衡量自己,正像奥林匹克运动会那样,获奖者被视为凯旋而归的民族英雄。
在我们的研究中,把诺贝尔奖的竞争看作类似达尔文的进化论“优胜劣汰”(逻辑增长)。这项工作受到许多美国当代诺贝尔奖获得者的激励,特别是C. 马采蒂先生,是他首先给我指出了美国诺贝尔奖所处的位置。
美国霸主地位的衰退
竞争中的增长是用一个逻辑函数进行数学描述的:
Max、a、t0是常数。
公式(1)是微分方程的解,该式表明总的竞争增长百分率与增长的剩余数成正比。显然,Max是一个可能达到的最大值,被看作与所有的奖位被获有关。很多论文中大量运用了逻辑增长曲线来研究诺贝尔奖的获奖情况。从后面的参考文献中可以看到一些不同的例子。
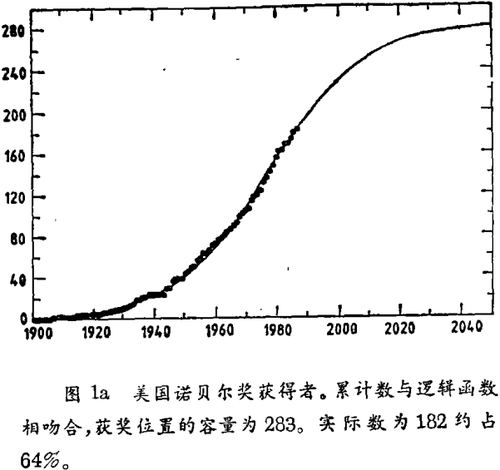
考察美国诺贝尔奖获得者的情况,人们可以根据美国诺贝尔奖获得的累计数,找出逻辑曲线的三个参数。如果我们把所有学科一起考虑,并把每一位获奖者计为1——即使他或她与别人分享诺贝尔奖——我们可以得到如图1a所示的结果。所有的数据是与3参数的逻辑曲线吻合得非常好。截止1987年底,全部奖位的64%已被占据。今天在所有的美国人中有182位榜上有名,曾经283次获得诺贝尔奖。
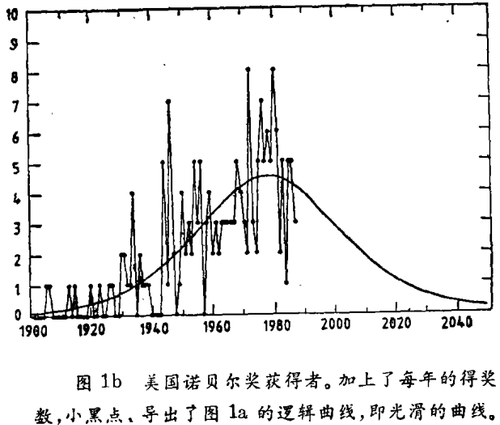
图1b展示了每年的授奖情况。其中那条附加的光滑曲线是根据图1a所决定的函数推导出的。它显示出每年最大的获奖率为4.5个,从1978年后开始下降,1987年为4.0,到2000年预计为2.9,2050年为0.2。显然,这个结论是牵强的,观察每年巨大波动的原始数据的情形可以看出,10年以前这种下降已经开始了。
由此,人们会立即产生这样的问题:“如果美国人获得的诺贝尔奖越来越少,那么谁将获得越来越多?”要回答这个问题,我们必须考虑各竞争者所占有的百分比,并寻找他们之间的替代曲线。事实上,从下面的研究可以看出,美国的下降并不像图1所显示的那样。
世界范围的竞争
这里使用的是一般的逻辑替代函数,假用市场占有率的概念,即在给定的市场内,成功的竞争者进入和占有市场的数量,这是由拿克生努费克提出的。在我们的案例中,市场是每年诺贝尔奖的总数,竞争者包括所有的国家。截止1987年底大约40多个国家分享了总数为662位诺贝尔奖获得者。绝大多数国家仅仅得到为数很少的奖。因此,为了展望未来趋势有必要将各个国家分为几个群体来研究。最成功和最合理的划分方法是将各国分成三个地区。很清楚美国是这样的一个地区;“传统”的欧洲是另一个地区,包括法国、德国、英国、苏联、意大利斯堪的纳维亚国家,比利时、荷兰、奥地利、瑞士、西班牙和爱尔兰。第三个群体是由其余国家所组成的,即所谓“另一世界”。它由许多第三世界国家和发展中国家所组成,但是也包括一些令西方望而生畏的竞争者,诸如日本、澳大利亚和加拿大。
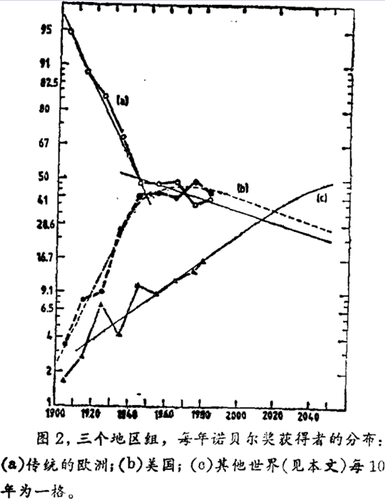
这种分类的形成是很自然的,因为当我们把三个群体的占有率作为时间的函数描述出来,就会发现其具有典型的逻辑函数特征。传统的欧洲占有率已经不断地下降了。直到第二次世界大战美国继续上升,而其他国家开始向前发展。
到第二次世界大战结束时,美国达到了惊人的比率(远远超过其他的逻辑曲线的路径)但是实际上已经达到了顶点。在过去的50年中美国所占的比率并没有增加。“另一世界”在这一时期有了更多的增加。这是以欧洲的减少为代价的。然而,这种替代比战前,美国和欧洲之间的惊人的替代比率要小得多。按变量ln[f/(1-f)]画一条直线(逻辑轨线),这里f是给出的一个群体的分数,得出了一个预测值(细线),如图2。这一结果指出“另一世界”将在2010年超出欧洲,而且2035年超过美国。美国在2000年就开始失去其竞争优势。
这样,尽管美国每年获奖人数已经在下降,而在2000年以后,其竞争力的下降必然会出现。如果这是事实的话,那么将来,诺贝尔奖获得者的总数也会下降。当我们看了第6部分后就对这种未来的现象不会感到惊讶了。
瑞典——俄国人的微量位数
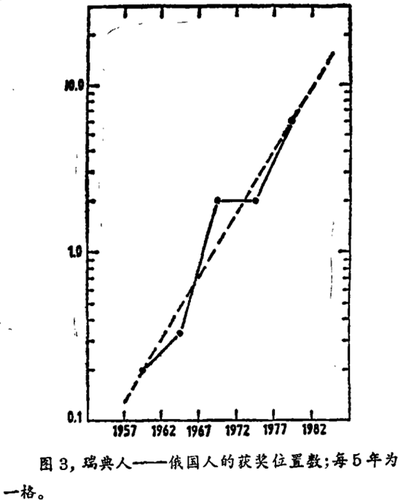
在把有关国家结合起来进行分析的过程中揭示出—些持续存在令人注目的趋势。在1957年1982年间,俄国的占有率急剧下降,而瑞典则骤然上升。其斜率非常相似,这使人们觉得存在着一对一的局部微量位数的替代。
确实,两国获奖总数几乎是一个常数,所有5个5年间隔期间都是5个获诺贝尔奖者,瑞典与俄国的比率的对数与一条直线十分吻合(见图3),即逻辑替代曲线的标志。这能表示出统计的波动吗?这是否会使人们下意识地认为这种现象是由于诺贝尔奖委员会设在瑞典,而这两个国家之间又存在某些敌意的结果?或者可能是一种局部微量位数自然的逻辑替代?
有两种论点引人注目,而这两种都坚持上述第三种假设:其一是把竞争与年龄联系起来。瑞典的获奖者平均年龄为65.1岁,远高于同期苏联人的平均年龄67.5岁。在美国超过欧洲,以及后来的“另一世界”超过美国(见第六部分)的过程中,或许并不存在达尔文式的“优胜劣汰”。第二种观点,就我本人而言,认为缺乏足够的理由来定义瑞典和俄国以外的诺贝尔奖的一个位数的界限,特别是在1957 ~ 1982年这一时期。
无论如何,考虑到在近5年中没有瑞典获奖者,我们可以看到这种现象已经结束了,而这种现象的导火索是1956年俄国对匈牙利的不受欢迎的干涉所引起的。
妇女获奖者
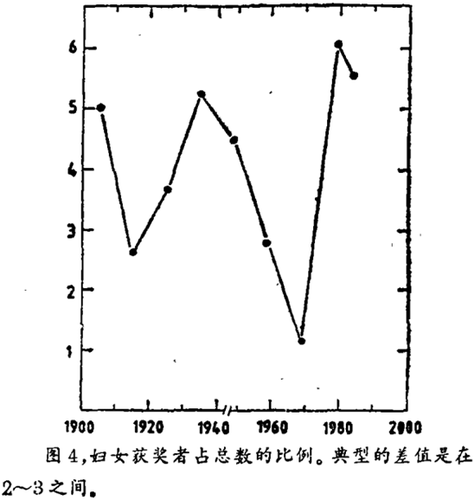
妇女获奖者的百分比总的说来是低的。基本上在3—4%徘徊。但是,从图4上可以看到有一个比较系统的变化。数据的两端误差值在2 ~ 3%之间。呈现出50年左右一个周期,分别在30年代和70年代末80年代初产生峰值。这可能不是一种偶尔的巧合,妇女运动的高峰期也出现在同样的时期。还有,50年的周期性强烈地提示我们这和康捷拉耶夫以及后来的马契蒂提出的55年的循环周期非常接近。按照这一根据,由于下一峰值约在2030年,因此在近几年,我们会看到妇女获奖者人数的百分比会变得更小。
诺贝尔奖的未来
从前面的分析我们可以看到,虽然美国的占有率在2000年以前还是比较稳定的,但是每年的获奖人数已经开始下降。这将意味着诺贝尔奖的获得者的总人数也将下降。是否有理由认为诺贝尔奖励制度将会随时间的流逝而削弱或萎缩?
一些观察结果证明了这样一种推断。首先是每年的诺贝尔获奖人数正在增加。增添了一些新的获奖项目(如:经济学奖,和平奖),更多的人分享某项诺贝尔奖的越来越多。得奖者人数的增加率再不是一个常数了。这种膨胀式的做法将会导致贬值,由此而出现,每年的获奖人数增长率趋平并且开始下降,得奖的位置趋于饱和。
其次是诺贝尔奖获得者的平均年龄正在不断地增大。1940年以前,平均年龄为54.5岁,从1940年至今,平均年龄已经上升到57.7岁,如果我们只看最近十年,平均年龄已达到60岁。从自然规律来说这是一种退化,因为这里优秀和卓越是与年老和体弱相联系,而不是和朝气蓬勃的年青、强壮相关连。平均年龄增加的现象并不是唯一的。对美国来说,最辉煌的获奖顶峰时期是本世纪的30年代和50年代,这两个时期的平均年龄分别为51.1岁和49.1岁。
而且,图2所描述的竞争的动态过程与年龄的优势相吻合。1940年美国人赶上了英国人,前者的平均年龄为52.9岁而后者是54.8岁。同样,在最近的10年里其他“世界”的国家赶上了美国人,其平均年龄分别为57.3岁和69.3岁,此时,欧洲人的平均年龄继续上升,达到了62.4岁。
年轻,似乎比年老更具有优势,这样看来,授奖面随着年龄的增长而扩散,说明了这种奖励存在的必要性正在减弱。我们认为,这种现象的成因更多的是由于奖励常常迟滞于实际工作很长时间。这里使用了得奖时的获奖者年龄是因为这个年龄是现成的有效的,而且有时这个时间要比确定完成实际工作的日期更好更准确。然而,我们假设这种年龄的相对优势并没有什么影响,在三个地区国家组之间并不存在这种延迟的系统偏差。
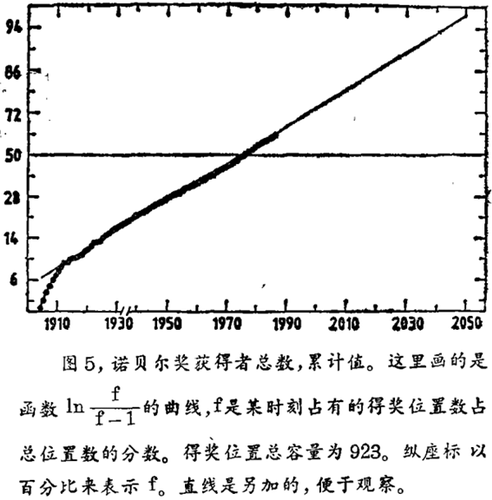
考虑了所有的问题之后,人们试图得知,获奖者的累积人数是否遵循逻辑增长的规律。就是说,这是不是一个趋向填满所有获奖位置的饱和过程。图5展示了变量ln[f/(1-f)],这里f是已经占据的获奖位置的分数。这一直线行为正是一个非常好的逻辑函数所描述的。确实,实际数据点的直线特性正好与此相吻合,在最底部的末端,有少许的偏离,这里f小于5%,在逻辑行为中是没有什么了不起的。
似乎诺贝尔奖的位置正好超过全世界所有时期的923个获奖者总数的一半。根据图5中给出的每年获奖者的比例,我们可以算出2050年将不到2。这个2050年的比例值还可以独立地从图1b和图2中获得、美国人一年的比例为0.2,是在同一年中占有全部比例的0.25的份额。这两个结果非常一致。从55年的周期性来看,可以这么说,诺贝尔奖励制度的生命周期为55年的3倍,即大约为165年。
或许,有另外一位诺贝尔先生,正在某地酝酿着一个新的奖励制度,这种奖励制度是建立在一种全新的优秀典型的基础上的,这种典型是与我们的认识大相径庭的。
[Technological Forecasting & Social Change,1988年9月]