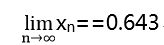（华东师大数学系）

当前计算机硬件不断翻新，个人电脑已进入寻常百姓家，比尔 • 盖茨的软件公司，拥有千亿美元的资产，已成为世界上最大的企业。数字化、网络化、智能化已成为一种全球性的发展趋势。克隆技术、基因工程、生物医学工程呈现令人鼓舞的前景。科学家们认为：21世纪将是信息科学和生物科学的世纪。在这样的时代，数字应该处于怎样的地位？新时代对数字有什么样的要求 ？

本文从本世纪80年代以来应用数学的发展来考察一下科技发展对数学发展的要求。

1.信息科技的发展需要数学建模

目前有一种流行语称为“电脑设计”，其实电脑是一种高速运算工具，所谓电脑设计全靠数学，例如利用空气动力学原理，工程师们可以在电脑上设计飞机；利用信号处理方法寻找有效的钻油井点；利用汽车的动力学模型，模拟汽车相撞以设计更合理的汽车结构；利用电脑和数学模型可以拍摄“铁达尼号”沉没，模拟核弹爆炸等。所有这些都离不开数学模型。

20世纪后期发展起来的虚拟现实（Virtual Reality）为人们提供了虚拟的环境。由它组成的飞机驾驶员训练器，可以使驾驶员坐在训练器中与坐在飞机上一样见到周围的蓝天白云，遭遇各种可能遇到的情况。用训练器训练驾驶员不仅成本低廉而且大大缩短了训练周期。人们戴上了与计算机相连的有显示器的头盔，可以在自己的住房内畅游故宫博物馆，其感觉如亲临其境。虚拟现实靠的是数学模型与快速算法，因为虚拟现实只有通过实时计算才能实现。香港在造新的候机大厅时利用虚拟现实来确定建筑方案。

2.信息科学的发展不仅为数学应用提供了广阔的舞台而且更需要数学创新

北大方正利用数学模型对于千变万化的汉字进行信息压缩，使排版印刷实现一体化，大大缩短了出版时间，对文章和图的修改、编辑提供了更大的方便，因此，方正印刷系统受到了大陆、港台、日本等使用方块字的出版机构的欢迎，不仅为我国创收外汇而且培养了一批具有创新精神的人才。

目下在计算机上输入语音信号获得初步成功。这就是说人们只要对着计算机讲话，计算机就能按人的要求运作。这样，作家只要讲出想写的文章内容，打印机马上就能打出文章来，然而要真正做到这一点，语音识别是一个重要的课题。如所周知，不同的声音是由不同频率的声波产生的，而语音信号不仅与频率有关而且与时间也有关。傅里叶变换只能提供信号的频率分析，不适用于语音信号的分析，于是小波分析走红了。

小波是一种只在有限区间上不等于零的波。利用小波分析不仅可以指出信号的频率，而且可以指出该信号发生在什么时刻。因此适用于语音信号的分析。

利用小波还可以进行图像的压缩与重构。这种技术使洛杉矶警局的指纹存储减少到原来存储量的二十分之一。小波具有局部性可用于信号的时频域分析和局部区域上函数的逼近。从傅里叶分析到小波分析是一种数学创新。这与傅里叶分析仍是一种有用的数学工具并不矛盾。

3.数学创新使数学进入了人工智能领域

我国著名数学家吴文俊首创的机械化证明和自动推理平台（软件系统），早期用于平面几何定理的证明，目前不仅能解微分方程、代数几何中的高深数学问题，而且能解决信息安全性等许多信息科学领域的问题。

90年代发展起来的KDD技术（数学库中的知识发现）早期称为数据挖掘（Data mining）。这种技术是在数据仓库、数理统计中的聚类分析、判别分析、最优化方法和机器学习等基础上发展起来的。KDD系统可以帮助人们，在大量的数据中找寻出原先未知的、蕴含着的知识、规律、规则和数学模型。因此受到了企事业单位的重视。

KDD技术中的篮子分析（Basket Analyeio）可以为超市提供最优的进货计划，预测市场的趋势；为银行提供有无坏账的信息；为生产质量控制提供最优工况应具备的条件等等，因此，近年来受到美国政府、欧共体的重视，被立为重点项目。

在这里可以看到，数学方法与计算机科学的结合是数学创新的重要途径。

4.混沌研究为我们提供了数学创新的新领域

混沌现象可以用非线性迭代方程（1）或非线性微分方程（2）来说明：

x_n+1=f（x_n），x₀=Z_0， n=0，1，2                      （1）

dx（t）/dt=f（x（6）），x（0）=Z₀                           （2）

其中f（•）为非线性函数。

举例来说，下列迭代方程

x_n+1==2.8x_n（1-x_n），x=0.1                           （3）

有一个渐近解，即

       如果把迭代方程（3）中的系数2.8改为3，那么x_n将不再有极限而趋向于两支（称为分支现象）。而该数大于或等于3.571448时x_n将杂乱无章地分布于第一象限两边与x轴y轴重合的边长为2的正方形之中，这便是混沌现象。混沌现象很难给出确切的定义，但其特点是明显的：

（i）混沌与分支产生于非线性系统；

（ⅱ）非线性系统的混沌与分支关于参数是灵敏的，稍微改变系数可使混沌现象消失。

某些心脏疾病会引起心肌乱颤，这可以看作一种混沌现象，如不及时医治会使心脏停止跳动。利用混沌现象关于系数灵敏的特点，只要在适当部位加以适当刺激注入某种药物可以使心脏恢复正常运行。

金融危机实际上是一种经济领域中的混沌，如果我们经常观察经济发展动态，及时进行小的调整，可以避免危机的产生。

根据最新研究，许多混沌现象是可以控制的。如何控制是一个值得研究的数学问题。

利用混沌与分支对参数的灵敏性可以使一个非线性系统在一种参数情形下派这种用场而在另一种参数情形下派另一种用场，从而组成多功能的器件或装置。人脑是一种多功能器官，毋庸置疑人脑具有某种产生混沌和分支的结构。1998年华东师范大学数学系承担的“同宿、异宿轨道的存在性、分支和混沌”课题研究取得重要进展，被列入上海科技进步报告。

5.生物科学不仅为数学创新提供了广阔的用武之地而且为数学创新注入了新的活力

生理解剖学早已发现了神经细胞及其功能，生物学家与数学家一起为神经元提出过各种数学模型。到80年代，由于BP网中反向传播算法和Hopfield网的发现，使人工神经网络的研究掀起了新的热潮，人们发现人工神经网络具有良好的“学习”功能，也是非线性函数的理想逼近，我国复旦大学陈天平教授关于人工神经网络逼近性能的研究及“Chen氏模型”，获得了IEEE Transaction on Neural Networks评奖委员颁发的1997年“杰出论文奖”和1998年上海市科技进步一等奖。

人工神经网络已经在非线性识别和非线性动态系统辨识中获得成功应用。

利用遗传基因的模式，数学家发明了解决非线性全局最优化的遗传算法。

此外，我国青年数学家、山东大学彭实戈教授的倒向随机微分方程理论为定价问题提供了有力的数学工具。

近来，国际天文联合会（简称IAU）宣告：2028年10月将有一颗小行星掠过地球，与地球相距只有3万英里。然而根据Yoemans和Chodas的计算表明，2028年10月掠过地球的小行星离地球60万英里。两种结果相差20倍。那么这个小行星掠过地球时究竟离地球多远，值得人们关注。

综上所述，21世纪已在眼前，信息、生物、工业、农业都提出了大量的数学问题，而问题的解决往往需要数学创新。

虽然信息科学与生物科学是21世纪科技舞台上的主角，然而数学绝不是无足轻重的配角。数学对于21世纪这个科技“舞台剧”来说，它是京剧里的“程式”，话剧中的“台词”，是这个“舞台剧”中不可缺少的元素。

21世纪是一个科技迅猛发展的时代，科技发展需要更多的数学创新，现在许多高科技问题得不到解是由于其数学模型尚不清楚或还没有相应的数学方法。数学创新是时代的要求。