在这个二十世纪最伟大的物理学家的百年诞辰纪念会上讲话,我感到十分荣幸。
我讲演的题目是几何和物理学。几何是一门起源于对形状和大小作定量研究的科学。几乎在所有的文化中,人类都迷恋于几何学。这或许是人们认为几何结构在艺术中起着重要作用的一个基本理由,我们已从Shapiro教授昨天的有趣的讲话中知道了这一点。几何结构也在物理学定律中起着重要的作用,这是一个众所周知的事实,虽然关于这件事的准确理由并没有被真正理解。今天下午,我想向大家描绘一下几何学在当代物理学中所起的错综复杂的作用。
爱因斯坦在他1946年的《自述》中曾说:
“在我的学生时代,最使我着迷的课题是麦克斯韦的理论。这理论从以超距作用力过渡到以场作为基本变量,从而使它成为革命性的理论。”
用今天的符号来写,麦克斯韦方程是:
这些定律的经验基础是物理学家从十八世纪后半叶开始的几乎一个世纪内所作有关电和磁的基本实验推导出来的。由于熟悉这些定律,法拉第(1791 ~ 1867)得以创造出力线的几何概念和场的概念。法拉第是一位具有深刻的直觉能力的实验物理学家,但他不太精通数学,并没有用数学语言写出他关于电磁的概念。关于他,海姆霍兹曾经写道:
“这么大量的普遍定理,它们的有条理的推导需要最高度的数学分析能力,可是他却凭一种直观,凭直觉的可靠性,而不用一个简单的数学公式竟然发现出来,这是十分令人惊讶的。”
虽然法拉第发明了场概念,但是发明“场论”这个术语的荣誉,却属于麦克斯韦(1831 ~ 79)。在181865年,麦克斯韦发表了一篇论文,它理应被认为是上个世纪物理学中最伟大的一篇论文。论文的题目是:《电磁场的动力学理论》。其中的两段如下:
“因此我提出的理论可以称为电磁场理论,因为它必须处理电体和磁体的邻近空间,它也可以称为动力学理论,因为它假定在那种空间中有物质在运动,通过这种运动引起了观测到的电磁现象。”“电磁场是包含并围绕那些处于电性和磁性条件的物体的那部分空间。”
从论文的明确的陈述看来,麦克斯韦的计划就是要以数学的公式写出法拉第已经作为物理观念而想到的东西。在他写作论文的过程中,一旦他把经验定律具体化为方程的形式,他发现有一些前后矛盾的地方,这些只能通过加入“位移电流”才能够消除掉。这一发展具有巨大的重要性,并且说明了直觉常常是多么的不够。精确细致的数学公式是有决定性作用的,因为有了它,人们就能够运用充分发展的数学形式工具来处理问题。
在他加进了位移电流之后,麦克斯韦进一步证明他的方程允许波动解。他推算出波的速度并把它与观测到的光速相比较,得到了十分惊人的结论:光传播就是电磁传播。
当时他所表露的激情可以从他在1861年写给凯尔文勋爵的信中的一段话感觉出来:“在我对磁效应传播速度和光速的数值相近有任何猜测之前,我就在乡下发现了这些方程,所以我认为我有理由相信磁介质和光介质是同一个东西。……”
麦克斯韦曾经告诉法拉第(他比麦克斯韦大40岁),他自己致力于用数学形式来表达法拉第的物理观念。法拉第赞慕年轻的麦克斯韦的努力,但并不十分愉快;正如一个真正的实验物理学家所应该是的那样,他有一点儿害怕太多的数学形式。他害怕太多的数学形式会损害他的物理观念。他的态度生动地表露在他1857年写给麦克斯韦的一封信中:“我亲爱的先生,我接到你的论文,为此深为感谢。我并不是说我要感谢你是因为你谈论了‘力线’,因为我知道你已经在哲学真理的意义上处理了它;但是你必然以为这项工作使我感到愉快,并给予我很大的鼓励去进一步思考。当我看到构造这样一种数学的力来针对这样的主题,起初我几乎是吓坏了,然后我才惊讶地看到这个主题居然处理得如此之好!”
许多实验物理学家今天同样对接受在理论物理学家的语言中愈来愈流行的很深奥的数学感到犹豫不安。
麦克斯韦谈到了光介质即以太。他这样做是十分自然的,因为在麦克斯韦的时代人们所考虑的主要是力学模型,而力学模型当然必须构造在一种介质之中。
“在我看来,对‘我们是否理解物理学中的某一个特定的论点’的检验是‘我们能否作出它的一个力学模型!’”
麦克斯韦遵循时代的信仰,设想了很复杂的力学模型来解释他所得到的方程。他对这些模型的态度是很矛盾的。在有些地方,他明确地说这些模型是不必要的和仅仅是教学用的,而在另一些地方他明确地说介质一定是有的。
爱因斯坦在他的《自述》中涉及到这些材料,并且问他自己:为什么物理学家们是如此难以摆脱注定的以太观念?他的结论是,在十九世纪,传播必须有一种介质来支持,而“真空”被认为正是“介质”的一种特殊情况。
麦克斯韦方程被许多物理学家所研究。他们之中有赫兹(1857 ~ 1894)、洛伦兹(1853-1928)和彭加勒(1854 ~ 1912)。一个特别重要的发展是洛伦兹变换(保留麦克斯韦方程不变的数学替换)的发现。但它需要爱因斯坦的天才来告诉物理学家这种变换的精确意义。
智慧如彭加勒,博学如洛伦兹,都不敢迈出决定性的革命性的一步来重新审查我们的同时性概念,这种概念也许不只是从我们的父母那里学来的,而是在我们的基因中通过百万年的进化而遗传下来的。
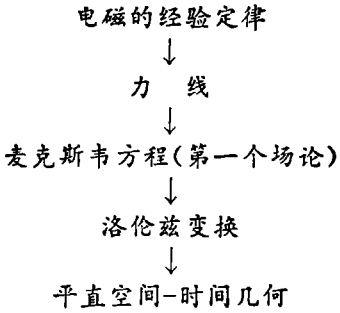
总结起来,我们可以把上述历史进展图示如下:
人们从电磁的经验定律开始,导致法拉第的力线概念,它一旦纳入数学形式,就得出麦克斯韦方程。而后者又促成了场论的诞生,它至今还是今天的物理学中的中心议题。麦克斯韦方程导致洛伦兹变换的概念,通过爱因斯坦的工作,揭示了平直的空间 - 时间几何。
由此作出一个特别重要的结论(它是由爱因斯坦果断地作出的)是,对称性起着一种特别重要的作用。在1905年以前,方程是从经验推导出来的,而对称性又是从方程推导出来的。然后,——爱因斯坦说——闵可夫斯基作出了重要的贡献使事情倒转过来。首先你宣告对称性,然后你寻求与它相符合的那些方程。
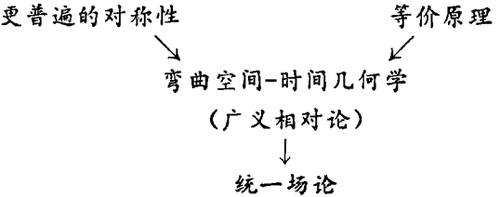
这一观念在爱因斯坦的心目中深深地扎了根,并且从1908年以来,他就要推广它,把对称性本身扩大为更大的一种对称性。他要求普遍的坐标对称性,而这就是导致广义相对论的动力之一。另一个动力就是等价原理的物理观念。把这两者结合在一起,并就此奋斗了七年多,他终于在1915年给予世界一个弯曲空间 - 时间几何学和广义相对论。
广义相对论是一种场论。爱因斯坦深'深地为他的这个独特创造所感动,并强调应当在这个基础上建立一个能包括物理世界更多东西的理论。在当时,在引力作用之外,只有另一种众所周知的相互作用,这就是电磁相互作用,因此他要建立一个关于这两种作用的统一场论。
在这个研究题目上,他耗费了他绝大部分的余生。在《相对论的意义》的最后一版中,他增加了一个附录,其中他提出一个具有非对称张量gμυ的统一场论。张量的反对称部分要等同于电磁场张量Fμυ。这种努力不是特别成功的,因而有一个时期在某些人中就有这样的印象,似乎统一的观念是爱因斯坦老年时期影响他的某种固执的观念。诚然,这是一种固执的观念,但是这种固执观念是与对理论物理的基本结构应当是什么的深刻理解相联系的。而我还要补充一点,这种深刻理解更是今天物理学研究的课题。
不管怎样,这种对统一的强调,立即产生了某些结果。它引导许多杰出的数学家[包括勒维 - 契维塔、卡旦(Cartan)和魏耳] 更深入地寻求对空间 - 时间的数学结构的可能补充。
魏耳曾经努力尝试把电磁和引力结合在一起。他的观念导致所谓的“规范理论”。这一发展的时期要回溯到1918至1919年。魏耳设想,既然坐标不变性的适当处理产生了引力理论,一种新的几何不变性也可能与电磁相联结。他的创议是标度不变性:如果xμ和xμ+dxμ是两个彼此邻近的空间 - 时间点,又如果f是某种物理量,它在xμ是f,在xμ+dxμ是
现在魏耳观察到两点。第一,Sμ和电磁势Aμ有同样数目的组元。第二,通过进一步的发展,他证明:要求理论在标度变换时不变,只能有Sμ的旋度出现,而不是Sμ本身出现。这也是Aμ的特征。所以他把Sμ等同于Aμ。
可是这一观念并不成立。有几个人(包括爱因斯坦)讨论了这个问题,爱因斯坦证明魏耳的理论不能描述电磁,魏耳就放弃了这个理论。
后来到了1925年,完全与这方面的进展无关的量子力学被发明了。
我们大家都知道,在有电磁的情况下,在古典力学中出现的不是粒子的动量p,而总是组合
这是一种相位变化,而不是一种标度变化。因此,局部相位不变性是电磁的正确量子力学特性。
魏耳自己最初叫他的观念为“量杆不变性”(Massstab Invarianz),但是后来改为“度规不变性”(Eich-Invarianz)。在二十年代初,它被译成英文,叫做规范不变性(gauge-invariance)。
如果我们今天要重新命名它,显然我们应该叫它相位不变性,而规范场应当叫做相位场。
一旦人们理解了规范不变性是相位不变性,人们就发现关键的观念是不能积分的相位因子。用更复杂的相位,即一个李群的一元,来取代简单的复数相位,引导人们走向非阿贝耳规范理论。
可是在历史上,非阿贝耳规范场概念并不是这样起源的。而是起源于下列两个来源。
其中之一是局部对称性概念,它是很简单地走上这条道路的。我们知道质子和中子是很相似的,它是构成一个同位旋双重线。它们并非完全一样,因为一个是带电的,而另一个不带电,又因为它们有微小的质量差。然而每个人都相信,如果人们能够去掉电磁相互作用,它们就会变得真正等同。现在让我们进入这样一个世界。我们可以叫一个核子为质子,叫另一个为中子,但叫哪一个是中子、哪一个是质子是一个约定的问题。事实上,我们可以取两种状态的任何线性组合,并采取一种约定叫它为质子,并称正交于它的状态为中子。于是产生了这样的问题,是否在这个房间中这种约定的选择是同在另一个房间做实验的人相关联,也就是说,是否在不同的空间 - 时间点的每一个观测者都可以独立地选择约定。
如果你相信约定应该互不相关地被选择,你就不得不构造一个理论,它允许点到点的约定自由。那么你自然而然地得到了一个SU2非阿贝耳规范理论。
第二种导致非阿贝耳规范理论的动机如下。在五十年代,我们大家都知道人们已经正在发_现各种类型的介子,它们具有不同的质量、自旋、宇称和同位旋。所以人们忙于试图写下有关它们的相互作用。只要求与洛伦兹不变性和球内部不变性(同位旋)相符合,就有大量被允许的相互作用,因而也没有普遍原理可据以在它们之中作选择。另一方面,任何新粒子的电磁相互作用总是以唯一的方式通过p-(e/c)A的处方被规定下来。这就是说,人们认识到,一旦你有一个守恒量(在电磁的场合是电荷)规范原理允许你以唯一的方式写下相互作用。因为除了电荷还有其他的守恒量,例如同位旋,所以问题就是:“我们能够以完全相同的方法把同位旋双重化吗?”在尝试这样做时,人们得到了普遍非阿贝耳场。
立刻可以看出,非阿贝耳规范场与麦克斯韦场相反,有一种值得向往的性质,即是非线性的。因此它可以在没有外部源泉的情况下产生它自己。爱因斯坦曾经反复强调我们需要非线性的场论。
非阿贝耳规范场论的另一个吸引人的特征是直接与上述第二个动机相关联的。它允许人们用一个耦合常数写出各种相互作用,这是今天试图把一切强、电磁、弱作用统一起来的中心课题。
我们今天离那种统一还十分遥远,但是近六年的实验已经显示它们与弱作用和电磁相互作用统一的特殊模型惊人地吻合:这就是温伯格 - 萨拉姆模型。这个模型有两个概念上的要素,一个是非阿贝耳规范理论,另一个是破缺对称。
破缺对称的概念是很得心应手的。人们必须适应自然界是不完全对称的事实:质量和耦合常数并非全是一样的。破缺对称机制允许人们有这样的理论,其中相互作用的拉氏函数具有完全的对称性,而它允许不完全对称的实验表示。人们在晶体中找到一个破缺对称的例子。晶体的哈密顿函数有完全的转动对称性。这种对称性在液相中是显然的。但是在低温时,系统变成为固体,它在物理上不再是转动对称系统。换句话说,方程的对称系统,通过对称破缺机制,产生不对称的实验表示。
温伯格和萨拉姆在1967 ~ 1968年把规范场观念和对称破缺观念结合起来,构造了一个统一弱作用和电磁相互作用的模型。令人注意的是它的结果与实验符合得很好/虽然从理论观点看来,它只是许多可能的模型中的一个。
我要强调指出,正如在统计力学中一样,在一个破缺对称模型中缺少完全的对称性是一种低温效应。用这种观点看来,在做通常的高能实验时,我们总是探查零度温度的破缺对称规范理论。不管能量多么高,初态总是在零度温度准备的。因此,完全的对称性从来没有在任何能量时实现。可是,假如我们能够到达一个足够高温的体系,我们就会看到恢复完全的对称性。这是令人满意的,因为这意味着,完全的对称性在原则上可以直接用实验来检验。
也已经有人尝试建立强作用的规范理论,在这方面,以后我们将在这次讨论会中听到许多讨论。
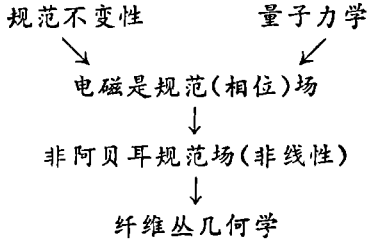
回顾前面关于规范场的历史渊源的画面,我已经在其中列举了物理学家认为在描述实验定律时是必要的那些概念的发展。寻求这些概念的动机渊源于物理现象。因此十分令人惊讶的是人们发现规范场概念等同于叫做纤维丛的几何概念,它是由数学家完全独立地发展起来的,与物理实在没有任何关系。
规范场是一个几何概念,这不仅是正确的,而且其结果是拓扑复杂性对于规范场也是重要的。对这一点的重视是来自狄拉克的磁单极,特 · 霍夫特(′t Hooft)的单极子和贝拉维安(Belavian)的膺粒子解。事实上,正是通过例如由狄拉克的磁单极所必需的拓扑复杂性,才使我变得绝对相信:像麦克斯韦场那样的规范场,不仅可以用纤维丛的几何语言来表示,而且必须这样来表示,才能表达它们的全部意义。
本世纪物理学中基本概念的发展已经纳入了深刻的数学概念的框架。
在这个表中,我们没有列入以数学作工具解决物理学中数学问题的那些应用。
可是,如果认为数学和物理这两个学科重叠得如此之多,那是不对的。它们有明显不同的价值判断,它们有不同的传统。在基本的概念层次上,它们令人惊异地共享某些概念,但即使在这里,每个学科的生命之力仍然在它们各自的血管中奔流。
————————
* 这是杨振宁教授于1979年3月20日在耶路撒冷爱因斯坦诞辰一百周年纪念会上的讲话——译者