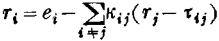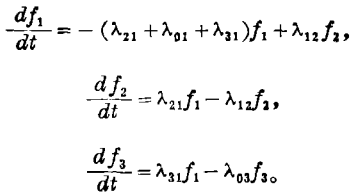[提要]本文概述了现代数学,特别是微分方程和生物医学之间的联系,生物医学的发展愈来愈需要现代数学,同时它又给现代数学的发展以新的推动。最后还提出了达到两者结合的三种途径。
几年前,Eugene Wigner就讨论了“数学在自然科学中的不合情理的作用”。确实,数学在物理科学中取得的成功使得可以声称它为女皇或女仆。如人们所知,生物科学的情况还未发展到如此程度,然而也已涉及数学的不合情理的作用。Wigner已经观察到“能够预知其功能的机械造就了物理学家的最卓越成就”。生物学家还尚未探求这种创造,给了他机器,他必定会去分析机器的,他也喜欢预知机器的未来功能,但是他被系统化现有的知识的任务紧紧地困住了。也许这就是以数学的方式来了解生物现象发展迟缓的原因。
当然这并不意味着数学全然没有进入生物学和医学。事实上,在各个领域人们都能发现借助于各种不同的数学技术不同程度地以公式来定量表示,这不是最近出现的。Euler曾论述过血液流动和死亡问题。其它重要的数学家——Descartes,Helmholtz,Volterra,Von Neumann——处理过生理学、生态学和生物学其它分枝中各种各样的问题。但是翻阅一下揭示药物学中的药品吸收方式、形态学和胚胎学中的生长率研究的医学手册,它们几乎未能涉及到最近一个世纪以来的数学流传下来的成就。多年来,在数学生物物理学的特殊课题中已经进行了些工作。当然,事实是数学已在物理学中起到了核心作用,相反,它还没在生物学中起到中心作用,生物学也没起到促进更多更新的数学思想的作用。
随着定量测量技术和实验控制的大量增加,情况将会很快改观,在许多生物学研究领域中现在可以用变形法高速度地获得数据。例如,在洛克菲勒大学H. K. Hartline实验室里一架小型高效的实时数据处理系统,不仅能使呈现在鲎眼睛里的运动的光图像,用测量神经冲动的发放来解释,而且能快速地分析反应的频谱和噪声特性,借助这种功能已获得了大量的数据分析和数学模型。这样,反过来又产生了许多数学理论,并肯定能促进更多更好的数学理论的产生。计算机的应用显然起着巨大的作用。能有更多的数学家从事生物学和医学研究和更多的生物学家都来了解数学的公式和数学技术,这显然也是很需要的。
下面简要讨论几个例子,企图表明像数学在物理学中的应用一样,把生物学和医学作为数学应用的新领域来描述(不是讨论),而不是作为统计技术或数据处理的应用。
我们将数学研究分为三方面。首先,我们讨论某些经过严慎验证的数学公式作为重要的生物学理论的条件。在这些公式中,数学家的工作是进一步利用和发展这些公式。后面要稍加描述的具有非线性扩散方程的神经冲动传导理论就处在这一阶段。其次,数学家的工作是协助构造数学公式,他根据已具备的资料、生物学的理论以及公式化的方法来进行工作,并从事于建立模型。狗身上做的碘代谢模型就是作为这一类型的例子来讨论的,称之为间隔分析。我们讨论的问题还未达到这一阶段。最后是各种数据分析和数据处理的数学工作,不在这里讨论。正如人们可以预料的,统计学、时间序列及其它图形分析等都是属于这方面的数学方法。
—个有趣的观察是数学处理最先进的那些领域,如神经传导问题或动脉血流问题,和生物力学联系最为紧密,而和临床医学所用的应用生物学相距甚远。真如我们通过数学公式将数学技术应用于统计学和资料分析一样,我们也可以这样把纯生物学推向医学。
这些数学对生物学的渗透会不会产生新的数学?仍待阐明,至今,虽然存在新的特殊问题还没有新的数学科学手段,但是有些新的科学手段目前似乎还不需要它们。人们可以想象现在已有了一个庞大的备用的数学工具仓库和大量极端复杂的生物学中待研究的问题,所需要的是如何把这些问题用数学语言来描述,这本身是一个艰巨的任务,如果这样做了就有可能出现新的数学。
概 述
在我们较为详细地讨论例子前,简要地列举数学在生物学和医学中的几点应用,后面不再讨论:
1. 在研究如同脑这样大量的神经细胞中,“神经网络”的数学描述已经有了设想,所用的数学工具包括有逻辑方法和布尔代数的方法。
2. 多年来,在弹性管中的粘液流动已经作为血流的模型,采用数学的方法来加以研究。现在,对于考虑动脉和静脉分枝处阻抗匹配的模型也正在改进。同时,刚能通过毛细血管的细胞的流动正得到更正确的处理。
3. 把心脏表面的电势和心电图上电压记载联系起来的势论的应用,现在正有助于搞清心脏运动和胸壁厚度在这些记录方法上的作用。
4. 超速离心机的定量使用,要求应用非标准簇的非线性扩散方程。
5. 比以往任何时候都进行得快得多的复杂的富里哀高速分析,对X射线结晶学来说仍然重要的,这种X射线结晶学能帮助阐明如血红蛋白,肌红蛋白,溶菌酶,糜蛋白酶的大分子结构。
6. 非常有用的计算机现在能够计算通过病人身体的射线的分布,此病人或接受几种射线照射或被植入放射源,通过计算允许我们修改放射治疗使之更符合医学上的需要。
7. 了解正常和功能不全的二种血液系统中白细胞的生长周期,对白血病有着重大关系。现在,各种模型均在使用中,可以预料同步细胞的生长问题可以突破。
8. 单细胞的力学推动模型——纤毛,鞭毛,或伪足——已经合理而成功地得到发展。
9. 为了把物理结构和可观察到的脑功能联系起来,应用代数拓扑学的方法(特别是容许空间理论)已经提出了一个有趣的模型。这是一个定量的理论,是现代几何学以它的拓扑学形式在生物医学中的一种应用。
生物学理论和神经生理学的数学处理
有极少几个生物学问题已经获得足够满意的数学描述,致使数学处理成了有趣的和有价值的研究。为了展示已经提出的几种问题,首先让我们考察一下来自神经生理学这一特殊领域中的几个问题。
神经冲动传导 在神经系统中信息是以电脉冲的形式沿着单神经纤维传导的,描述脉冲传导的一整套方程式是由Hodgkin和Huxley研究的,并赢得了诺贝尔奖。
简要地说,沿着单神经纤维膜传导的电位符合一非线性偏微分方程(见表1)。除了问题的多种解答需要讨论以外,这方程式在描述神经纤维行为的许多方面都是非常成功的。为了扩充和推广这种模型已经做了许多工作。
乌贼的某些神经纤维大得能非常正确而精细的测量和重复测量,对于这一模型提供了第一手的资料。表1的方程(2)对乌贼的所有纤维长度都适用。脊椎动物的神经纤维绝大部分覆盖着称为髄质的一层组织。方程(2)到(5)描述的离子交换,仅适用于神经节(例如,蛙的某些神经纤维,神经节之间的距离仅为2毫米,传导的脉冲波长可跨越20个神经节)。在这一例子中髓鞘部分Ii与v(x,t)有线性关系,方程又适用于神经节。修改后的Hodgkin-Huxley方程在蛙的髓鞘纤维得到验证,再次发现是非常满意的。
更详细的数字检查这个模型证明非常成功。
1. 若给一个阶梯电流刺激且保持恒定,阶梯电流的大小将决定脉冲的重复速率,事实上这就是振幅对频率的转换关系。神经细胞以这种关系传递强度信息。
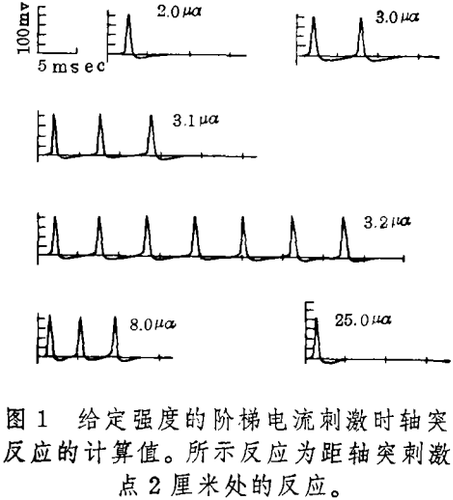
2. Hodgkin-Huxley系统的特点是:对仅仅阈上的电流刺激强度而言,就出现一串有限的脉冲,当刺激强度增加时,脉冲数目随之增加到极大,随后刺激强度进一步增大时脉冲数目便降低,如图1所示。这基本上是和实验结果相符的,仅有几点重要细节不同:
a. 脉冲数目到达极限的刺激强度范围是非常小的,它小于人们所预期获得的实验所得的范围。
b. 虽然实验显示出脉冲间隔是随刺激强度的增加而缩小,而计算结果却没能以任何方式显示出来。
最近,试图了解一下当分枝到肌肉末端的神经纤维时,模型能否给出神经冲动的正确行为。冲动传导是否延续到较小的纤维末端,现仍在实验中,近似的计算也将完成。
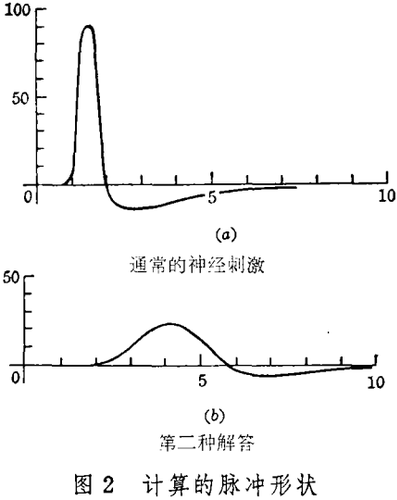
多种解答 数学家和生理学家都感兴趣的是能够得到几个解和有几个解能满足表1的方程。因为良好的初始神经冲动具有固定的波形,并沿神经膜恒速传布。偏微分方程的近似解必定接近于维持传导波形式v(x,t)=v(x,θt)。这样,偏微分方程就转换成了常微分方程。(这样处理和先前描述的脉冲形式相差较远),常微分方程的初始解由θ值的选择而定,从神经的远端开始积分到另一端,不同连续行波导至一个非常满意的神经脉冲,脉冲的波形、大小、速度均可与实验结果相比。且未被实验观察到的另一结果也发现了。(见图2,曲线a的上一行是通常的神经脉冲。)
若一恒定的行波假设还未做出,对偏微分方程的初始值可由微分方程的近似解得出,并就以这样形式得到解决。以这种方法可观察到脉冲的产生以及脉冲以恒态传布的方式被研究。非常满意的看到,这些分析给出了一个实验(提供适宜的阈上电刺激)所发现的稳定状态,且如第一种分析所预示的那样。
然而,当刺激强度略低于阈值(化学条件正常)时,计算得出像图2曲线b的脉冲。在这种模型中,脉冲不能延续得非常远(取而代之)很快就衰减了。这样,我们必然会问:a和b是稳态传佈解还是不稳态传佈解?在一根神经上我们能观察到不稳态的传佈吗?我们还不知道第二个问题的答案,虽然用普鲁卡因药物和适当的刺激相结合能减弱它的衰减直到实际上观察到不稳态的脉冲为止。
方程式的另一用处是能计算出加在有髓鞘纤维上的药物和毒药剂量,这一想法是利用模型的实验、化学、电资料来计算在传导速度和其它特性上药物的作用。在这一问题和其它几个生物学问题上所显示的数学和生物学的相互作用已足以使我们去设想如何研究新的生物学现象。
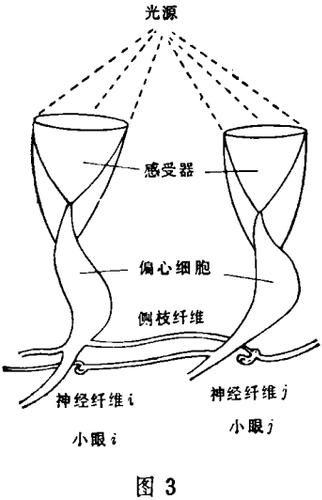
感觉接受 我们已经讨论了信息如何沿着神经纤维传导的问题,但我们还未讲到它们是怎样产生的。Hodgkin-Huxley模型没有涉及到这类问题。让我们回到一系列有名的取自于鲎眼的实验,这是洛克菲勒大学H. K. Hartline实验室所发展的理论。Floyd Ratliff新近的一本书中给出了一个非常有用的观点,鲎的眼睛为复眼,含有上千只固定的感受器小眼(图3)。每一小眼和一单神经纤维相连,每一感受器——纤维对提供光感受和产生神经脉冲的一个简单通道。人们可以设想,一束小眼和其它直接观察到的神经纤维连结在一起代表一个非常原始的视网膜。
当一束光照射在小眼的晶状体时,在它的神经纤维上就产生一排电脉冲,这时刺激小眼周围产生的脉冲速率就有很大差别,这种相互依赖关系,称为旁侧抑制,在各类感觉系统都能发现。
在鲎,刺激旁的感受器总会减弱给定感受器的信号。当光图形保持恒定时,这种减少可用Hartline-Ratliff方程表示:
式中(rj-τij)必须大于零。τij为第i小眼刚刚对第i小眼有作用时的阈值,周围神经纤维的实际速率必须超过此阈值才有效应。κij为感应系数,它测量作用的强弱。式中ri是观察到的神经纤维i上的脉冲速率,而ei是仅仅光照感受器i所观察到的速率。
在实验中,需测量的量是ri和ei。假如我们掩蔽所有周围的小眼,光线仅照射单一的小眼,ei即可测得。移去掩蔽物,ri就可测得。实验能发现一对小眼之间的相互作用,且能十分可靠地确定小眼之间相互抑制的阈值。
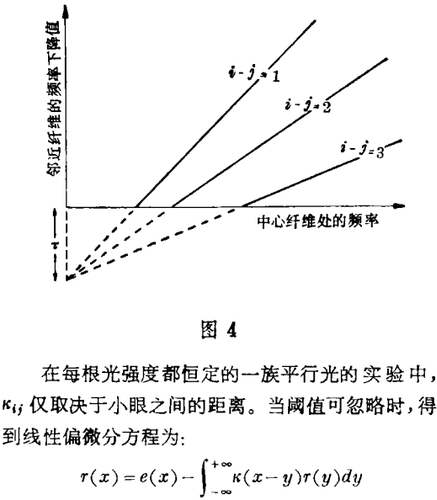
当仅一根旁的小眼不掩蔽时,旁侧抑制问题就可被研究,当二根小眼之间的距离i-j增加时,相互作用κij的强度就降低,阈值τij增加(图4)。这仍然是一种推测。事实上,阈值仅简单地与κij有关:τij=τ/κij,这里τ如图4一样定义。
对于核,κ(x-y)由于κij取决于距离而可相当简单地测定。当r(x)和e(x)的值被取代掉,κ(x-y)的确定仅和二个小眼实验所确定的值有关。(试图处理与阈值有关的在τij=τ/κij假定下的适当数量的小眼,例子导致了一个非凸二次程序问题,问题尚未得到解答。)
问题的陈述:功能的间接测量
现在我们来考虑生物研究的某些例子,在这些研究中,数学的陈述使数学工作者为难。这里,数学家发现他们自己的工作是和生物学家获得的资料紧密相关的,用物理、化学的原理及生物学的经验表示出试验关系,用分析和计算来检验它们,于是再返回来提炼。一般地说,数学技术上的困难相对于数学陈述上的困难是次要的。
严格的定量的生理学深深地产生在机体组织内,直接的测量常常是困难的和不可能的。所以,若人体的测量在诊断上是特别有用的话,常常必须去解决直接的测量,这种测量几乎必然要立足于数学模型。目前,提供给生理学直接的方法是很重要的,这通常是它对重要的量和过程的唯一测量工具。
间隔分析 这些问题大部分是取自放射示踪实验的数据分析。称为间隔分析或合并理论的这些问题是电路综合中的黑箱方法,或者是经济学中的输入输出分析的相似物,它们已用公式表达出,并已研究了多年。
在各种情况下,一般讲方法是相同的,把物体可分为“间隔”(这些间隔相互之间可以或不可以物理地分隔),对物体内的某些物质进行分析(一种元素、一种离子或一种化合物)。二个简化的假定如下:(a)每一个间隔不断保持混合,以使每部分的物质的浓度是一样的。(b)认为间隔对物质能够以比例于它的第一段间隔的浓度的速率从一间隔流到另一间隔的方式彼此连通。(这种流动通常可以是但不必须是以不同速率的二种流动方法。)当每一段间隔中物质浓度的变化速率等于进出总量之差时,这模型就成为一(线性)普通偏微分方程系统。间隔足够多时,模型就能够十分接近真实情况。
假使模型已建立,并成功地符合于资料。那么需要间接测量的是什么呢?在总血流量的情况下通常主要关心的是从一间隔转换到另一间隔的速率和间隔的“尺寸”,对直接测量可以不受影响。
一旦模型被建立,并且在受影响的那些段间隔中的浓度有足够的历史数据被收集到手的话,有用的计算程序即能被用来算出符合模型的参数,通过计算再计算,直到掌握的近似最佳值。当这些参数以最简方式,即线性方式进入偏微分方程模型时,它们以非线性方式进入历时,因此,由于生物的自然差异的影响及不可避免地测量误差的影响使得涉及到更多的困难。结果使得没受过数学训练的生物学实验者不能单独地、完全自动地使用计算程序。关于合适类型和适当的数据的问题要求在曲线拟合过程开始前就需确定待解的未知数。另一方面,有关可能的重要交换通路的问题,需要生理学家的看法。
在许多放射示踪的生理实验中采用线性模型,因为有关更复杂模型的机理了解得还太少。即使在膜转换的研究中,线性间隔模型仍是十分有用的。然而有大量的化学运动问题本质上是非线性的。酶动力学方面已经做了许多工作,新近有许多这方面的工作得到计算,包括红血球和其它身体组织之间的铁转换问题,要求非线性的偏微分方程模型。
一则实例 在研究碘(实质上是碘离子)如何在狗身体内运动时,重要的问题是考虑包含主要产生甲状腺的甲状腺素那部分系统,在其中碘与蛋白结合着。一个典型的实验着手于给狗以足够大剂量的碘化钝,使甲状腺及身体其它组织都被非结合碘所饱和,事实上,这使甲状腺不活动,于是被作了标记的甲状腺素就引进到血液中,一部分甲状腺素在体内循环并扩散到身体细胞内,在细胞内即发生新陈代谢过程,然后作为甲状腺素再回到血液内。另一部分甲状腺素在血液内成为非结合碘,而一部分甲状腺素以结合的形式从肠和内脏排泄掉,游离的碘化物经过肾从尿排泄掉。
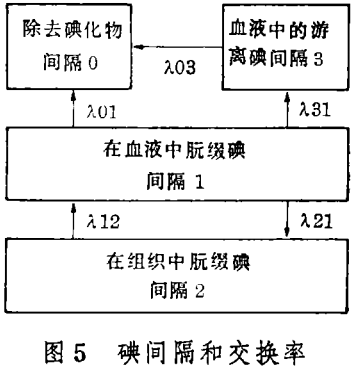
在一典型的首次试验模型中,血液循环和扩散过程(通过血液及穿过细胞膜)发生得非常快以致几乎完全扰乱了。假如我们仅需要把狗分为“血液”和“组织”,假如我们能忽略组织中游离碘的存在,因为无碘化物是从非朊缀状态转换而来的,那么一般的图解如图5所示。
在一个仅仅做血液测量的实验中,数据可以从血液样品中每单位体积内总的放射数获得,并且同样的测量也可取自于样品中沉淀的甲状腺素,这些可以转变成注入放射量的片断,使得能测量(标记,碘)在已知的时间间隔内的百分浓度。因为标记碘在狗身上可以像无标记碘一样以同样精确的方法来处理。图5所示比率常数像应用在总碘化物一样很好地应用于标记碘化物。
若fi为间隔i中标记碘化物的数量,ki为间隔的(有效)尺寸,qi为每单位体积的标记碘化物浓度,于是
fi=kiqi
而相应于图5的微分方程为
当初始条件(在时间t=0时)为f1=1,f2=0,f3=0时,这些方程式可以很方便的以fi的形式写出。
因为只有q1和q3可测,k2和q2无需分离地考察,而仅需估计。(k1和k3需是不同的量,虽然二者都涉及到一个“血液”间隔,因为游离碘比朊缀碘能更快更广地在体内扰乱,)当这些系数估计出后,通过使用初始条件和测量数据,它们将能提供转换速度和间隔体积的测量值。为了扩展它使其适合观察浓度是可以的,它将进一步提供这种简单模型的合理性的依据。
当用David Becker博士和在Cornell医学院的同事所获得的资料时,所讨论的这种模型事实上是很成功的。在一系列狗身上获得了转换速度,且关系完全一致。
呼吸 对呼吸系统化学元素的行踪已给出了一个相当广的数学公式。这模型再次使用了常微分方程,它忽略明确的空间依赖关系,只引入时间延迟和说明转换或对流与扩散时间的微分方程,对一心肺行为的模型,气体压力可以在血液和肺内,作为模型的输入输出数据而测得。在此工作中引入了控制论概念。
某些这类系统容纳了全部血流区域——心,肺,脑和身体其它部位,而另外一些却集中在特殊的交换区域。例如,在肺泡里气体交换和血液对流之间的关系已经被考虑,列出了方程式,并找到了计算方法。在这种情况下,因为气体容量和压力很容易从病人身上测得,有理由相信:对模型的高速度计算,甚至线性的计算最终可以产生一种临床诊断呼吸功能不全的有用工具。
教学和合作
虽然各生物学和医学领域已经涉及到这些主要的样本,并且相当水平的数学已力图在某些方法上显示出来,但很清楚,还有许多事情要做。数学家现在从事生物学问题研究的理由是明白的。数学家能够如此做的,然而不是简单地能达到的。似乎有三个主要方面可供选择:
1. 数学家可以进到实验室、医院和医学院,使他能获得实验和数据的直接概念,并且在局部领域也能成为一个行家。
2. 一个生物学家可以进入数学系,在那里他可以学会公式表达和运算的技术,并贡献他的知识,迫使数学家去研究那些不可测量或其它笨重的工作。
3. 数学家可以不进入这些联合安排,但他可以利用这些领域的丰富文献而以较为独立的方式使数学家进入生物学。
在所有这些方法中,重要的问题是数学家尝试去创造某种道理和判断,使他在许多他陈述过的问题中选择他继续工作的方面。在已经确立的数学应用领域——流体力学和固体力学,电磁理论等等——这种判断已由多年的相互联系和贡献而抚育着。在生物学方面,现在最好是诱使在特殊的生物学领域中的专家,他已经能使用某些数学方法,暂时成为数学家集团的一个成员,并集中他的注意力在数学公式化上,并解决在他的领域里所提出的数学问题,困难是要保持生物学家的“韧性”,保持他在他的领域中的活动性,在某些情况下这种尝试是成功的。这部分取决于加在生物学教学上一个数学应用的启蒙观点。真如现在大多数纯生物学和应用生物学的毕业生懂得一些统计方法,并看些经典的模型数学公式化——微分方程系统和马尔柯夫链概率公式——作为实验发现的最后应用。他们并没有涉及数学模型的构造的、判断的,甚至经验解法的真谛。至少,从数学家的观点,似乎有理由开始期望在生物学教学中设立像在工程学教学中所要求的那样多的数学。
另一方面,数学家将如何学习生物学呢?目前,有可能如廿年前处理流体力学和固体力学的同样方法开始处理生物学问题。气体动力学、塑性、行波指导和其它类似问题的数学方面,给那些数学训练已经相当好的人们作为毕业课程,建立更多的研究机会,使应用数学的毕业生花一年或二年的时间在医学和生物学的学习上,并和专门领域的人们一起工作将是有益的。
因此,有理由提倡给数学家以生物学,给生物学家以数学,在教学和未来的研究工作两方面均如此。按我们的意见,较为公正地说,做生物数学家的第二方式的过去经验还未证明是成功的。