(上海师大)
J. M. 凯恩斯是一位著名的经济学家,1911年,年仅28岁就当上了《经济杂志》的编辑,两年之后他又担任了英国皇家经济学会的秘书,但是他仍不间断地为《经济杂志》审定稿子。此后他先后两次在财政部任职,1946年的复活节,即在他与世长辞前的12个月前,被选为皇家经济学会的会长。
在担任编辑与秘书双重职务的时候,凯恩斯在经济学会中起了极为重要的作用,他写下了大量的经济方面的著作,单是公开发行的论著,汇集起来就有8卷之多,再加上他的论文、小册子和重要的信件,以及未发表过的文章、资料、社会活动的报道,还有论及社会政治和文学写作,总共达25卷之巨,这是凯恩斯给人类留下的一笔可贵的遗产。然而,凯恩斯全集的第八卷《论概率》却不是一本经济著作,而是一本论述逻辑命题与概率两者之间关系的论著。
凯恩斯于1906年在印度办事处工作时,已开始研究概率,并在此之后的五年中付出了辛勤的劳动,终于有了一个雏形。但在1911年之后,由于担任了编辑工作,耽误了《论概率》的进一步加工。1914年之后,凯恩斯又重新开始这项工作,终于在1921年8月正式出版,成为英国逻辑概率思想建立五十五年以来第一部系统性的著作,这一本不同凡响的论著,成了卡尔纳普归纳逻辑理论的先驱。
《论概率》—书,主要由五个部分组成:1. 基本概念,2. 基础理论,3. 归纳与类推,4. 概率在哲学上的一些应用,5. 统计推断的基础。限于篇幅,只能作一点扼要的介绍,最后试作一点简单的评论。
凯恩斯认为知识可以分为两部分,一部分是由我们用各种方法直接获得的,即直接知识,而另一部分是要依靠论证而得到的,即间接知识。概率论则与由论证可获得的知识有关。在大部分理论学科中,应用的逻辑都是演绎法,目的都在于论证某种结果的必然性,因而,要求是十分明确的。但是,在其余更多的科学领域里,并不要求这种必然性,而是要求某种程度的合理性。不论在哲学里,或者在其它科学里,大部分的论证,人们都习惯于阐明某种合理的信念,当然,它们在量度上的大小是不确定的,正因为如此,它们需要概率理论。
当然,从历史的角度看,一般地说,沿着逻辑方法所获得的成功,总排斥那种带有不确定性的论证。但是,在实际的推论应用中,我们常常并不期待那种必然性。因此,凯恩斯认为,逻辑研究有效思考的一般原则,应该把论证的重要性放在合理性上。
众所周知,所有的命题或者是真的,或者是假的,扩大地看,也可以是“可能的”。凯恩斯用术语“必然的”和“可能的”来描述一个命题,或者两个命题之间的特殊的知识联系,这种千变万化的联系,可以用合理信度来刻划,而这些合理信度也可以由于命题的变化而变化。
凯恩斯主张,在某个范围里,概率可以看作是主观的,然而,在重要的逻辑意义上,概率又不是主观的。所谓主观,并非是人的任性,因为这样的命题是不可能有的。一旦论据是给予确定的知识,概率所固有的客观性,理所当然地独立于我们的意志。
凯恩斯把直接知识所组成的主体,看作是最终的前提,这个理论告诉我们,由直接知识有根据地论证,都可以得到合理的信念,它们可以是必然的或者是可能的。直接知识命题与我们正在寻找的间接知识命题之间含有纯逻辑的推理。
鉴于上述分析,凯恩斯提出了一个“概率关系”的概念。假设任一命题集合组成前提h,任一命题集合组成结论a,若由知识h证实a的合理信度为a,我们称a和h两者之间的“概率关系”的量度为a,记作a∣h=a。在普通的语言中,我们常称结论是不确定的、靠不住的或者是可能的。然而,严格地说,应该应用术语:在结论中的合理信度,即两个命题集合之间的关系或者论证,将提供与知识相应的合理信度。
概率论的作者们,普遍地运用术语“事件”、“事件的发生”以及“事件发生的概率”。凯恩斯在初次的研讨中,也不离开大家共同的习惯,这样的表达对于逻辑而言,在某种程度上有不明确和含糊之处,因而,将要作一些语言表达上的改进。凯恩斯以“真”和“命题”的概率来代替“发生”和“事件”的概率。
对于一个科学的概念,要么是真的,至少是“似真”的,要不然,就会招致许多批评。但是在通常的思考与论证中,我们假设某个语句,尽管不能证明它是真理,总还能得出某些信赖的理由。对于证据,虽然不能确实地证明某个结论,那也应该是一个合理的根据。凯恩斯举例说,我们接受达尔文的自然选择理论,是因为达尔文给出了有效的证据。我们相信达尔文的证据和他的结论之间的关系是真的、客观的,因而,我们的信念是纯粹的事实。凯恩斯指出,一种命题集合称之为证据,即假设我们“自己知道的,”对于另一个命题集合,我们称为结论,两个命题集合间的关系是客观性的。
综上所述,概率的定义必须满足由合理信度作概率关系的量度,我们不能依据简单的概念来分析概率关系,需通过逻辑推断和真理、错误的范畴,逻辑概率和已知、未知、合理信念的范畴,建立起新的逻辑关系。
凯恩斯着重指出,某些方法可以使概率具备数量特征,因而我们能够唯一地构造适合某种特殊情况的概率序列。凯恩斯还将概率序列与路线图结合起来,作了非常形象的描述:
(ⅰ)任一概率总处于不可能性和必然性之间的一条路线上。(ⅱ)路线或者序列,由概率量度组成,在某个序列中,任何一对概率之间,未必一定再有概率。(ⅲ)某些概率量度能够位于更多的路线上(即能够属于更多的序列)。(ⅳ)若ABC是一个序列,B介于A、C之间,BCD是一个序列,C介于B、D之间,则ABCD是一个序列,B介于A、D之间。
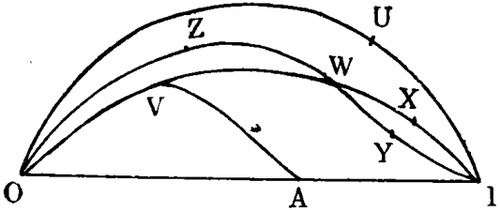
若用0代表不可能性,I代表必然性,A是可用数字表示的可测量的概率,在0和;两者之间,U、V、W、X、Y、Z是非数字概率,从图上可以看出,V比数字概率A较小,也比W、X和Y要小,X和Y比W大,也比V大,但是X和Y不能相互比较,同A也一样不好比较,V和Z比W、X和Y要小,但V和Z也不能相互比较,U与概率V、W、X、Y、Z中任何一个都不能定量比较。全部属于某个序列的概率是可以用数来比较的,这些序列的线称作数线或串,可用OAI来描述。
此外,凯恩斯建立了一些法则,其中最重要的是“无差别法则”。我们知道在相等的概率测定中,要取得普遍的公认,即使对于非等概率测定也是如此。若从数学的角度看,我们必须给予等可能选择的数,以显示等概率法则可以建立。这一法则是概率论的奠基者J · 贝努里在一篇题为《非充分推理法则》的论文中引进,以后被广泛地采用直到如今。但是,凯恩斯认为这种说明并不令人满意,假如能够离开传统的惯例,凯恩斯更愿意称之为“无差别法则”。
“无差别法则”,意指由一些未知的原因来判定某个问题的属性,可以作不同的选择,而与此相关的知识表明,对任何一个选择都是等概率的,因此,必须是对每一个不同的论证以等概率分配,原因很简单:缺乏实在的根据,可以给论证以不等概率的分配。
在充分论述自己的主张之后,凯恩斯开始建立概率关系的公理体系。他用小写字母表示命题,大写字母表示关系。命题、析取、合取都与普通的用法一致。凯恩斯以6个公理14个定义,推导了58个定理,从而建立了他的概率推理的基本理论,使人耳目一新。
逐一介绍固然不可能,看几个凯恩斯觉得颇为有趣的几个定理,不会毫无补益。
凯恩斯将概率与逻辑结合起来,按此来处理合理的论证。当然,这种论证是建立在归纳与类推方法的基础上,几乎所有的经验科学都如此。凯恩斯坚信,归纳过程已经成为始终有生命力的,习惯的心理方法的一部分,归纳过程已慢慢地取得其应有的地位。可又找不到一个满意的叙述。
那么,什么是归纳论证的特征识别呢?什么性质提供了归纳论证的强度?基于什么背景,我们可以把归纳论证看作是合理的呢?
没有什么东西再比鸡蛋与鸡蛋那样类似了,在长期的相同的试验之后,我们能够期望:所有的鸡蛋味道都是一样的,这个论证部分基于类推、部分基于“纯归纳”。在归纳条件里,我们把实例的非本质特征变化的原理称作负类推。论证过后,试验次数的增加,对如下情况是有价值的,通过增加各种各样非本质特征实例的发现,加强了负类推。
从经验论证引起的归纳当中,我们要鉴别两种独立的类型,第一种类型是“普遍归纳”,虽然这种归纳本身对任何一个概率量度都较敏感,但是它们有着固定不变的关系,如果有一个例外发现的话,就被推翻。这些,反之对于精密科学来说,才置目标于建立普遍归纳,而在大多数情况下,我们致力于有更多关联的法则,即第二种类型:“相关归纳”。举例说,这只、那只、…天鹅都是白色的,结论是所有的天鹅都是白色的,我们便建立了一个普遍归纳。如果,这些、那些天鹅是白色的,却有一只天鹅是黑色的,那么,结论是大多数天鹅是白色的,或者天鹅是白色的概率如此这般,这样,我们就建立了一个相关归纳。基于凯恩斯致力于统计推断理论,他就尽可能地论述相关归纳的逻辑基础。
在归纳方法与概率之间的基本关系必须给予强调。我们应该认识到,通过归纳论证所得到的结论是可能的,当然也是不确定的。虽然有些科学家尽力通过逆概率原理来论证归纳过程,拉普拉斯也专门研究过基本的归纳问题,但是,他们很少能明确地理解,每个归纳的有效度,并不依赖于某个结果,而是依赖于概率关系的存在,归纳论证并不断言某种结果一定如此,而是具有一个有利“一定证据关系”的概率。所以凯恩斯主张,归纳有效度和合理的本质是一个逻辑问题,而不是经验的,或是形而上学的问题,也不是物理原理的问题,从感官认识的现实世界决定了证据的特征,而不能决定所给的证据合理地支持什么样的结论。
《论概率》的问世,正值经验主义传统的时代,它使许多哲学家们重新感到,间接知识可以由直接知识通过一种逻辑关系(将概率关系包括在内)而获得一种合理的信念。此书受到当时哲学家的热烈欢迎,原因是凯恩斯的概率观点,填补了当时认识论上的一大空白。
凯恩斯的主要论点是:概率陈述命题a和命题h之间的逻辑关系,人们已知h且发现a和h之间的逻辑关系,那么,有理由认为,在符合逻辑关系的信度中证实a。若这种逻辑关系为:a是h的逻辑结论,则a一定被证实;若虚假的a是h的逻辑结论,则a—定被否定;若以上情况都不是,它是在确实与虚假之间,那么a有部分信度的证实。
凯恩斯探讨问题的独创性在于:他坚持概率从广义上讲,是相关的两个命题之间的逻辑关系。马克斯 · 布兰克(Max Black)在《哲学百科全书》中,有关概率的权威性文章,把这个论点描述为是对“概率”这个名词的“逻辑性解释”,是凯恩斯“针对其对手有力的防御性的逻辑探讨”,它是凯恩斯概率理论的本质所在。
《论概率》写作的时代,正是数学家们在寻找任何领域都会有令人满意的公理体系的时代,凯恩斯对此也作了认真的尝试。他那详尽的理论与方法,虽然如今不再继用,尽管凯恩斯的公理方法还称不上真正的公理体系,然而,他的精华已为后人所继承,在推进归纳逻辑与概率理论的结合上,作出了历史性的贡献,是现代归纳逻辑的一位“开路先锋”。
正因为《论概率》对于概率逻辑带有开创性的意义,那么,它也不可避免地存在着重大的缺陷。首先,凯恩斯主张大多数概率关系是不可测定的,而且,许多对概率关系不可比较,因此凯恩斯断言:并非所有的概率都能安排在0与1之间的某一个量度上面。凯恩斯这一论点,没有得到大部分逻辑学家与概率论学者的赞同,大多数人坚信,每个概率关系都可用0与1之间的某个数来度量。凯恩斯的观点,给自己建立起来的体系,带来了无法弥补的棘手的难题。
其次,凯恩斯理论中颇受挑战的是“概率”的逻辑解释,原因是当时在统计学家中流行的都是“频率理论”。凯恩斯认为,频率可以提供部分的逻辑信息,而不能解释合理信念范围内“概率”的观念,要将频率理论合并到概率逻辑理论中去,还存在着不可逾越的障碍。“概率”的逻辑解释并不能包揽所有的领域,“概率”的频率解释不时地应用于自然科学、社会科学方面的经验理论。在逻辑上解释概率是“确证度”、“可信度”、“可接受性”,而在频率上解释概率是“长程频率”、“统计概率”、“机会”等等。有趣的是这两种解释有时竟在同一个句子中提到。实际上,贝叶斯学派的先验概率,往往是参照这两种概率综合地给定的。如何更好地处理好这两者关系,成了概率逻辑中的一大难题。
最后,虽然凯恩斯致力于构造两个命题之间逻辑关系的公理体系,但却没有与数理逻辑的形式系统充分挂钩。历史上第一个创建严格的关于逻辑规律的公理系统是逻辑学家弗雷格,虽说他的著作在19世纪末叶已经问世,但由于不便理解而鲜为人知。凯恩斯创作《论概率》,正处于数理逻辑脱颖而出却又未成熟的时期,因而,这一缺陷也是历史的必然。凯恩斯的《论概率》拟是概率理论运用于两个命题间的逻辑关系,尽管也有一些创新的表达形式,可是,由于繁杂而不可能为逻辑学家们广为采用。卡尔纳普的新的归纳逻辑理论的产生也就势在必然了。
归纳理论的地位的辩论是从休谟开始的,凯恩斯的理论是一个新的转折。这场辩论引起了哲学家、逻辑学家、数学家以至其他科学家们的极大关注,不管历史的进程如何曲折,凯恩斯的《论概率》总是归纳理论发展的一个重要的丰碑。