人们已经创立了很多有价值的成像方法。本文介绍的是对不规则的自然系统成像的研究,而不是那些非常特殊、非常简单系统——例如透镜和球面镜——成像的研究。
下雨的夜晚,如果你透过眼镜或窗格玻璃上的水迹去观察路灯,这时,所看到的影像会令你感到吃惊。光线透过有细微波浪的水面照射到水中时,水池或水槽底部就会出现一种紊乱的明亮线条组成的网状图形。为进一步认识、解释这些不规则的影像与图形,我们必须在经典光学的基础上增补灾变理论——这样,就产生了灾变光学。
不规则系统成像,在遥感(例如雷达、声纳及地震等)领域里的应用非常重要。在这方面,灾变光学的任务是设法找出形成已知波场的原因。在某些情况下,人们还能通过影像的灾变形态认识散射的本质特征。另外,图形的变也处理也是以这个观点为根据的。例如:地震工作者早已知道,岩石层沟槽部位(向斜结构)所形成的地震波曲线,看上去有点像图2中那种通过燕尾形面的截面。已有人对这些图形的一般关系进行过分类,不过,当前这方面尚需进一步开发。灾变光学还应用于发光研究及波通过小孔以后,形成偏离直线前进的/h范围散射方面的研究。
“灾变理论”这个名词是数学家克利斯朵夫 · 齐曼(Christopher Zeeman)推广法国拓扑学家雷纳 · 托姆(Rene Thom)建立的纯粹数学时创造的。托姆当时使用这个名词与不均匀,不连续及突变有关,该理论还能描述它们。最早正确评价灾变理论的物理学家有米歇尔 · 贝里(Michael Berry)和约翰 · 奈(John Nye)他们详细介绍了大量可靠的灾变光学理论及实验方面的研究工作。“灾变光学”这一名词则首先出现于一篇评论性文章的题目中。
成像、调焦和焦散
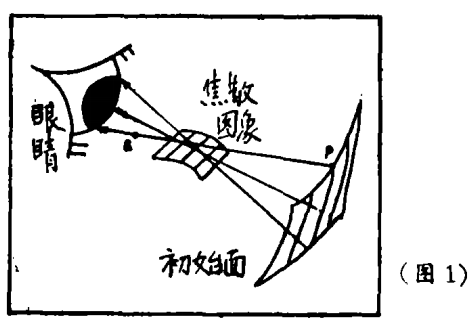
每一幅光学图像都是光线经过光学系统调焦和聚焦以后产生的,只要在机械加工方面仍存在缺陷,实际上的精确点聚焦就不可能存在,光线经过任何实际系统聚焦以后,最低限度会形成一个明亮的面(图1)。我们之所以称这一情况为焦散,是因为这时光线通过光学系统以后仍然得到了一个残像或光斑,雨夜中看到的奇怪影像及水池底出现的明亮网纹都是光线通过聚焦面后形成的截面图。
我们应该怎样认识并解释上述那些表面看上去很不规则的图像呢?利用灾变理论就能一部分、一部分(局部)地认识它们、并解释它们。剩下的难题就是想办法怎样把这许多的小部分联系起来,使之成为有机整体。不过在这以后灾变理论和光度学理论对我们可能仍很有用。
基本灾变和光学
灾变理论能具体应用到一般系统上,并具有跟大多数应用数学不同的独特方法,所以它非常有用。另外它还有点像统计理论,忽略少数特殊情况,以有利于对一般情况的研究。基于这些原因,我们认为以前灾变理论是不可想象,而且也是不可能出现的。
托姆的一个重要观点就是把灾变理论看成是动力学系统理论。一个特殊情况是设想这些系统在不断运动,以便于求其某一位形函数的极小值(或更一般地说,是不变值)。例如,让一个向平衡位置运动的动力学系统突然停止,从而求其势能函数的极小值。适用于这类动力学系统的灾变理论,通常人们称它为基本灾变理论。
几何光学为一基本动力学系统。根据弗马原理可知,光线沿光程不变的路线(通常是极小值)前进。简单光学系统所包含的各部分性质相同。在这里光线可以分别处理,并且都是直线传播的。在上述区域内,光线的形状可以表示为两点一位置在确定平面上的P点和已知的Q点之间的直线。
P点可以用两个(曲线)坐标(x、y)确定,而Q点则需要用3个坐标(u、v、W)表示。该系统也可以用别的反映介质性质和表面形状的参数描述。在必要的情况下,它们还能用别的变量a、b、c…表示。如果使用本学科的术语,(x、y)可称为态变量,因为它们能确定一个系统的本征态。而(u、v、w、a、b、c…)则称为控制变量,因为这些变量能够控制系统的状态。
已知光程函数p(x、y:u、v、w、a、b、c…)所确定的光线路程相对于z、y是不变的。如果有退化解或多重解出现,意味着这时有两条(或更多的)光线已经聚合在一起(即聚束),因此焦散面由上述条件确定。如控制变量多于三个以上,我们就可把焦散面看成是二维控制子空间的一个表面(通常实际观察值空间包含Q点),这时焦散面的形状取决于余下的控制变量。
焦散面模型
基本灾变理论为我们提供的是简单的局域性焦散面模型,这些模型通常出现在普通系统中。这些模型对于函数φ是多项式并通过坐标的光滑变换与φ相联系,这样的联系使客体具有保持优势的特点。例如任何多边形都有可能保持其角度不变,尽管有时它们的角度会发生变化,而且有时边也会发生弯曲,不过在椭圆的圆周上绝对不可能遇到拐角。简单的局域性焦散面模型还能为我们的研究提供令人满意的数学方法,以致使那些有用的定理有可能被证明。
目前灾变理论更深远的影响还不十分清楚,灾变模型的数量受态变量及控制变量数量的限制和约束。托姆曾经提出过一个多达四个控制变量的类型。假如想把控制变量空间表示为时 - 空四维空间,托姆所提出的这一类型是足够的。在这种情况下,对于任何数量的态变量来说,标准模型的数目都不会多于7个以上(它在生物学方面有重要应用,例如,可以用态变量去解释有机物蓄电池的化学势)。
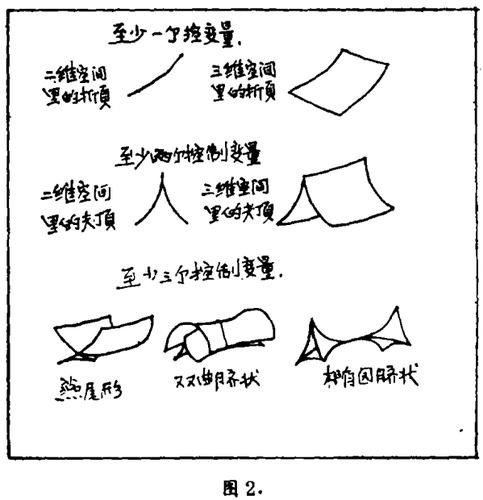
灾变光学一般只包含两个态变量。这样,三个控制变量就有5种标准焦散模型。通常在控制变量的维数出现最小值时,焦散面就会像稿纸那样并列地排在一起。正像我们在图2中所看到的那样,分别为两个尖顶的,或折叠在一起的焦散面。另外焦散面还能跟别的焦散面相交。因此已知的各种简单焦散面可以构成更复杂的焦散面结构(但需要借助于某种约束和限制,来维持它的特征和稳定性)。
构造核
灾变模型具有一定的层次结构、因此任何一个灾变模型构成另外的灾变模型时只需要较少的控制变量。这可以从图2中看出,三维尖顶形焦散面包括两片沿锐利尖棱粘在一起(折叠)的焦散面,所以尖顶形焦散面可以看成是两片相互联接的折叠焦散面构成的。三个以上控制变量的灾变模型虽然已经建立,但是通常已无法直接看到。它们通常被看作为次要灾变模型。
那些明亮的“变形虫”似的图形都以曲线为其边界。它们一面明亮而另一面较暗,这是因为亮的一面光线至少要比另一面多一倍。从图1可以看出通过焦散面上任何一点都有两束相交的光线(图上看到的是3束相交光线),而在另一面却一束光线也没有。如果我们假定它是一维图形,那么灾变光学就能预先告诉人们,任何一种焦散面,或者只包含有一片光滑的(折叠)焦散面;或者包含有几片连接在一起的光滑焦散面,这样的焦散面也有可能相交。
不过,我们已注意到三棱焦散面是由两个三角形尖顶及一个交叉点构成的。上述复杂图形中较大的部分看上去很像是通过燕尾形面尾部的截面图(见图2)。这一切使人联想到上述各种焦散面的某些部分是由燕尾形的灾变模型构成的。假如有可能再发现一些新控制变量,人们也许就可能观察到所有各种燕尾形焦散面。然而实际上已经证明,这样做是相当困难的。不管怎样,只要调节好显微镜的焦距变化,我们在其水滴形透镜的近场中,就能顺利而且清楚地看到有三个控制变量的三维椭圆的或双曲线的脐状焦散面。先测出灾变模型的特征截面,然后设法寻找它的支点。这是灾变光学的一般研究内容。
引人注意的部分是衍射条纹,它们十分明显接近灾变图像的边界。通常人们都是用激光来拍摄这种具有衍射条纹照片的,不过,一般地说,要想得到衍射条纹照片,用街灯灯光,在单色性方面已能满足条件了。这些衍射条纹也能用灾变理论加以说明。
衍射灾变
衍射的数学模型使人们可以用光程长度正弦函数φ的积分和波长描述波函数。建立灾变模型的方法是用多项式模型替代φ,这时波长基本上被取消,因而形成了衍射灾变。实现波长取消这种变量变化以后,人们就能确定衍射图样的亮度与宽度是如何随波长变化的了。
对光程长度正弦函数φ可以积分说明对标准衍射灾变能进行数值计算。约翰 · 奈使用精心调整好形态的微小水滴做了许多衍射灾变方面的实验研究。有人做了实验与理论的比较工作,曾取得令人意想不到的好效果,尽管在简单直接类比中,所有的近似方法都是没有疑问的。
普遍存在的Xg
托姆提出的类型经过俄国数学家V. 阿诺德(Arnold)发展后,控制变量的数目已远远超过4个。他曾发现了很多新控制变量(一般说来光学中仅只多于5个,但是如果有两个态变量,其控制变量的数目就会多于6个)。被人称为形式变量的多余参数非常复杂。
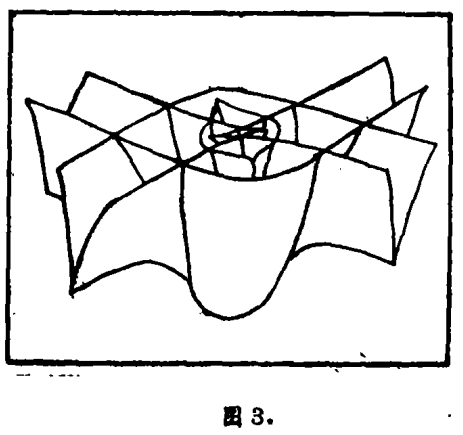
形式灾变并不是一种很难理解的数学古玩,它们是通过对有细微波浪的水面,微小的水滴及实际的“经典”“理想”透镜调焦后建立的。阿诺德系统的基本术语中,最简单最重要的称为Xg,它有7个控制变量和1个形式变量。为数众多的三维聚焦面中的任何一个都是图2中看来像两个相交的尖顶面Xg构成的。不过事实上,它并不简单,即使改变参数也不能使退化上升,因此无法揭示出现在图3中的焦散面结构,以增进人们对Xg的复杂性及美观的了解。
水波光学
水面波浪的作用很像柱面透镜,它能够把光线聚焦到尖顶形的焦散面上,但是普通光源的非准直性和水波的运动,都会使焦散面变模糊,以致两片焦散面消失,这样焦散光线便投射到水底而呈现蜿蜒前进的宽明亮条纹,通常水面上的波纹是同时向各方向传播的,由于焦散光线的相互交叉,最后就形成了一张生机勃勃的,蜿蜒曲折的网纹。不过,人们不禁会问这些焦散光线为什么发生交叉呢?
两个或更多的綑微波纹的波峰重叠处,将形成一个半球形折射面。它的聚焦点由Xg调节。Xg在水底形成的交叉焦散面看上去有点像图(3)中的尖顶焦散面截面。因此可认为它是两条焦散光线的简单交叉,尽管事实上可能非常复杂。不过它能使正常光源变得模糊不清,像个“瘤状物”。经频闪仪(使用时应避免移动)或平行光源(使用时要避免倾斜)照射的波纹玻璃折射透镜,或别的波纹容器还能得到更复杂的焦散面的组合。
光学畸变和球体光学
光学的大部分内容与旋转对称系统的成像有关,这种对称发生破缺时(光源离开主轴即出现),它们将会变得难以描述。这恰好是一种破坏光学系统设计工作者引以为奋斗目标的理想成像方法。所有这样的异常都称为畸变。灾变光学提供的就是一个由Xg构成的畸变体系。
大多数透镜的畸变是球形畸变。光线在焦点到透镜的距离之外通过透镜就会出现这样的畸变。这种畸变把“理想的”点聚焦变成“尖顶圆锥”再加上圆锥顶中一根轴线聚焦。旋转对称的焦散面恰好在用Xg灾变描述的参数范围之外,不过只要旋转对称稍微出现破缺,Xg就会替代轴线,并“迅速发展”成为一个四只环绕它,并向外指的尖顶细圆柱,而在原来焦点附近,该圆柱和它外面的光滑尖顶圆锥筒的结构很像图3中的那个焦散面。
使旋转对称破缺的另一个办法是把透镜压扁。例如,对于具有强烈破坏性地震产生的地震波来说,地球本身就是一个椭圆形或压扁了的球状透镜。这时地震波将被聚焦于地面断裂形成的焦散面上。人们很想用—种类似的焦散面来描述地震波的焦散面。有迹象表明。有一部分地震波焦散面确实是有4个小尖孔,其四周包围着许多更大的孔,然而在更大的尺度上其它恒星的光经过火星这种行星的球形大气折射以后,也会形成类似的焦散面。某些由此形成的有四个尖顶的焦散面,已被人们观察到。
传统的光学仪器制造商们一直认为部分衍射图案与透镜畸变有关,他们称这样的衍射为慧差。它实际上是由于光源被放置在离开主轴一些距离时旋转对称
发生破缺引起的。灾变光学仪器制造商们则认为它是由Xg构成的(异常)双曲脐状衍射灾变。图3可以看出,双曲脐状衍射灾变的确是由Xg构成的。焦散面的主体有四条尖棱,每条尖棱都指向光滑弯曲面,这正是双曲脐状焦散面的特征外形。彩虹是人们最常见的由微小水滴的焦散面形成的,不过球状水珠受到重力作用变偏后,也有可能把焦点集中到慧差双曲脐状焦散面上。
定量应用
灾变理论主要用¥描述,并预言光学上不规则自然系统及受干扰的规则系统中所出现的焦散面形状,但它并不是定量理论。例如,星光的闪烁就是一种不规则的聚焦现象。Michael Berry曾根据灾变光学理论对星光闪烁的次数进行过详细统计,这一统计还受到透过有细微波浪水面照射的激光实验的检验。
我们还有可能获得焦散面几何图形的精确数据,并根据灾变理论去考虑它的应用。我个人目前的兴趣是开发计算机的代数系统,以识别灾变模型,建立与其生成函数光滑坐标变换有关的恰当多项式模型。
[Physics Bulletin91988年第8期]