图论是研究 “图”的性质、结构、运算和应用的一个数学分支，起始于欧拉对“七桥问题”的解答。目前发展迅速，在物理、化学、生物、心理学、经济学、语言学等学科开始扎根。本文试图以简练的笔法，准确地陈述图论中的基本概念、方法，以及在车辆运输、信件投递、婚姻匹配、地图着色等方面的应用。

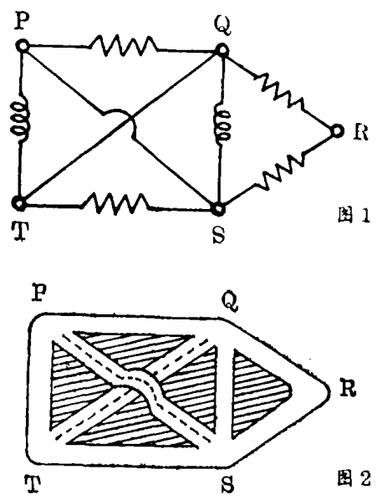
我们首先考虑图1和2，它们分别表示一个电路图和一个道路图，显然它们都可以用由点及直线组成的图3来表示。点P、Q、R、S、T叫做顶点，线段叫做边，整个图形叫做图。（注意，进线PS和QT的交叉点不是图的顶点，因为这两条线路或道路并不相交。）顶点的度是以该顶点作为端点的边的数目，在图2中表示交叉路的数，因此顶点Q的度是4。

显然图3还可以表示其它情况，例如，如果P、Q、R、S、T表示足球队，则边可以表示端点所表示的队之间的比赛关系，（因此在图3中P对S比赛但不对R比赛）这种情况，顶点的度数表示队际比赛的次数。

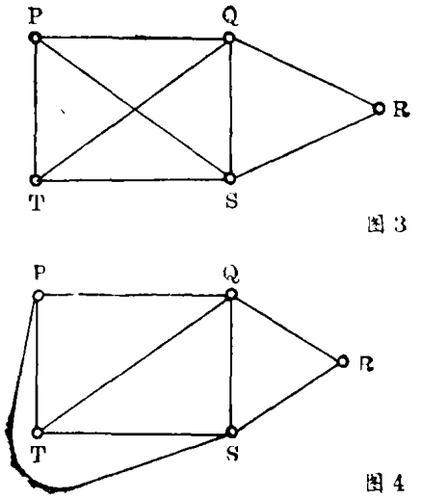
描述上述情况的另一方法还可用图4给出。这里我们把与线段TQ交叉的线段PS移到了四边形PQST的外面。注意，图4仍然能告诉我们原来的电路图是怎样连接的。不论从一个交叉点到另一个交叉点是否有一条直接的路，也不论哪一个队与哪一个队是否钉比赛。我们所丢掉的信息只与“度量”性质有关（路的长度、导线的曲直等等）。

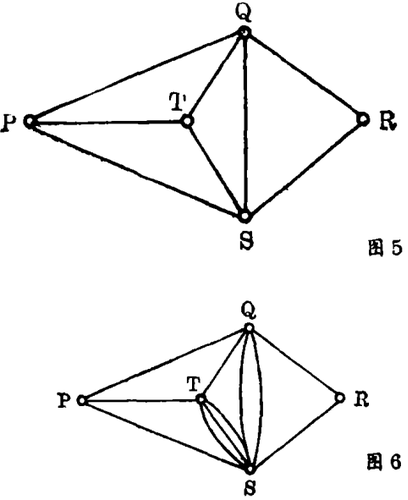
我们试图说明的一点是，一个图表示的是一个点集和连接它们而成的路，它们的任何度量性质与我们所要研究的问题无关。按照这一观点，表示同一情况的任何两个图（如图3和图4）应视为同一图。更精确地，我们说两个图是同构的，如果它们的顶点之间存在一一对应的关系，这些顶点有这样的性质：两顶点在—个图中用一条边相连，当且仅当它们对应顶点在另一个图中也有一条边相连。另外，同构于图3和4的图还可以用图5表示，在这个图中所有空间和距离的概念完全消失，然而哪些点是被线或路连接起来的，仍然一目了然。

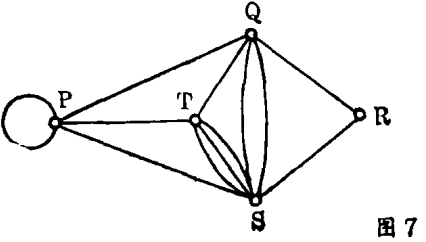
值得指出的是，至今我们已经讨论的图是特别“简单的”图，即在给出的一对点之间至多有一条路。现&我们假设在图5中连接Q和S及S和T的路上的运输量非常大，那么这种情况可以用建立另外的连接这驻点之间的路来缓和，其结果如图6所示。（连接Q和S或S和T的边叫做多重边。）如果我们希望另外在 p处建立一个汽车场，则可以在图上用画一条p到p的边来表示，通常叫做环（见图7）。一个图通常包含环和多重边，不包含环和多重边的图（如图5）称为简单图。

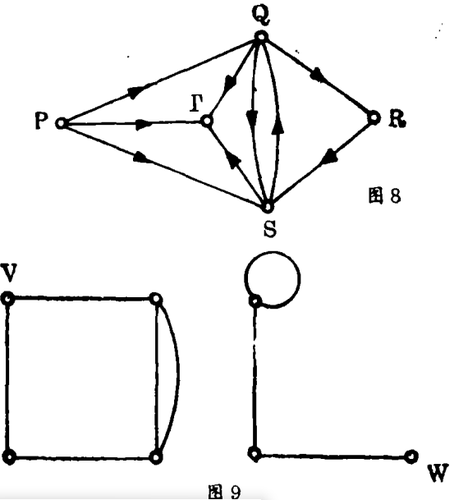
有向图的研究是起源于“如果所有的路都是单行道将会发生什么？”这一问题。例如图8，单行道的方向用箭头表示。（在这个例子中，在T完全是无秩序的，但并不影响我们研究这种情况！）如果不是所有的街道都是单行道，那么我们可以用两条单行道代替一条双行道，从而获得有向图。

图论包括对各类通路的研究，一条通路本质上是一条边后接另一条边的序列。例如在图5中P→Q→R是“一条由P到R的路”，且它是长度为2的通路，类似地P→S→Q→T→S→R是一条长度为5的通路。显然形如Q→S→T→Q的通路叫做一个圈。

—般地，在图中给出两个顶点V和W，并不一定都能找到连接这两个顶点的通路（见图9），只有当图是“连成一片”时这样的通路才存在。显然，我们可以认为图的顶点是伦敦和纽约的地下铁道的车站，它的边是连接这些车站的直线，而不可能用图的边从伦敦特拉法尔加广场到纽约宏大的中央车站连接起来。另一方面，如果我们限制在伦敦地下铁道的车站和线路，那么我们可以从任何一个车站到另一个车站。任意两个顶点都有一条通路的图叫做连通图。

讨论只有特殊性质的道路构成的图是有意义的。例如包含通路的图，而通路包含每条边或每个顶点仅一次，终点在起点，这样的图分别叫做欧拉图和哈密尔顿图。例如图5是哈密尔顿图（一条通路是P→Q→R→S→T→P），但它绝不是欧拉图，因为任一条包含每条边仅一次的通路（如P→Q→T→P→S→R→Q→S→T），它的终点必不同于起点。

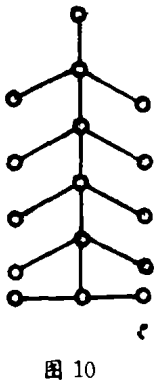
每两个顶点只有一条通路的连通图，这种图叫做树（推广到家族树的概念）。我们将看到树可以定义为没有圈的连通图（见图10）。

稍微偏离一下我们讨论的问题，读者可以回忆一下，当我们讨论图3时曾指出有许多图（如图4和图5）与其同构，而且这些同构图不含有交叉点。用这种方法画出的没有交叉点的任何图叫做平面图，这样的图在图论中是极为重要的。刻划平面性有几个标准，其中有些包含图的子图的性质，而另一些包含对偶性的基本概念。

平面图在着色问题中起着重要的作用，为了解决这些问题，让我们回到“道路图”，假设Shell. Esso、Betz和Gulf想要在P、Q、R、S和T处建五个汽修厂，进一步假设出于经济上的原因，任何一家公司都不愿将自己的两个汽修厂建在两个相邻的路口处。则一种解法是Shell建在P处，Esso建在Q处，Betz在S，Gulf在T处，剩下的将是Shell或Gulf再在R处建一个，不过，如果Gulf决定不遵守此规定，那么其它三个公司显然无法按这一特定方式建厂。

这个问题可以变换成用K种颜色对一给定的简单图的顶点着色问题，它要求图的每一条边有不同颜色的端点，如果恰是平面图，我们将看到只用五种颜色就能按上面提到的方法对图的顶点着色，而且最近已经证明只用四种颜色就能完成此任务，这就是著名的四色定理。（这一定理的另一较熟悉的方法是，用四种颜色在地图上着色，就能使得地图上任意两个相邻国家具有不同的颜色。）

图论还研究各种匹配问题，包括著名的婚姻问题。问在什么条件下，一个男子的集合（他们中每人都认识几个女孩）中的每一个男子能与他认识的一个女子结婚。这个问题可用断集的理论来表示、断集理论是匹配数学的一个重要分支。其结果是这些议题与这样一个问题密切联系着，即在任意两条通路不能有公共边的限制下，找出图或有向图中连接两个给定顶点通路的条数。

对网络流及运输问题的讨论。为了说明这些问题，我们假设图5表示由不同材料的导线组成的电网络，问题是要求出多大的电流能安全地通过从P到R的整个电路，对于不同的电流，每一根单独的导线都不被烧断。或者，我们把P作为工厂，R作为市场，图的边作为能很好发送货物的各种路线。在这种情况中，若给定了各条路线的容量，我们要知道有多少货物可以从工厂运到市场。

用拟阵理论将把以前的内容串起来以达到最佳。事实上，拟阵论本质上是研究具有“独立结构”的集合，不仅推广了向量空间中线性相关的性质，而且还推广了本书前面得到的一些图论的结果。然而，我们将看到，拟阵论绝不是“为了推广而推广”，相反地，它给我们对某些图论的问题以更深刻的理解，同时还包括了断集论的一些结论的简单证明的应用，这些证明用传统的方法是很难的。我们相信，在未来几年中，拟阵论在匹配理论的发展中将起到重要的作用。

[Introduction to Graph Theory第2版］