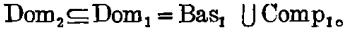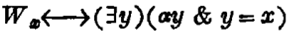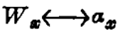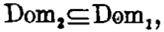1

我们的学术界普遍注意到西方科学哲学从所谓逻辑主义向历史主义的演变，然而这仅仅是西方科学哲学变化的一个方向，或确切点说，它只是众多方向之一。事实上，逻辑经验主义自三十年代所倡导的统一科学运动，历经几十年，至今仍在继续发展。

早在1972年，美国德克萨斯大学的考西（R. L. Causey）教授在《实体属性的微化》以及《一致微化》这两篇论文中，为统一科学的微化方案奠定了基础；1976年又发表了《实体和微化：一个答复》；1977年则出版了《统一科学》—书，系统地阐述了他的统一科学纲领。由于考西的工作，统一科学步入了一个新的阶段，因此他的观点在欧美学术界引起很大反响。1980年密歇根大学的斯克拉（L. Sklar）在《科学哲学》第4期上专门为考西的《统一科学》作了评价。当然，人们对于他的微化方案看法并不一致，但无论是赞同或反对其主要根据都集中在微化方法上。例如，持反对意见的印第安纳中心大学的麦克考莱（R. N. McCauley）1981年著文《假设的本体和本体的简化：评考西的统一科学方案》批评微化主义；而受到启发的科学家们则把微化方法推广到科学领域之中，如M. Ruse借用微化方法提出《发生学中的微化主义》。

鉴于微化方法在考西统一科学方案中的重要作用，本文拟就微化方法作些讨论，以探明考西统一科学的机制。

2

虽说考西被叫作“微化主义”，但微化方法并不是他第一次提出的。在考西之前，人们就曾经提出过“化归”这个概念：

两种科学理论T₁与T₂，当T₂的规律被T₁解释了，并且这个解释满足某些条件时，就说T₂化归或还原为T₁。

在此基础上，人们又区别出一种特殊情况，即

当T₁与T₂的域重叠时，这种化归就叫所谓“微化”。

而考西则不同，他在更严格的意义上用集合论的语言刻画了这一传统观念并使它有了新的意义。

从T₂到T₁的微化的基本必要条件：把T₂化归为T₁，其中Dom₂的元素与Dem₁的某种元素相等。并且，假设Dem₁常包含着在T₁看来没有构成整体的基本元素的子集；假设Dem₁可以包含其部分是由基本元素构成为整体的复合元素。这就是说，Dom₂中的元素既可以与Dem₁中的基本元素相等，也可以与其复合元素相等。

微化只有在这种条件下才可能进行。例如把热力学化归为统计力学，把光的波动理论化归为电磁理论，把化学化归为原子 - 分子论、把生物学化归为化学和物理学，把社会学化归为个体心理学等等都属于这种微化。

古典宏观化学涉及到给种种物质分类并探索描述其属性和转化（反应）的规律，原子 - 分子论就是为了提供其微观的解释而发明的，而物质不能被无限分割无疑是一个经验事实，因为在经验上各种物质都存在着最小颗粒。古典化学仅仅与物质在经验上的最小颗粒（ESS）有关。我们假设理论Ts是概括实体（ESS）的领域的，且该理论Ts应用一组原始非逻辑谓词&s。&s可分为两种，一为实体谓词，一为属性谓词。前者如金、硝酸等等；后者如沸点=100°C，溶于HCl溶液中。但严格点说，&s的实体谓词并不是物质名词，因为Ts的对象不是一般的物质而是关于ESS的。这些原始的实体谓词皆为均质实体谓词，而Ts所反映的正是有关ESS及其属性的一组规律。

微化的对象是把Ts化归为原子 - 分子论Tam。Tam是应用原始非逻辑谓词集合&am的一种理论。&am中的实体谓词指称原子的种类，如氢原子，金原子，这些都是均质实体谓词，因为所有相同种类的原子具有严格的同一原子的分类属性。一切原子集合的任何种类的原子都由这座原始均质实体谓词来指称或者说它在&am中是可定义的。微化是通过使某类已知在经验上最小颗粒与原子或分子（如“H₂O分子”）相等来进行的。当然，Ts的规律必须由Tam的规律来解释，为达此目的借助于相应的语句集合作适当的解释推导是可能的。

首先，Tam处理两类个体：

（ⅰ）原子，从Tam的观点来看，它是基本个体，因为它们不是由部分构成的；

（ⅱ）分子，它们是复合体，因为它们由两个或多个原子构成。

再者，Tam是这样的理论，其指称原子或分子类的谓词是均质实体谓词，同样地，在Ts中指称某类在经验上最小颗粒的谓词是均质实体谓词。这就是说，当某类在经验上的最小颗粒与某类原子或分子等价时，指称这个在经验上最小颗粒的谓词的均质性是可以理解的，因为指称相应的原子与分子类的谓词的均质性是可理解的。

3

任一非逻辑谓词&_i=g_i∪A_i（i=1,2）,g_i是实体谓词集合，A_i是属性谓词集合。在微化中将使Dom₂与Dom₁中的那类实体相等，使T₂中的属性与T₁中的相等。

为了描述某类构造，人们必须指出两个或多个基本元素的有限集合，并指出已掌握的这些元素之间的某些结构关系。为了使&₁有可能描述结构，就需要A₁有某种结构关系谓词或者有某种谓词在A₁中是可定义的。凭借这些结构关系谓词可以描述复合元素的种种可能结构。例如，在古典化学中，分子结构是借助于有关以种种形式存在的化学键和化合价来描述的。我们说两个基本元素是同类（或同型）的，假如并仅假如它们处于相同的自然等价类中。由于这些自然等价类是由&₁的基本均质实体谓词来指称的，所以这些基本均质实体谓词为基本元素的类称。显然，一切结构都由基本元素作为其部分而构成。Dom₁中的结构的一切部分都是Bas₁的元素，而不是ComP₁的元素。这就是说，我们可以说种种结构都有相同的种类，根本不存在任何结构的结构。上面所举的化学实例就说明了这一点：我们有原子和分子，而原子是分子的部分；任何一个最小的可能颗粒都或者与原子相等或者与分子相等；我们无需考虑其部分是分子的结构的问题。

由于ComP₁具有结构，并完全由同一种类构成，我们可借此阐明一层微化的条件。所谓一层微化，即从部分（基本元素）到整体（复合元素）至多只跃过一个层次，所给出的一层微化条件可以推广到多层次微化中。

在大多数具有整体结构的理论中，有可能出现这种情况，一个给定的基本元素可能在某段时间里没有被组合，而在其他时间与结构中的其他基本元素组合。一个在结构中没有被组合的基本元素处于自由态的，相反与结构中其他元素组合的基本元素是约束态。

假如&₁有适当的谓词描述这些基本元素的可能状态，并且由于这些状态有可能依赖于某种外部的环境条件，&₁也有适当的谓词描述之；关于复合元素的情况亦类同。由两个或两个以上基本元素构成的复合元素C满足由基本实体谓词和相应的属性谓词所定义的构造描述。这里所谓构造描述，指某类有限的基本元素被整理为它们之间的某种已知结构关系。这种结构关系，依据基本属性谓词，必然是可定义的。假如C是复合元素，C的域是由C组成的基本元素的集合。两个复合元素C₁，C₂，是同类（或同型）的，假如并仅假如它们满足一些已给的构造描述。这就是说，C₁，C₂是同类的，假如并仅假如

（ⅰ）在其域中的元素之间有一一对应的关系，它与同类基本元素相关；

（ⅱ）其域中所对应的基本元素以相同的方法在结构上与C₁和C₂相关。

如果Φ₁和Φ₂是两个构造描述，那么或者

E_xtΦ1=E_xtΦ2，

或者

E_xtΦ1∩E_xtΦ2是空集。

而Comp₁的分类就是依据构造描述，并且完全用定义的方式进行的，因此，使复合元素相同或相异的方法只能是结构描述。由此可见，假如Φ₁，Φ₂是任何两个结构描述，那么它们不是在分析上等价就是在分析上无关即不相交。这就意味着：两个复合元素C₁，C₂是同类的，假如并仅假如它们满足分析上等价的结构描述。

假设ψ是&₁所定义的一个二元关系，并且令E，是在Bas₁基础上定义的自然等价关系，那么ψ是定义分类属性谓词，假如并仅假如对于一切基本元素b₁，b₂，b^'₁，b^'₂，若E₁b₁b'₁和E₁b₂b'₂和ψb₁b₂（在特定的条件下），那么ψb'₁b'₂（在特定的条件下）。

可见，如果b是基本的，c是复合的，那么b和c显然分属不同种类，因为它们的类属性不同，根据上述的讨论，我们不难知道：Dom₁中的任何两个元素是同类的，假如并仅假如它们有严格相同的分类属性，考西把它叫作一般同类原则。

现在来看Dom₁和&₁有一域

Dom₁= Bas₁∪Comp₁，

这里Bas₁是非空的，Comp₁在终极微化中也是非空的。在此情况下，&₁有可能定义Comp₁的一切可能种类的复合元素。这些定义是应用构造描述——刻划复合元素的种种结构——来完成的。这些构造描述就是分类属性谓词。另外，其他种类的属性谓词在4中一般是可定义的，其中有些是分类属性谓词，有的不是。而依据一般同类原则，Bas₁被分为基本元素的同类子集，Comp₁则被分为复合元素的同类子集。这些复合元素的同类子集可依据&₁中所确定的种种结构描述的类型来指称。

—个成功的化归需要在其他实体中，提供这些类的一个可理解的同类性质。获得理解的方法是设法使这些类与Dom₁中的同一类相等。换句话说，化归说明了

当然，Dom₂的同一类必须与Dom₁的同一类相等。可见微化包含使Dom₂的某类元素或者与Dom₁的某类基本元素相等，或者与Dom₁的某类复合元素相等。上述所举的化学的例子很清楚地说明了这一点。

4

在考西之前，不少人都曾提出过化归条件，但由于过分依赖于集合论语言，因此，没有把真正的实体和属性相等与规则学对等外延区别开来。例如：

令“W”是&₂的同类实体谓词，即“W”是指Dom₂的同类子集的实体谓词。那么E_xtw的一切元素，除去其非分类属性之外都相同，即E_xtw的任意元素与Dom₁的某类基本的或复合的元素相等。因此我们有联系语句

式中α是&₁中的或被&₁所定义的某种同类实体谓词，即α是Dom₁的一类基本的或复合元素的谓词。上式告诉我们，任何事物x，它是W，这就与有些y是α相等的。由于它是集合，在理论上等价于

这说明E_xtw=E_xtα。像这种形式的联系语句就是所谓实体相等联系语句（TICS），它对于微化是起本质作用的。事实上，由于我们需要

&₂的任何同类实体谓词应化归为&₁的同类实体谓词。

令“A”是不在&₁中的&₂的一元分类属性谓词，且“E”是描述某类环境条件的谓词。E属于&₁和&_2。假设T₂含有基本规律语句

（W_x & E_x）→A_x

那么很显然在T₂的化归过程中，人们必须解释，且仅须解释T₂的基本规律语句。相似地，为完成简化联系语句，除TICS之外，还需要ACCS，即属性相关联系语句。但是，集合论不允许应用属性或指出属性相等这个事实，因为属性相等即同一类，故无所谓彼此的区分。所以一个充分的简化所需要的更强的条件无法用集合论的语言来陈述。

5

我们有用非逻辑谓词集合&₁，&₂来表述的理论T₁，T₂。其中T₁概括Dom₁=Bas₁∪Comp₁的元素。Bas₁是由自然相等关系所分割成的同类子集，而Comp₁是根据这些复合元素的结构而分割成的元素同类子集。Dom₂也由其自然等价关系分割成同类子集。为了避免用暗中假定的实体、属性或规律作简化，语言&₁和理论T₁必须满足所述条件。并且简化包含根据T₁∪B来推导T₂，这里B是联系语句的一个真子集。

令F_i，D_i分别是T_i（t=1，2）的基本的和导出的规律语句的集合。令T₂是借助于有关实体相导和属性相等的集合B而简化为T₁的。为了完成这个简化，T₂的任何规律语句必须由T₁的规律语句加上B中的相等来导出。由于D₂的规律语句在T₂中是可解释的，要从T₁的语句加上B的语句来推导F₂的规律语句才是必要的。通常这些推导都是解释者。

又令f₂∈F₂。f₂的任何一个非逻辑谓词都将被所确定的非逻辑谓词的相等语句所简化。也就是说f₂与L₁为规则学等价，即f₂n-eqL₁，这里L₁是用&₁所表达的规律语句。在大多数情况下，L₁是T₁的可推导规律语句即T₁内有L₁的解释推导。由此可见，在严格的意义上，简化包含下述条件：

F₂的任一规律语句或者是

（ⅰ）根据F₁UB所作的解释推导。

或者是

（ⅱ）借助于B证明与F₁的成员n-eq。

这个化归确实没有增加T₁中的任何新的非T₁规律语句，于是，至少剩下尚需进一步解释的T₁的基本规律语句。

假如α，β两个属性谓词是综合对等外延，那么所谓α与β相等，假如并仅假如这个对等外延是非因果的。若这个对等外延是规律，那么我们有一个规则学对等外延或者一个属性相关规律。考西在属性相关规律语句和属性相等之间建立了区别。以前有人曾注意到这种区别，但认为意义不大，因为已经有了所谓偶然对等外延和规则学（类似规律）对等外延的差别。然而规则学的对等外延不能作为充分简化中的联系语句。例如视觉的能动性和分子不对称性之间的相关性无疑是一个确证的规律，它曾被一些成功的实验所解释。可是它并不是联系语句，并且也不是属性相等。所谓“相等”恰恰是相关规律的极特殊类型，它尤其适合用作化归中的联系语句。为了使这样的特殊的相关用作联系语句，它必须是非因果的。因此它们不是规律。无论如何，这样特殊相关不是T₂与T₁的类及属性相等，所以它们实际上不可能是联系语句。

考西以微化为基础，提出统一科学、他所谓的动力理论的条件：_

（ⅰ）&中的任一简单谓词出现于T的一些规律语句中；

（ⅱ）&的任何谓词的外延（在任何时候）都是Dom的子集，或Dom的元素的有序n元组的集合；

（ⅲ）在&的规律语句推导中，T是封闭的；

（ⅳ）D的任一规律语句在T中是可解释的；

（ⅴ）F中没有规律语句在T中是可解释的；

（ⅵ）与F的元素n-eq的&中的任何规律语句也是F的元素；

（ⅶ）F的任一规律语句L₁有&的一个简单谓词出现，它也在F的其它规律语句L₂中出现，使得L₁与L₂不是n-eq的；

（ⅷ）&的基本谓词不出现于仅作为间接相关的F的规律语句中；

（ⅸ）&的谓词间的一切真等式都在I即真相等集合中；

（ⅹ）假如，α是&的一个n元简单属性谓词，使得满足α的任何有序n元组的分量k-th总是导出类，那么α是导出谓词（因此，导出属性也由基本谓词所限定的某些复合属性谓词来标记）。

当然，考西认为自己只是提出了科学统一的必要条件，而不是充分条件。他甚至怀疑一般的逻辑的和语义学的条件的任何集合能满足统一，因此关于统一科学还有大量的问题有待于进一步探索。