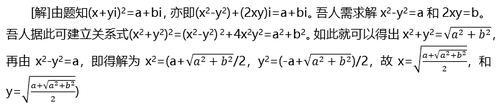解析:
1. 八卦之积方阵为一对称方阵,如表Ⅳ所示。
2. 八卦乘法符合交换律:z · w=w · z。
3. 主对角线上之元素示出各卦自乘这积为z · z=z2=(a+bi)2=(a2-b2)+2abi,形成一组以虚轴为镜面所反射的对称矢量(x,y)和(-x,y)。
4. 从对角线上之元素示出天与地、山与泽、水与火、风与雷四对互为二重性之卦之积符合(a+bi)(b+ai)=0+(a2 +b2 )i,即积为(0,25),(0,29),(0,37)与(0,49),均位于虚轴上面。
5. 在八卦乘法中,地卦等于实数因子7,任何卦与地卦相乘之积即等于该卦之7倍。
6. 在八卦乘法中,天卦等于虚数因子7i,任何卦(a+bi)与天卦相乘之积都等于(-7b+7ai)=7(-b+ai)。
7. 在八卦积方阵中共含64卦,除方阵四边及两对角上之卦(共40)合乎以上关系外,其他24卦均符合以虚轴为镜面的反射对称关系(a,b)与(-a,b)。
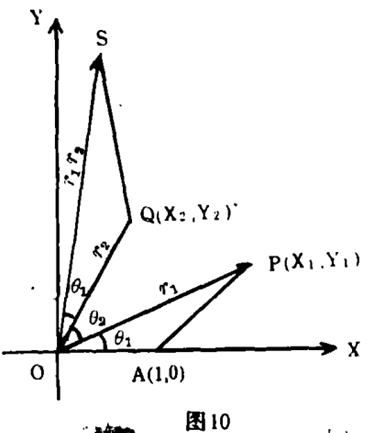
8. 八卦乘法之几何表示可由八卦矢量之极坐标(r,θ)求得,如图10所示。
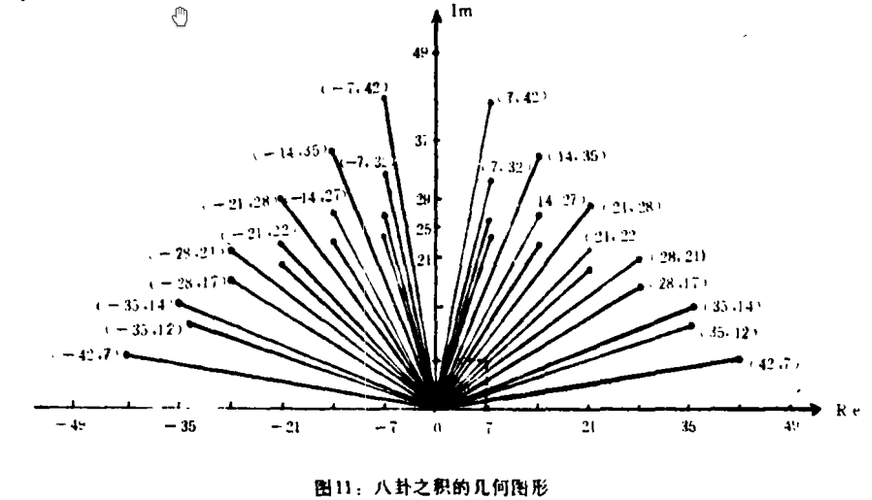
设x1=(x1+iy1)=r1(cosθ1+-isinθ1),z2=(x2+iy2)=r2(cosθ2+isinθ2),则z1z2=r1r2 (cosθ1+isinθ1)(cosθ2+isinθ2)= r1r2 {cos(θ1+θ2)十isin(θ1+θ2)},在复数平面中,根据几何关系,三角形OAP与三角形OQS相似,故z1与z2相乘之积z1z2为点s,并得出| z1z2|=os= r1r2=|z1z2|,和argz1z2 = θ1+θ2 = argz1+ argz2,变即积矢量之长度为两矢量长度之积,积矢量k之幅角为两矢量幅角之和。图11示出八卦之积的几何图形。
解析:
1. 八卦之商方解为一以实轴为镜面反射所形成的(a,b)与(a,-b)对称方阵,如表V所示。
2. 八卦除法符合Z/Z=Z · Z-1=1与W/E=W · Z-1。
3. 主对角上元素示出同卦相除之商为(1,0)。
4. 径对角上之元素示出互为二重性两卦相除之商形成以实轴为镜面的反射对称关系。
5. 在八卦除法中,地卦等于实数因子7,任何卦以地卦相除,其商为该卦之1/7,即Z/地=Z/7。
6. 在八卦除法中,天卦等于虚数因子7i,任何卦以天卦相除,其商为该卦之转变卦的1/7, 即Z/7i=(a+bi) /7i= (1/7) (b-ai)。
7. 在八卦除法中,地卦被他卦相除之商为:地/Z=7/(a+bi)=7(a-bi)/(a2+b2)。
8. 在八卦除法中,天卦被他卦相除之商为天/Z=7i/(a+bi) =7(b-ai)/ (a2+b2)。
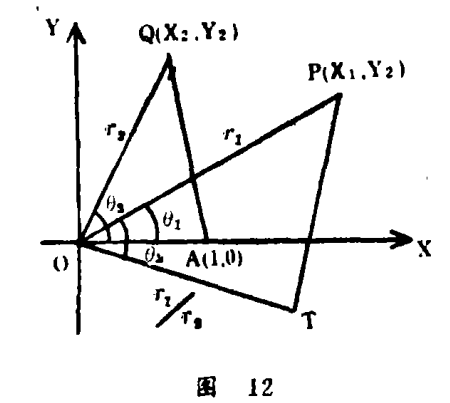
9. 八卦除法之几何表示方法可由八卦矢量之极坐标(r,θ)求得,如图12所示,设Z1=(x1+iy1)=r1 (cosθ1十isinθ1),Z2=(x2+iy2)=r2(cosθ2+isinθ2),则Z1/Z2=r1/r2{cos(θ1-θ2)+isin(θ1+θ2)},在复数平面内,根据几何关系,三角形OQA与三角形OPT相似,故Z1与Z2相除之商Z1/Z2为点T,并得出| Z1/Z2|=OT=|Z1|/|Z2|和arg(Z1/Z2)= θ1-θ2=argZ1-argZ2,亦即商矢量之长度为两矢量长度之商,商矢量之幅角为两矢量幅角之差。
10. 八卦之基本复变函数(Elementary Complex Functions of the Trigrams)
(A)易数之复变函数转换:在数学发展史中,复数集(C)是由实数集(R)的扩展而成,而复数面(Z)亦就是实数面(R2)的延伸,故而实函数的形成与转变原理亦可以延伸用于复函数,同理,易数既是复数,数学中的复变函数的转换原则也可应用于易数。
在复数面中,每一易卦系统构成一个易数集并位于一定域(Domain)内。易数集中每个构成元(Element)都是一个复数C=a+bi,它形成域内的一个点,或一个矢量,并可张成一个度量空间(Metric Space)。当将C作为变数时,其复函数式为Z=x+iy,它的两个构成基底为实数X和Y,当一复数域Z按照函数关系F转换(或映射)成为另一复数域W,这个转换函数关系式表作F:Z→W,其意义就是Z域中的易数Z转换成W域中的对应易数W,它的复数函数式为:
w=u+iv=f(z)=f(x+iy)=f1(x,y)+if2(x,y) (12)
式中函数f1(x,y)为复变函数f(z)的实数部分,f2(x,y)为其虚数部分。
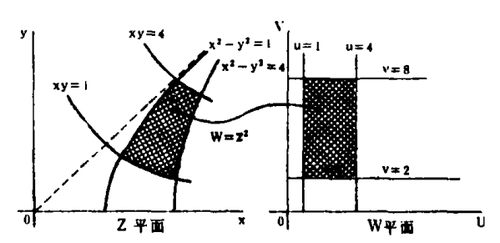
复变函数的转换示例如图13所示,图中表示w=z2=f(z)的Z→W转换关系,∵w=z2=(x+iy)2==x2-y2+2ixy;∴u=x2-y2,v=2xy。吾人选用u=1和v=2则x2-y2=1和xy=1,此二式在x-y平面中为双曲线。同理,u=4和u=8在Z平面中亦为双曲线,如是则Z平面中之阴影区域转换为W平面中之阴影区域。(如图13)
需要指出,在复变函数f(z)的作用下,如果一个点z(x、y)只能生出一个对应的w(u、u)时,吾人称f(z)为单值函数,如果可生出多于一个解的w值时,则f(x)为多值(multiple-valued)函数,但值得注意的是:f(x)=z2虽为一单值函数,却不是一一对应的,(因为f(-1)=f(1))。
易卦的复变函数转换,其领域浩瀚广大。本文限于篇幅,仅列出易数的若干基本复变函数,并以八卦为例表明,如下文所示。
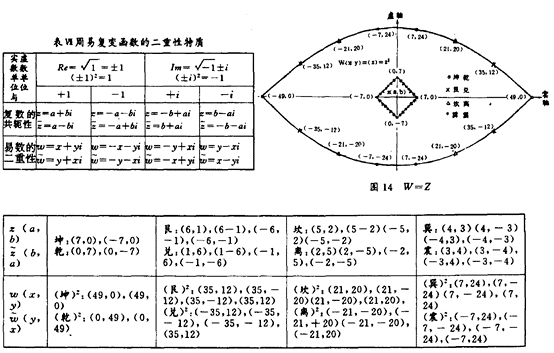
(B)周易复变函数的二重性特质:作者根据现代复数代数学建立了周易宇宙代数学,二者间存在着相互对应(Correspondence)与恒等[Identity]关系,亦即易数就是复数,复数的构成特质有二:(1)它是一个平面数,具有实数与虚数两部分,(2)建立复数的单位有四,即:
现以八卦为例,说明复数面中两个互为可逆的Z→W与W→Z转换。
(1)设z=a+bi,求解w=x+yi=f(z)=z2=(a+bi)2=(a2-b2)+(zab)i
[解]由对应系数知:r=a2-b2,y=2ab。又f(z)=z2虽为一单位函数,但却非一一对应关系,因f(-1)=f(1)。由易数的二重性关系(表Ⅵ),吾人可由八卦的序列Z(a、b),求出对应的w(x,y)=z2,列如下表:
根据表中的数据,八卦平方函数的转换关系W=Z2如图14所示:
(2)设Z=a+bi位于复数面内,求解面中必有另一复数W=x+yi,二者符合复变函数关系W2=Z。(当然,-W自亦符合此转换关系)
读者根据上解,即可代入八卦的序列Z(a,b),求出对应的函数关系式W2=(x+yi) 2=Z,并进而谱出W2=Z的转换图。
(C)八卦的代数多项式或函数:代数的基本定理必须建筑在复数域上,一个复变函数多项式可表为p(z)=anzn+an-1zn-1+…+a1z+a0,式中系数an可为实数或复数,a≠0,n≥1,函数p(z)=0至少含有一个实数或复数,an≠0,n≥1. 函数P(z)=0至少含有一个实数或复数根,最多可有n个根,如果P(z)=0含有一个实数根z=a+bi,则其共轭复数z-=a-bi亦必为一根,又根据因式分解原理,如果P(Z)=0含有r1,r2,…rn为根时,则p(z)=(z-r1)(z- r2)…(z-rn)。例如以易卦系统中的太极来说,它含有四个基数1. -1,i和-i,则太极的代数多项式必为P(z)=(z-1)(z+1)(z-i)(z+i)=(z2-1)(z-i2)=z4-1,而太极就有成为代数基本定理的基础范例。
关于代数多项式的理论及其根与系数间的关系,读者可参读专书,不在本文范围之内,作者现要建立的是八卦多项式的生成原则。易卦系统的衍生是准照多项式的顺序,多项式是以线性代数式a1z+a0开始,此即相当于太极生两仪,故两仪就是构成易数的两个基元,但易数必须由实、虚两部分才能构成一个完全的复数z=a+bi,在易卦的衍生层次上,只有象中的少阳,z=2+1i和少阴,z=1+2i才是构成一切易卦的两个基本因子,作者将此归纳为一定理曰焦氏易卦多项式定理:“每一易卦都可展成为少阴z=1+2i或少阳z=2+1i的三次代数多项式z3+az2+bz+c;式中系数a,b,c为实数”。
现以八卦中的震卦与六爻卦系中的鼎卦为例,证明上述定理。
[例1] 证明震卦3+4i可表为少阳2+1i的三次多项式
解;令3+4i=(2+1i)3+a(2+1i) 2+b(2+1i)+c
展开上式:3+4i=(3a+2b+c+2)+i(4a+b+11)对应系数得联立式:3a+2a+c-1=0与4a+b+7=0
解为a=-3+c/5,b=5-4 c/5,故依c值而有许多不同解的组合
当吾人选定最低的适宜值c=5,和c=-5时,则得出下二组解:
(1) C=5,a=-2,b=1。(2)c=-5,a=-4,b=9
故
(1) 3+4i=(2+1i)3-2(2+1i)2+(2+1i)+5
(2) 3+4i=(2+1i)3-4(2+1i)2+9(2+1i)-5
同样亦可求解3+4i=(1+2i)3+a(1+2i)2+b(1+2i)十c
两组解可为
(1) c=1,a=-2,b=7;
(2) c=-4,a =-3,b=9
故
(1) 3+4i=(1+2i)3-2(1+2i)2+7(1+2i)+1
(2) 3+4i=(1+2i)3-3(1+2i)2+9(1+2i)-4
[例2] 证明六卦系中的鼎卦34+29i可表为少阳(2+1i)的三次多项式
解:令34+29i=(2+1i)3+a(2+1i)2+b(2+1i)十c
展开上式:34+29=(3a十2a+c+2)+i(4a+b十11)
对应系数得联立式3a+2a+c-32=0与4a+b-18=0
故得出两组解为(1)a=1,b=14,c=1与(2)a=-1,b=22,c=-9
故
(1) 34+29i=(2+i)3+(2+i)2+14(2+i)+1
(2) 34+29i=(2+i)3-(2+i)2+22(2+i)-9
同样亦可求出34+29i=(1+2i)3+a(1+2i)2+b(1+2i)十c
(D)八卦的指数函数(Exponential Function):在代数学中,复函数是实函数的延伸,二者间的定义、性质与操作必须对应符合。例如根据级数式ex =1+x/1!+x2/2!+x3/3!+……,当将实数x延伸为虚数yi时,则得出定义eiy=1+ iy/1! +( iy)2/2!+……,将此式再行组合为eiy=(1- y2/2!+ y4/4! +……)+i(y- y3/3!+ y5/5! +……),就知它和权函数(Power Function),cosy+isiny完全相合,如此就建立了虚数指数的基本定义:eiy=cosy+isiny. 再根据指数的性质,吾人就得出复数的指数函数定义谓:令z=x+iy,则ex=ex+iy=ex · eiy =ex(cosy+isiny)。当将复数z还原为实数x时,则y=0,结果就是实数恒等式ex =ex 。
有关ex的各种性质和运算,读者可参阅专书,作者现只指出ex为一周期函数,其周期为2x。
本文篇幅所限,不能对八卦的指数函数多作论述,下面仅只列出八卦指数函数的和(即积)方阵(表Ⅶ)且采用了减缩的指数函数定义式:ex=ex+iy=ex(cosy+isiny)= ex(cisy)(例如离卦的指数函数为:e2+5y=e2[cos(5)+isin(5)]=e2cis5)
表Ⅶ八卦指数函数的和(积)方阵
ex+w=exew=e(x+iy)+(v+iu)
={ex(cosy+isiny)}{eu(cosv+isinv)}
=ex+u{cos(y+v)+isin(y+v)}
=ex+u(cis(y+v)) (13)
(E) 八卦的三角函数(Trigonmelric Functions);根据指数函数公式
eiy=casy+isiny e-iy ==cosy-siny (14)
可以得出siny= (eiy-e-iy) / 2i cosy= (eiy+e-iy) / 2 (15)
将上面实数三角函数延伸到复数三角函数,就得下面定义
sinx= (eix-e-ix) / 2i cosz= (eix+e-ix) / 2 (16)
兹将复数三角函数的若干重要性质,列出如下:
(1) sinz是一奇函数,因为sin(-z)=-sinz;cosz是一偶函数,因为cos(-z)=cosz。
(2) 当sinz=0,则e2iz=1,即2iz=2kxi,故z=kx,当cosz=0,则e2iz=-1,即z=π/2+kπ,式中k=±0,±1,±2,……
(3) 根据sinz和cosz,可以得出(a) sin2z+cos2z=1,(b) tanz=sinz/cosz,z≠kπ,(c) cotz= cosz/sinz,z≠kx,(d) secz=1/cosz,z≠π/2+kx,(e)cscz=1/sinz,z≠kx。
(4) sin(z+w)=sinz · cosw+cosz · sinw和cos(z+w)=cosz · cosw-sinz · sinw
本文篇幅所限,不能对八卦的三角函数多加论述,下面示出计算正弦函数与余弦函数的两个例题,并将八卦的正弦与余弦之值列于表Ⅳ。
例题:计算sin(1+i)与cos(2+3i)
解:sin(1+i)=(2i)-1{ei(1+i)-e-i(1+i)}= (2i)-1{e-1+i-e1-i} =(2i)-1 {e-1(cos(1)+isin(1))-e(cos(-1)-isin(-1))}=2-1sin(1)(e-1+e)+i2-1cos(1)(e-e-1)
cos(2+3i)=2-1{ei(2+3i)-e-i(2+3i)}=2-1{e-3+2i-e3-2i}=2-1{e-3(cos(2)+isin(2))+e3(cos(-2)+isin(-2))}=2-1cos(2)(e3+e-3)+i2-1sin(2)( e-3-e3)
(F) 八卦的对数函数(Logarichmic Function);在实数域内,对数函数与指数函数形成两个互为可逆的函数转变关系,当y=ex时,它的解就是logy=x。因为指数函数为一多值函数,且永不为零值。故对数函数亦必具有此二性质,当将此种函数关系延伸到复数域内,则在复数平面中,对于任一不为零值的z=x+iy,亦必存在另一复数w=u+iv,二者符合函数关系w=logz,其逆函数就是z=ew,吾人称w为z的对数。
本文篇幅所限,不能对八卦的对数函数多加论述。但作者必须指出一点:在一般情况下,对数关系式log(z1 · z2)=logz1+logz2不能成立,现用下例题证明此点,并示出计算对数值的方法。
例题:计算z1=i,z2=-1+i,和z3=-1-i三者的对数值,并用此三对数值证明log(z1 · z2)≠logz1+logz2
解:log(i)=loglil+iargi=log1+iπ/2=iπ/2
log(-1+i)=logl-1+il+iarg(-1+i)=log![]() +i(3/4)π=2-1log2+i(3/4)π
+i(3/4)π=2-1log2+i(3/4)π
log(-1-i)=logl-1-il+iarg(-1-i)=log![]() -i(3/4)π=2-1log2-(3/4)π
-i(3/4)π=2-1log2-(3/4)π
但吾人可示出z1 · z2=i(-1+i)=-1-i
故可证明log(z1 · z2)=log(-1-i)= 2-1log2-i(3/4)π≠log(i)+log(-1+i)=i(π/2)+2-1ln2+ i(3/4)π= logz1+logz2
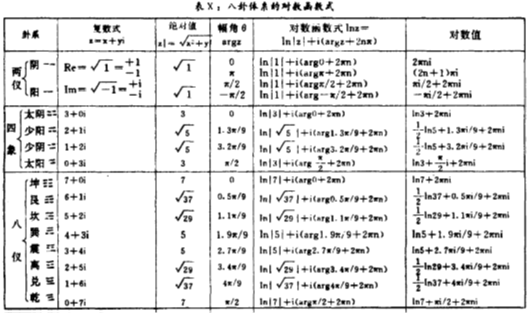
根据八卦体系的复数基本关系式(表Ⅱ),作者将八卦体系的对数值的计算列成表X。
结 语
作者基于下列三个目的:
(一). 为对中国古代传统文化的继承、重整与发扬工作开路。
(二). 为将东方古代哲学文明与西方现代科学文明的整合奠基。
(三). 为促进中国文化成为廿一世纪的世界文化的主流尽力。
进行了建立《焦氏周易宇宙代数学》的研究工作,作出这篇开创,启蒙性的研究论文,敬请中国和世界的专家学者指教与批评。
最后,作者赖以五言诗一首,结束本文。
要作智慧人,先识河洛易;
阴阳实虚变,生命展真谛。
参考文献
[1] 焦蔚芳:《洛书的数学研究——焦氏“洛书矩阵”学说》,世界科学,1987年第5期,P23一26
[2] 焦蔚芳:《洛书的数学研究之二——焦氏“洛书数字几何学”导论》,世界科学,1991年第3期,P6一14
[3] 焦蔚芳:《洛书的数学研究之三——焦氏“河洛数论探源”》,世界科学,1992年第8期,P3一8;第9期,P9一12
[4] Carl G. Jung,“Man and his symbols”,Doubleday & Compang,9nc,Garden City,New York,1964
[5] Abraham Pais,“Bohr‘s Century,Neils Bohr‘s Times,in Physics,Philosophy,And Polity”,Oxford University Press,1991
[6] Kerson & Rosemry Huang,“I Ching”,Workman Publishing,New York,1987
[7] 王赣,牛力达,刘兆玖,“古易新编”上,黄河出版社,1988
[8] D. L. Livesey,Am. J. Phys. 30,629(1962)
[9] Carl B. Boyer,“A History of Mathemathics”,2nd Ed. John Wiley & Son,Inc,New York,1991
[10] Colin A. Ronan & Joseph Needham,“The Shorter Science & Civilisation In China:l”,Cambridge University Press,1978
[11] 董光壁,“易图的数学结构”,上海人民出版社