比类，是我国传统的数学方法之一。最初，把按一定规律堆积起来的物体与相似的立体几何模型相比较，从已知的体积公式推出各种垛积公式（即高阶等差级数公式），叫做比类。以后，用按一定规律的计算替代实物，加以观察和比较，得出更吸引人们注意的成果，如元代朱世杰《四元玉鉴》（1303）中所提出的一些著名的垛积招差公式，便由此取得。一般说来，这种方法比较简单，用现代的水平来衡量，其成就，只属于数学的初等阶段。但经过大胆想象，从常人未曾想过的新的角度上着手，进行辛勤的计算（这也是一种实验），仔细地观察和归纳，则即使所应用的方法较为古老和简单，也能取得不寻常的成果。我国清代著名数学家李善兰（1811-1882）所创造的“垛积差分”方法和由他创始的李善兰多项式，就是用“比类”而得出的既具有中国的传统特色，还能与近代数学挂起钩来的，独树一帜的数学成就。

李善兰的上述成就，集中表现在他的名著《垛积比类》四卷中。这部书从三十年代以来即受到中外数学家和数学史家的注意。1982年在杭州举行的李善兰逝世一百周年纪念学术讨论会和在比利时鲁文大学举行的中国科学史第一次国际会议，都曾讨论了《垛积比类》，并因其可与现代的有限差分、组合分析发生联系而取得较高的评价。同时期的杂志和学报亦曾发表有关的研究论文多篇。因为此书取法别出蹊径，不易为人所知，对李善兰究竟采用什么方法得出书中许多有价值的等式，迄无定论。正如李俨先生所说：“值得提出的，李善兰（在《垛积比类》中）还只是列出这些等式，并没有提出完整的证明。由于文笔过于简略，不易揣详，关于李善兰的整个思路，还待作进一步的研究。”[2] 据笔者所知，李善兰在《採积比类》中继承并发扬了元代朱世杰的垛积招差、利用杨辉三角的特殊性质，结合我国古代的开方法，创造了独树一帜的差分方法（因与现行各种差分方法取径不同，暂从原来出处取名为“垛积差分”）使用比类方法从而得出书中的等式，为解决这件中国数学史上的疑点，便于继承、借鉴和推广，略述“垛积差分”的来由以及李善兰在《垛积比类》中的等式是怎样取得的。

一、垛积差分概述

1. 取得垛积差分系数

以上就是取得垛积差分系数的方法，其他幂函数可以类推。由此我们可以看出，现在通行的牛顿、高斯、贝塞尔、司脱林等以西方人命名的差分公式，他们所取的差分系数的位置所在，都与函数序列相交且在它的右侧，而垛积差分系数，则是与函数序列平行的，故是不同的。

2. 用垛积差分系数与二项式系数的乘积之和来表出函数序列（u_j）与各次和（∑^h）

垛积差分系数是由函数序列向上累减而取得的。反之，用垛积差分系数向下累加，就可得出函数序列，再累加，便得各次和∑^h

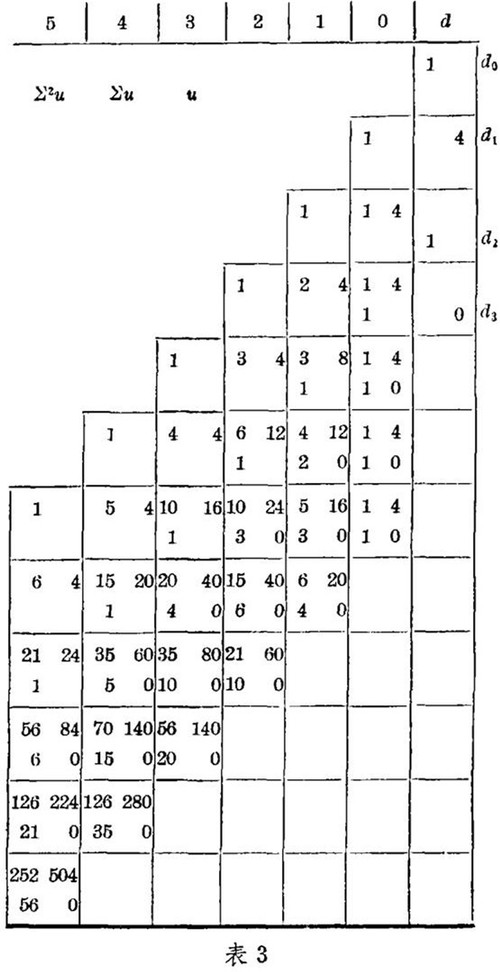
例如把表2中的垛积差分系数1、4、10依次放在大方格内，使左、右、上、下各居一隅，并按隅向下累加，便如表3。

表3最右一列，从上到下，在左上角的是第一层1个“三角”（d₀），在右上角的是第二层4个“三角”（d₁），在左下角的是第三层1个“三角”（d₂），在右下角的是第四层0个“三角”（d₃）。《垛积比类》用古代开方法名词，称d₀为方，d_n为隅，若d_n=0，则称d_n-1为隅。d₁以下分别称为甲、乙、丙、……诸廉，至隅前而止。

根据上面的论述，可以看到李善兰怎样取得《垛积比类》中各卷的等式的。为解答中国数学史上这个“难以揣详”的疑点，把《垛积比类》四卷中各卷内容，试析如后。

二、《垛积比类》各卷的内容与取得公式的方法

卷一   三角垛

（1）在这一卷的上半部分中，李善兰先揭示了如例1的杨辉三角（二项式系数表），并提出二个基本公式：

该书意在阐明“垛积差分”，但以连乘积列术，是使人“难以揣详”的原因之一。

卷二   乘方垛

观察从序列1n、2n、3n、…所取得的垛积差分系数

当n=1时，有d₀=1，d₁=0

当n=2时，有d₀=1，d₁=1，d₂=0

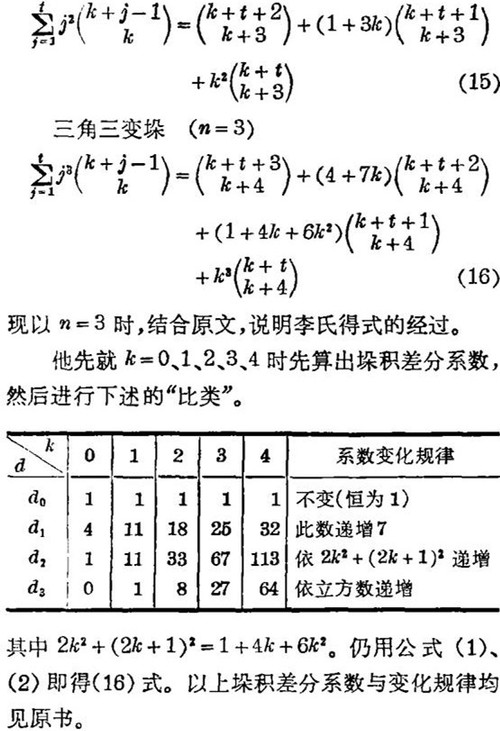
当n=3时，有d₀=1，d₁=4，d₂=1，d₃=0

把这些n次函数的d_i换写成A_nⁱ⁺¹，便有如表4的“乘方垛各廉表”。也就是组合分析上的计数函数“欧拉数”（Eulerian numbers与通称Euler's numbers者不同）

这个表实际就是前面的表2，但是没有显示垛积差分系数，仅在附注中点出。这两个表相互对照，可知李善兰取法的来由。

卷三   三角自乘垛

在这一卷中，李善兰作出了著名的李善兰恒等式，曾引起了中外数学家的广泛注意，并提出多种证明。［5] 中对之有详细的介绍。如果利用本文的公式（6），及二项式系数的垛积差分系数d₀=1，d₁以上为零的性质，可立即得证更较简捷。李善兰的推导过程约略如下：

1939年，章用在［3] 中创立了递推公式，推广到任意的n变，并列出李氏三角形。罗见今同志说，这是“第二种李氏数（欧拉数）的推广”，为“外论所未见”，“迄未所闻”的。［6] 法国数学史家J. C玛尔茨洛夫1982年8月在“国际中国科学史讨论会”上发表的论文《李善兰的有限和公式》中说：“第四章（即第四卷‘三角变垛’）的公式，只要进行代数计算就够了”，所举的仅是时的别解。可见迄今为止国内外对此了解是不够的。现在看来这是一个丰富多彩的特殊多项式，与组合分析、有限差分有许多联系，不但与第一类司脱林数，欧拉数有联系（这是中外论述已提过的），还与第二类司脱林数，与幂函数的各种表达式有联系，详细的论证与推广有拙稿《广揉积比类》，其推广、组成与应用在［8] 、［9] 中有简略介绍。

“垛积差分”还有其他功用。由这种差分的特殊对称性，可论证组合分析中两种司脱林数的合一，及推出沟通这两类“数”的数φ_rⁱ［8］等等。是有继承、推广和研究的价值的。

最近，中共中央宣传部和中共中央书记处研究室发出《关于加强爱国主义宣传教育》的重要文件，把“宣传历代杰出的科学家及其贡献”作为主要内容，之一，对这项杰出的我国数学成就，作进一步探讨，与现代的组合分析、有限差计算结合起来研究，迈出一条有中国特色的路子，该是很有意义的。

参考文献

[1] 清·李善兰：《垛积比类》（1867）

[2] 李俨、杜石然：《中国古代数学简史》（1964）

[3] 章用“垛积比类疏证”《科学》1939（11）23

[4] Riordan，J An Introduction to Combinatorial Analysis（1958）

[5] 罗见今“李善兰恒等式的导出”，《内蒙古师院学报》，1982第二期

[6] 罗见今“李善兰对Stirting数和Euler数的研究”《数学研究与评论》，1982（2）4

[7] 法·J.C马尔茨洛夫“李善兰的有限和公式（罗见今译）”《科学史译丛》，1983第一期

[8] 傅庭芳“简介李善兰和‘垛积差分’”，《世界科学》，1982第七期。《对李善兰〈垛积比类〉的研究——兼论垛积差分的特色》，李善兰逝世一百周年学术讨论会，（1982）。——本人著