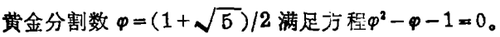“数学是科学的皇后,算术又是数学的皇后”,高斯这样说。他这里所说的算术是指数论,不是2+2=4,关于皇后一尘不染的倾向他还未完全忘怀。数论的外现的主题——普通整数的模式和复杂性——不会使人联想到对科学的直接应用。鲍尔(W. W. Rouse Ball)于1986年写道:“这门学科本来是特别有趣和优美的学科之一,但它的结论很少有实际重要性”。按照数学分属于“纯粹的”和“应用的”这个通常分法,数论大约是你所能得到的最纯粹的:它与传统的应用学科例如动力学完全相反,如此而已。
至少有10年之久,显示数论有用的证据越来越多。施勒德(Manfred Schroeder)的书“数论在科学和技术中的应用”(Number Theory in Science and Technology)作出了一个令人信服的范例,现在,伦敦玛丽女王学院的帕西瓦尔(Ian percival)和维瓦尔迪(Franco Vivaldi)已经发现了数论深奥抽象的概念对于数学物理最兴旺最有魅力和最时新的研究领域之一——紊乱动力学的广泛应用,(见波尔和柯维塔诺维克的评述文章“紊乱是物理学的喜讯”)。
他们的方法取自代数数论——指代数数的理论而不是数的代数理论,让我先来叙述这个概念。一个复数是代数数是当它能满足一个系数为有理数的多项式方程;说它是代数整数是当这些系数都是整数。例如,
与数φ相关联的是它的数域,这个数域由所有形如p+qφ的数组成,这里P和q是有理数;以及它的整环,其中P和q必须是整数,代数数论研究这些代数整环的算术。其中心概念是“理想”(ideal)概念。引进这个抽象的精巧的概念,是为了约束代数数被分解为素数时头绪纷杂一发不可收的倾向。它起源于库默尔(Ernst Eduard Kummer)的研究,他原先的部分目的是解决费尔马大定理:当n≥3时方程xn+yn=zn无整数解。此定理至今仍未解决,虽然最近的研究表明,要证明它已为期不远。
关于术语已说得够多的了;现在要述及主题内容,紊乱动力学是一门动力学,是属于数学,物理学和生命科学的边缘使人振奋的新领域。它开始于晚近才观测到的事实:所谓完全决定性系统的行为可能是随机的。紊乱向经典数学模式的整个哲学提出了挑战。
紊乱在其中起决定性作用的首要领域是哈密顿系统,即无摩擦的动力学研究,近代对于哈密顿系统的探讨方法是几何的。此系统的位置和动量变量限定了一个多维“相空间”。例如自行车的运动可能至少有5个自由度。前轮可以旋转并指向任何方向,同时后轮和齿轮系统,以及两个踏板能独立地旋转。自行车的位置对应于5维环面上的一点,在5维欧几里德空间中又有各种角动量,自行车的相空间结合这两者,因此是10维的。自行车的运动可由一个在10维相空间中的动点的运动表示,它是遵从牛顿动力学的。在考虑自行车所有可能运动时,我们从相空间中每个起点确定一条这类道路;这些道路相似于在液体中悬浮的粒子描出的那些路线。因此动力学被看作为通过多维相空间的理想液体流。
经典应用数学描述充分规则的流运动。庞加莱是第一个发现,你的典型的普通的哈密顿系统确有可能是以很不规则的方式行事的,他视为畏途,没有进一步进行分析。苏联数学家阿诺德(Vladimir Arnold)曾很有理由地说,对一个典型的哈密顿系统的分析是“近代科学无能为力的”。其理由是在这类系统的相空间中,一方面有规则行为的“椭圆形孤岛”,一方面又有随机行为的“杂乱聚集物”,这两者像肉丸和通心面不可名状地缠结在一起——动力学的大红肠。
帕西瓦尔和维瓦尔迪从以下事实着手:“有两种特别类型的极限系统从这种有毛病的结构脱颖而出,即可积分的系统,是纯粹规则的;以及安诺索夫(Anosov)系统,是纯粹紊乱的”。他们把注意力放在后者,集中于,离散动力学中这一相对地被忽视但却重要的情形。
离散动力学从某个初始状态开始并随着固定时刻1,2,3……按某个固定的规则演化。最简单的行为是保持原初状态不变。在这情形,它称为这个动力学的不动点和稳定态。其次简单的行为是周期循环状态,无休止地重复某些有限系列的构形。除此而外,还有伪周期行为,其中几个独立周期实际上是叠合的:此系级几乎重复它的演化。
紊乱是戏剧性地不同:它实际上是不可预见并完全随机地出现的。但是,即使在紊乱系统中,也有某些初始状态是以精确的周期演化的。它们之所以未被观察到是因为它们是不稳定的,并被某些不规则地演化的一些状态掩盖了;但是它们仍然形成一个规则行为的基本骨架,而一些紊乱行为好比肌肉附着其上。因此这使某些紊乱存在的真实性有了弱点,受到持决定论观点的数学家们的攻击。
帕西瓦尔和维瓦尔迪的目标是要弄清楚纯粹紊乱系统周期状态的算术性质。一个给定周期的紊乱状态存在吗?有多少?在何种情况下?他们取一个2维环面作为相空间——用经典名词,一为位置坐标一为动量坐标——其动力学是用环面到自身的映射反复迭代而成的。
我来举一个例子。环面上一点由它的坐标(x,y)所决定,这里x和y取值在o和1之间。映射规则是:使(x,y)对应于(x+y,x+2y)如果这些数大于1,就只取它们的分数部分。几何上说,这个环面将伸长,旋转并放置在自身之上(这个映射被戏称为阿诺德猫,是由于阿诺德在环面上画出一幅漫画猫作几何演示之用,以此得名)。
这个运算的特征值(它量度沿着主方向拉长或收缩的程率),是代数数。帕西瓦尔和维瓦尔迪证明了,关于这个映射的动力学的许多特征可以复述为关于特征值的算术的问题。对于这个阿诺德猫的映射,黄金分割数φ是一个特征值:阿诺德猫的动力学是由黄金分割数的算术所决定。
此方法对任何广义的猫映射也成立,其系数为整数,由2×2双曲型矩阵所限定。广义猫映射的性质和周期点的个数能推导出来,正是应用了大量代数数论的经典方法,比起笨拙的计算更为有效。这些内容包括理想论、理想类、二次互反律、范数、基数以及素数的分类。帕西瓦尔和维瓦尔迪概括地说:“我们这里所用的大部分概念是在19世纪末之前发生的,至今它们对于现代非线性动力学的发展很少有触动。这些方法不仅提供了有效的计算工具,也使人看到不规则轨道的内在结构,而此不规则性与代数整数理论共有同样的丰富多彩和不可预见性。”
数学充满着奇异的东西,从这个新发现的关于费尔马定理和动力学之间的联系说得很清楚了。特别奇怪的是这两者之间的联系是既自然又优美。新成果的不断流出是如此令人感兴趣,以致使人易于忽视在其后面的景象的深度。这是一个奇异的例子,它说明了把熟知的但显然不相关的技巧结合在一起能得到怎样的结果。某些成果激发了人们在数学家的故纸堆中最被忽视之处的钻研,而另一些成果则充实了物理学家的工具箱。谁知道还有什么东西,被弃置在黑暗中,正等待它的光荣的时刻到来?
[Nature,1987年10月]