历代学者一直认为摆是简单而有规律运动的典范。事实上,摆仍然有不少使我们惊奇之处。
在近来发现的关于摆的紊乱和不可预见行为中有两件事可能使你惊讶不已。人们熟识摆,并研究摆已有几个世纪之久,谅必已经一清二楚。其次,摆是规律性的集中体现;似乎摆的行为不可能是紊乱或不可预见的。但它们确实被否定了。
使我们吃惊的不仅是摆的行为。不同系统例如简单电子电路,电机,激光,化学反应和心肌细胞的行为也同样是紊乱的,并且其意义所及远远超出这些例子——例如天气预报,生物种群,丁口数,生理和精神病学,经济预报,也许还有社会进化等事项。
我们所考虑的典型的摆可以简单地由悬挂在绳子一端的一个球组成。这个被悬挂着的球可以在任何方向上摆动。这类摆称为“球面摆”或“圆锥摆”。我们能迫使悬挂点在水平直线上振动,例如用一个曲轴加以驱动。这个驱动振动的振幅与此摆的长度相比很小,但其频率接近于此摆自由摆动的频率。
你猜想这个摆会怎样摆动呢?你大概会推测——完全正确地——摆球将在平行于驱动振动方向摆动,并且由于驱动振动频率接近于摆的固有频率(当它自由摆动时的频率),此球将可能作大幅度摆动。很难预见的是——但是真的——这个球也可能产生一个垂直于驱动方向的运动,并且这两个方向的运动相结合的结果可能是非常复杂的。特别是,如果驱动频率在某个特定范围内,要预见摆将如何运动是不可能的;在设想是相同的条件下,一次接一次的实验总产生不同的运动模式。
但是控制摆运动的自然定律仍然是没有疑问的。它们正是牛顿经典力学定律,它们完全是决定性的定律。如果你精确地知道摆在某个时刻的运动状况,原则上你能完全决定它随后的运动。这样的决定论与实践中可预见性的缺少在原则上并不矛盾,这种认识对于我们过去十多年的思想有重要影响。
摆的行为是“决定性的紊乱”的一个例子。我一无所知摆的紊乱运动的实际应用——而且我真的不指望有一项实际应用。但是正如我前面提出的,决定性的紊乱的概念有很多高度重要应用。由于摆的简单性。
它提供了极好的一个有助于理解这个概念的来龙去脉的例子。
我们关于这类摆的行为的知识是从加利福尼亚大学的迈尔斯(John Miles)的数学研究开始的。我自己的贡献是制造出一种仪器用以演示出有序运动与紊乱运动之间的区别。
你所观察到的是摆球运动在水平方向上的投影。换句话说是你从上面俯视所看到的球的运动。所有有趣事件出现在驱动频率与摆自由运动的固有频率相差不超过百分之几的时候。在这个频率范围之外,摆在平行于驱动方向的摆动振幅相对较小。在这个有趣的频率范围内,对驱动频率作逐步的微小的改变,会产生各种细微的行为。然而这两种呈鲜明对照的行为类型各自出现在一个充分宽广的频率范围内,要发现它们是很容易的。
第一种类型。它不是紊乱运动的例子,典型地出现在驱动频率略高于摆的固有频率之时。在驱动开动之后的一刹那间,摆球作平行于驱动方向的摆动。因为这个频率与固有频率相合拍,这些摆动最终达到一个本征幅度。然后此运动开始产生一个垂直于驱动方向的分量。在一系列复杂的反复的波澜起伏之后,此运动最终归结为一个规则的模式。此球在一个近似圆形的轨道上运动——在每个驱动周期内绕“圆”一周。——当这个模式确立之后,它将随着驱动的保持而永远保持下去。
甚至这个非常规则的运动也不是完全可预见的。至少有一件事是我在开始演示之前所不能预见的:此球将以顺时针方向还是以反时针方向运行呢?如果我做这个实验许多次,则这两种情况随机地出现。然而一旦我观察到哪一种情况已经确定,则我能早早地完全地预见其运动。
可预见性的缺少(虽然在这种情况并不明显),表现在由于平行于驱动方向运动的不稳定性引起了垂直于驱动方向分量的产生。虽然控制这个运动的方程形式上有一个无垂直方向运动的解,但是这个解不会实现,因为与完全平行方向运动的任何微小岐离将导致更大的岐离。相似地我们不能使一支铅笔以笔尖着地竖直倒立。虽然此方程有一个以重心在支点的正上方,铅笔保持静止的一个解,但是偏离这个位置的最轻微的运动使各个力重新调整,致使铅笔倒下。在这种情况,也有不可预见性的事;如果你试图使铅笔保持完全平衡,但你不知道它将向左、向右还是向前、向后倒下。
我们能理解摆的上述运动,正如我以上根据它们长期运动的结局所述的。正是当你将驱动频率调整至典型地略小于固有频率时,才出现了真正意外的事。那时你可能从摆看到什么呢?
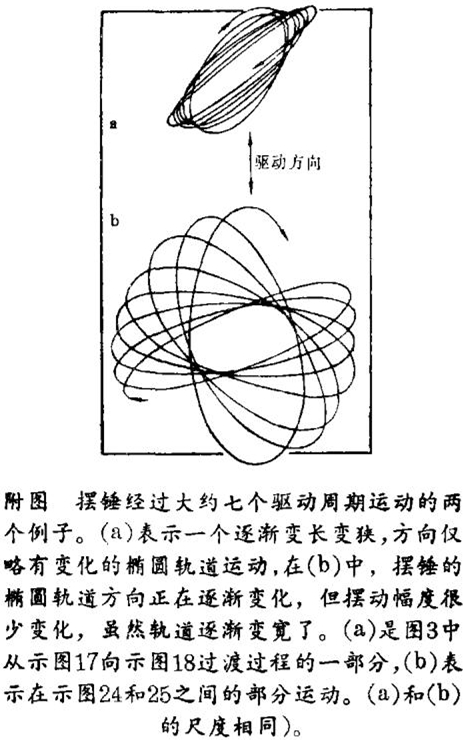
附图表示许多可能解答中的两个解答。每一个示图是此摆锤在几个周期内的一个轨道。相继的轨道相似但不相同,所以在几个周期以后实质性的变化出现了。每个轨道近似地是一个椭圆(它有时变得那么狭窄,实际上形成一条线),但是大小、方向及长与宽之间的比例都变了。特别要注意到在顺时针运动和反时针运动之间的频繁转换。对于这些变化并无可识别的模式。长期的观察结果——并结合迈尔斯(Miles)的理论研究——有力地说明并无可识别的模式。这些变化是紊乱地出现的。
当摆以这种方式运动时,摆球运动的观察结果对预见它随后的运动的参考作用非常有限。假定我们获得了摆球过去一段运动过程的非常细致的观测结果(例如在一个驱动周期内的),并将这些数据输入计算机,对这些数据我们已经运用摆的运动方程或对它的行为的许多以前的观察结果加以程序化了,然后我们着手去预见此摆随后的运动。我们的预见与运动的实际演化将会符合到怎样的程度呢?在一刹那间,在预见和观测之间将有令人满意的符合。然而、或迟或早这个预见必定要失败。我们输入计算机的观测数据越是精细,符合的时间会持续得越长,但最终这两者要分野。
“对于初始条件的敏感性”这个概念起理解为什么决定性并不一定意味着可预见性的关键。如果我们真正确切地知道摆在一个给定时刻是如何运动的,则我们就能确切地预见它将来的运动。但是我们从未能真正确切地知道任何事情——例如驱动力轻微的振动或房屋内最轻微的拖曳都使我们无法精确地知道这个摆的运动。紊乱行为系统不同于有序行为系统的特征是在紊乱系统中最微小的行为变化最终引起十分不同的细微的发展。
这类紊乱行为也能由各种数学方程(或—组方程)所给定,这种认识已经使我们过去十多年的思想根本改变了。这个受迫运动的球面摆仅仅是紊乱系统的一个例子——虽然,以我之见,它是说明这个基本概念的—个相当好的例子,许多其他系统的行为与此相似。科学家们已经研制出这类系统的其他简单示例——例如在究变磁场中的磁针,对车轴有作用力的电动机,在两个磁体之间弯曲的粒子束,带有线圈和二极管的简单电子电路。然而我们不应把决定性的紊乱主要看作为娱乐性的演示。决定性的紊乱对于我们理解自然界和对于我们试着预测实际重要系统的行为这两个方面具有深远的意义。
在我引进一两个这类例子之前,我将关于有可能显示出紊乱行为的系统的类型提出一个进一步的观点、就是说它的基本方程必须是“非线性的”。摆能说明这是什么意思。摆自由摆动的周期与它的摆动幅度的大小无关,否则人们也就不能利用摆去控制时钟的走时了。然而如果摆动幅度大到一定程度,这个规则不再成立;当作大幅度摆动时其周期是与幅度有关的。发生这个变化的理由是将摆锤拉向竖直位置的引力转矩当角度很小时是与角度成正比的,当角度较大时不成正比。偏离正比是非线性的特点之一。
当心紊乱
因此,紊乱行为仅能伴随非线性系统出现,这个事实解释了为什么一个受迫振动的球面摆仅当驱动频率接近于固有频率时发生紊乱的原因。仅在这时摆动才能渐渐达到充分大的幅度使非线性因素抬头。
我们生活在一个非线性世界里;否则它是多么单调乏味;可以毫不夸张的说几乎没有一个科学分枝将来不被我们对于非线性系统性质进一步的理解所触及。这些性质虽然各异,但它们以多种隐微的形式隐藏着紊乱行为的事实,最终为我们的思维所接受。
这个紊乱事实已被重视的一个所在之处是天气预报一不是在逐日预报的问题上而是天气预报的有效期是否有一个基本限度,是否值得花费大量投资用在收集数据的系统方面和试图延长预报期限的计算能力方面以获得有用的预报?但是至少大气环流的某些方面表现出对起始条件的敏感性。
关于紊乱行为的概念对于科学家研究动物种群丁口数的动态也是重要的、确实这个应用激发了某些基本理论研究——这是生物科学比物理科学对应用数学的发展起了更重要促进作用的相对很少的几个例子之一。例如,为什么某些种类甲虫的数量猛增猛减?蝗灾就是显然的一例。显然天气是一个重要因素,把我们带回上一节末那个问题。然而,很可能某些种群丁口数的增减方式本质上是紊乱的,甚至在假想的天气一成不变的地球上这些蝗灾仍有可能出现。
紊乱行为可能对于诸如化学工程和医学等学科有意义。在工业设备中所观测到的某些化学反应过程发生紊乱的含义是什么?有可能解释正常系统向紊乱状态转移的临界条件吗?我在这里仅能提出而不能讨论这个问题。
人们现时正在讨论紊乱行为与社会科学的关联。显然最有可能的应用是在经济预报方面,而且这类紊乱行为也可能与社会演化的各个方面有关。但是我们能利用一组方程的性质来讨论经济和社会系统吗?每当我们阐述某个真实系统的数学模式时,我们作出假定和近似。在物理科学中,对于高度有效的模式分析我们通常有信心认为这个模式与实际情况充分符合。在其他学科,我们可能缺乏这种信心。然而我们所归结的方程几乎必定是非线性的。如果我们不能归结出一个有用的数学模型,其内在过程也毫无疑问是非线性的;当简单非线性系统尚且产生复杂行为则复杂非线性系统也是如此。含意是清楚的,从紊乱找答案。
我本想说到这里为止,突然想到可能有些读者认为这是一个非常悲观的结论。可想它意味着,或迟或早某些具有重大社会冲力的非线性系统紊乱的漩涡将会使我们遭受灭顶之灾。但也未必,首先,语词“紊乱”已衍生出一种特定的科学意义,有些不同于(虽然并非不相容)它的日常用法。我在本文是指这个字的科学意义而言的。通常,不能外推出紊乱的经济或社会的消长比天气的变化无常更难以忍受。
其次也许有可能调节系统以制止它的紊乱行为,例如容易调节摆使它偏离紊乱状态。确实,虽然科学家们理解决定性的紊乱仅有几年时间,但未必以前没有人观测到表现出紊乱行为的简单物理系统。大多数人也许对于这类观测结果的反应是说:“有什么地方出毛病了”他们把紊乱看成是应该去排除而不是解释的东西。我已经提及可预见性的丧失与不稳定性之间的关联,并且我们知道我们能运用适当的反馈来消除不稳定性。也许将这类反馈应用于更复杂的和不定的社会系统比起应用于意义明确的物理系统要困难得多。然而,对决定性的紊乱基本概念的理解有能有助于这类应用。
[ New Scientist,1986年7月]